Пример расчета (задача № 19)

Определить главные напряжения и направления главных пло­щадок, если напряженное состояние в точке задано следующими компонентами: s_xx = 50 МПа, s_yy = -20 МПа, s_zz = 30 МПа, t_xy =
= -10 МПа, t_yz = 10 МПа, t_zx = 10 МПа.

Решение

1. В соответствии с (10.14) определяем инварианты заданного напряженного состояния:

I ₁ = s_xx + s_yy + s_zz = 50 - 20 + 30 = 60 МПа;

I ₂= s_xx s_yy + s_yy s_zz +s_xx s_zz - 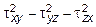= 50×(-20) +
+ (-20)×30 + 30×50 - 10² - 10² - 10² = -400 МПа.

I ₃=s_xx s_yy s_zz - =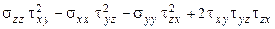
= 50×(-20)×30 -50×10² -(-20)×10² -30 -10² + 2×(-10)×10×10 =-38000 МПа.

2. Определяем коэффициенты уравнения (10.13). Если сделать

замену неизвестного S =s = x + 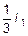, то из (10.13) получаем приве­денное уравнение:

,

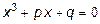где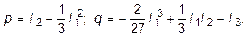

p = -400- 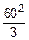=-1600, q = .

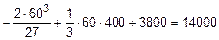Определим дискриминант приведенного уравнения:

.

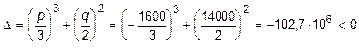Так как дискриминант отрицателен, значит все корни приве­денного уравнения вещественные.

3. Вычисление величин главных напряжений. Для решения приведенного уравнения применим формулу Кардано:

,

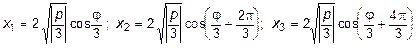где

cos j 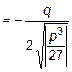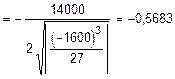®j = 124,63°;

cos (j/3) = cos (41,54°) = 0,7484; cos (j/3+2 p/3)=-0,9486; cos (j/3 + + 4 p/3) = 0,2;

;

.

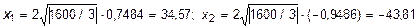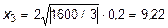Окончательно получим:

s₁ = 34,57 + 60/3 = 54,57 МПа;

s₂ = -43,81 + 60/3 = -23,8 МПа;

s₃ = 9,22 + 60/3 = 29,22 МПа.

Проверка правильности вычисления главных напряжений: так как I₁, I₂ и I₃ - инварианты, значит их значения постоянны. Ранее были получены их значения в заданной системе координат. Сейчас же найдем их значения в главной системе координат:

I₁ = s₁ + s₂ + s₃ = 54,57 - 23,8 + 29,22 = 59,99 МПа;

I₂= s₁ s₂ + s₁ s₃ + s₂ s₃ = 54,57×(-23,8) - 23,8×29,22 + 29,22×54,57 =
= -400,2 МПа;

I₃ = s₁ s₂ s₃ = 54,57×(-23,8)×29,22 = -37950 МПа.

Результаты вычислений I₁, I₂ и I₃ в рамках допустимых откло­нений совпадают с результатами, полученными в п. 1 решения.

4. Определяем направляющие косинусы главных площадок. Си­стема уравнений для определения l₁, m₁, n₁ имеет следующий вид:

(50 - 54,57) l₁ - 10 m₁ + 10 n₁ = 0;

-10 l₁ - (20 + 54,57) m₁ + 10 n₁ =0;

.

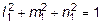Решение этой системы: l₁ = -0,9334; m₁ = 0,0785; n₁ = -0,3486. Условия проверки выполняются: (-0,9334)² +(-0,3486)² + 0,0785² @1.

Система уравнений для определения l₂, m₂, n₂ имеет следую­щий вид:

(50 + 23,81) l₂ -10 m₂ + 10 n₂ = 0;

-10 l₂ + (-20 + 23,81) m₂ + 10 n₂ =0;

.

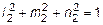Решение этой системы: l₂ = -0,159; m₂ = 0,965; n₂ = -0,2086. Условия проверки выполняются: 0,159² + 0,965² + (-0,2086)² @ 1.

Система уравнений для определения l₃, m₃, n₃ имеет следую­щий вид:

(50 - 29,22) l₃ - 10 m₃ + 10 n₃ = 0;

-10 l₃ + (-20 - 29,22) m₃ + 10 n₃ =0;

.

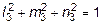Решение этой системы: l₃ = 0,5515; m₃ = 0,4328; n₃ = -0,7132. Условия проверки выполняются: 0,5515² + 0,4328² + (-0,7132)² @ 1.