Теория предельных напряженных состояний
При действии внешних сил материал конструкции может находиться в различных механических состояниях. При невысоких уровнях напряжений материал пребывает в упругом состоянии. При значительных напряжениях в материале обнаруживаются заметные остаточные деформации и он переходит в пластическое состояние. Затем, при дальнейшем увеличении внешних сил происходит образование местных трещин, и наступает его разрушение. Механическое состояние материала в точке зависит в первую очередь от напряженного состояния в ней. С целью определения прочности материалов вводится понятие предельное напряженное состояние.
Для пластичного материала предельным обычно считается, напряженное состояние, которое соответствует возникновению заметных остаточных деформаций, а для хрупкого - такое, при котором начинается разрушение материала.
Для выполнения расчетов на прочность вводятся понятия коэффициента запаса прочности и эффективное напряжение.
Коэффициент запаса при данном напряженном состоянии это число, показывающее во сколько раз следует одновременно увеличить все компоненты тензора напряжений, чтобы оно стало предельным.
Эквивалентное напряжение sЭКВ - это такое напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равно опасно с заданным.
Для пластичных материалов критерием наступления предельного состояния принимается состояние, при котором максимальные касательные напряжения достигают некоторого предельного значения:
sЭКВ = 2 tmax = s1 - s3 . (10.24)
Гипотеза максимальных касательных напряжений, приемлемая для пластичных материалов, обнаруживает заметные погрешности для материалов, имеющих различные механические характеристики при сжатии и растяжении.
В таких случаях применяется энергетическая гипотеза, согласно которой предельное состояние в точке наступает тогда, когда выражение
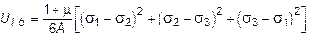(10.25)
принимает некоторое заранее заданное значение. Это предельное значение для UОФ определяется следующим образом. Для простого растяжения выражение (10.25) принимает вид:
.
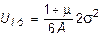В сложном напряженном состоянии UОФ принимает значение
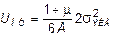. (10.26)
При совместном рассмотрении (10.25) и (10.26) получим:
sЭКВ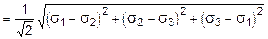 
или
sЭКВ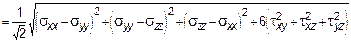 
Дата добавления: 2015-12-29; просмотров: 1367;