ОСНОВЫ ТЕОРИИ УПРУГОСТИ И ПЛАСТИЧНОСТИ

10.1. Напряженное состояние в точке.
Уравнения равновесия

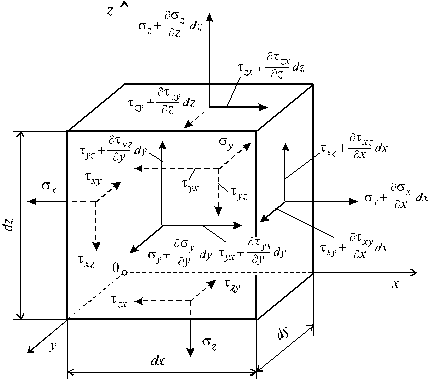
Чтобы охарактеризовать напряженное состояние в произволь­ной точке тела, находящегося в равновесном состоянии в общем случае нагружения, выделим в ее окре­стности некоторый объем в виде элементарного параллелепипеда, грани которого перпендикулярны координатным осям (рис. 10.1).

Если размеры параллелепипеда уменьшать, он будет стягивать­ся в эту точку. В пределе (dx, dy, dz ® 0) все грани параллелепипе­да пройдут через рассматриваемую точку и напряжения на соответ­ствующих плоскостях параллелепипеда могут рассматриваться как напряжения в исследуемой точке.

Полное напряжение, возникающее на площадке параллелепи­педа может быть разложено на три составляющие, одну по нормали к площадке и две в ее плоскости.

Рис. 10.1

Нормальное и касательное напряжение обозначаются через s и t, соответственно, с двумя индексами: s_xx , s_yy ,..., t_zx . Первый индекс соответствует координатной оси, перпендикулярной к пло­щадке на которой действует данное напряжение, а второй - оси, вдоль которой оно направлено. Поскольку, у нормальных напряже­ний оба индекса одинаковы, то для них применяют и одномерную индексацию: s_xx = s_x , s_yy = s_y , и s_zz = s_z . Ориентация осей является произвольной.

Правило знаков примем следующее: если внешняя нормаль к площадке совпадает по направлению с положительным направле­нием соответствующей оси, то напряжение считается положитель­ным, если оно направлено вдоль положительного направления оси, вдоль которой оно действует. Так, на рис. 10.1 все напряжения положительные.

Из трех условий равновесия параллелепипеда в виде суммы мо­ментов относительно координатных осей достаточно просто полу­чить важные утверждения, что

t_yz = t_zy ; t_zx = t_xz ; t_xy = t_yx . (10.1)

То есть, на двух взаимно перпендикулярных площадках состав­ляющие касательных напряжений, перпендикулярные к общему ребру, равны по величине и направлены обе либо к ребру, либо от него. Это утверждение - закон парности касательных на­пряжений, сформулированный в общем виде.

Рассматривая же равновесие параллелепипеда в виде суммы сил по направлениям координатных осей, и отбрасывая величины второго порядка ма­лости, легко получить дифференциальные уравнения его равнове­сия:

;

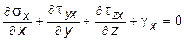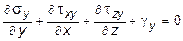; (10.2)

,

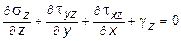где g_x , g_y , g_z - составляющие объемных сил вдоль координатных осей.

С учетом закона парности касательных напряжений (10.1), уравнения (10.2) содержат шесть неизвестных напряжений: s_x , s_y , s_z , t_xy , t_xz , t_yz . Поскольку количество уравнений равновесия ста­тики (10.2), меньше, чем количество неизвестных напряжений, то в общем случае задача определения напряженного состояния в произвольной точке сплошной среды нагруженного тела, является статически неопределимой.

Рис. 10.1

Нормальное и касательное напряжение обозначаются через s и t, соответственно, с двумя индексами: s_xx , s_yy ,..., t_zx . Первый индекс соответствует координатной оси, перпендикулярной к пло­щадке на которой действует данное напряжение, а второй - оси, вдоль которой оно направлено. Поскольку, у нормальных напряже­ний оба индекса одинаковы, то для них применяют и одномерную индексацию: s_xx = s_x , s_yy = s_y , и s_zz = s_z . Ориентация осей является произвольной.

Правило знаков примем следующее: если внешняя нормаль к площадке совпадает по направлению с положительным направле­нием соответствующей оси, то напряжение считается положитель­ным, если оно направлено вдоль положительного направления оси, вдоль которой оно действует. Так, на рис. 10.1 все напряжения положительные.

Из трех условий равновесия параллелепипеда в виде суммы мо­ментов относительно координатных осей достаточно просто полу­чить важные утверждения, что

t_yz = t_zy ; t_zx = t_xz ; t_xy = t_yx . (10.1)

То есть, на двух взаимно перпендикулярных площадках состав­ляющие касательных напряжений, перпендикулярные к общему ребру, равны по величине и направлены обе либо к ребру, либо от него. Это утверждение - закон парности касательных на­пряжений, сформулированный в общем виде.

Рассматривая же равновесие параллелепипеда в виде суммы сил по направлениям координатных осей, и отбрасывая величины второго порядка ма­лости, легко получить дифференциальные уравнения его равнове­сия:

;

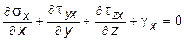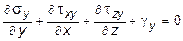; (10.2)

,

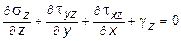где g_x , g_y , g_z - составляющие объемных сил вдоль координатных осей.

С учетом закона парности касательных напряжений (10.1), уравнения (10.2) содержат шесть неизвестных напряжений: s_x , s_y , s_z , t_xy , t_xz , t_yz . Поскольку количество уравнений равновесия ста­тики (10.2), меньше, чем количество неизвестных напряжений, то в общем случае задача определения напряженного состояния в произвольной точке сплошной среды нагруженного тела, является статически неопределимой.