Запас усталостной прочности и его определение

Сначала построим диаграмму усталостной прочности (часто, для простоты рассуждений предельную линию представляют в виде прямой) и покажем на ней рабочую точку М цикла (с коорди­натами s_m и s_а ) в случае, если рассматриваемый элемент испыты­вает только простое растяжение и сжатие (рис. 9.7).

Рассмотрим все те циклы, рабочие точки которых лежат на од­ной прямой (рис. 9.7) и для которых справедливо выражение s_а = = s_m tga. С учетом (9.1) и после несложных преобразований можно получить, что:

.

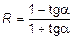где R - коэффициент асимметрии цикла.

Значит, можно сделать вывод о том, что все подобные циклы лежат на одной прямой. Тогда, под запасом усталостной прочности будем понимать отношение отрезка ON к отрезку OM (рис. 9.7):

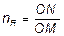, (9.6)

где точка M соответствует действующему циклу, а точка N получа­ется вследствие пересечения предельной прямой и продолжения отрезка OM (рис. 9.7).

Это отношение характеризует степень близости рабочих усло­вий к предельным для данного материала. В частном случае при постоянных статических нагрузках s_а = 0, данное определение за­паса прочности совпадает с обычным.

Рис. 9.7

Для определения 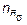(т.е. в ситуации когда действуют лишь нор­мальные напряжения) в инженерной практике применяется как графи­ческий, так и аналити­ческий способ. При гра­фическом способе стро­го по масштабу строится диаграмма предельных напряжений в системе координат s_а и s_m . Да­лее, на этой диаграмме наносится рабочая точка и определяется отношение величин отрезка ON и OM. Для определения расчетных зависимостей для 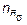воспользуемся условием подобия треуголь­ников OND и OMK и получим:

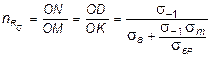. (9.7)

Полученный коэффициент запаса соответствует идеальному об­разцу. Реальная же его величина зависит, как отмечалось выше, от геометрии, размеров и состояния поверхности образца, учитывае­мых коэффициентами К_-1, e_s и b, соответственно. Для этого необ­ходимо предел усталости при симметричном нагружении умень­шить в 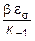раз, или, что тоже самое, амплитудное напряжение цикла увеличить в 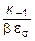раз. И тогда (9.7) принимает вид:

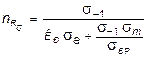, (9.8)

где

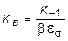. (9.9)

Аналогичным образом могут быть получены соотношения уста­лостной прочности и при чистом сдвиге. Эксперименты показы­вают, что диаграмма усталостной прочности для сдвига заметно отличается от прямой линии, свойственной простому растяжению-сжатию, и имеет вид кривой. В первом приближении эту кривую в координатных осях t_a , t_m можно представить в виде двух наклон­ных, как это изображено на рис. 9.8. Причем, если одна из них (ближняя к оси ординат) соответствует разрушению образца вследствие усталостных явлений, то другая - по причине наступления пластического состояния.

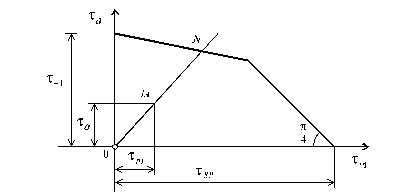
Рис. 9.8

В данном случае расчетная формула для 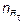записывается в виде

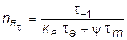, (9.10)

где 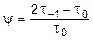- эмпирическая величина, определенная на осно­ве обработки экспериментальных данных.

При сложном напряженном состоянии, т.е. если в рабочей точ­ке при действии внешних нагрузок одновременно возникают как нормальные, так и касательные напряжения, для вычисления n_R применяется следующая приближенная формула:

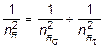, (9.11)

где n_R - искомый коэффициент запаса усталостной прочности; 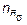- коэффициент запаса усталостной прочности в предположе­нии, что касательные напряжения в рабочей точке отсутствуют; 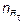- коэффициент запаса прочности по усталости при предполо­жении, что в рабочей точке нормальные напряжения отсутствуют.

Резюмируя заметим, как это было показано в настоящем раз­деле книги, в настоящее время в связи с тем, что физические осно­вы теории твердого деформируемого тела недостаточно развиты, многие предпосылки современной теории усталостной прочности базируются на эмпирической основе. Отсутствие твердых предпо­сылок в теории выносливости, в современном виде лишает ее нуж­ной строгости. Так как полученные эмпирические зависимости не являются универсальными, сами результаты расчетов являются до­статочно приближенными. Однако указанные приближения оказы­ваются допустимыми для решения инженерных задач.