ДЕЙСТВУЮЩАЯ НА ПЛОСКУЮ ФИГУРУ ЛЮБОЙ ФОРМЫ

Представим на рис. 2-15, а открытый сосуд, наполненный жидкостью и имеющий плоскую наклонную стенку ОМ. В плоскости этой стенки наметим оси координат Oz и Ох. Ось Ох направим перпендикулярно к плоскости чертежа.

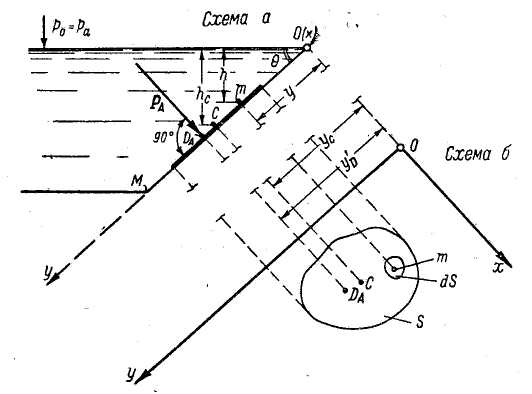
Рис. 2-15. Давление жидкости на плоскую наклонную фигуру площадью S

На стенке сосуда ОМ наметим некоторую плоскую фигуру любого очертания, имеющую площадь S. Эта фигура на рис. 2-15,а будет проектироваться в линию (показанную на чертеже жирно). Представим еще на рис. 2-15, б стенку сосуда ОМ, повернутую относительно оси Oz на 90° (совмещенную с плоскостью чертежа). Ясно, что на рис. 2-15, б намеченная плоская фигура будет изображаться без искажения.

В соответствии с первым свойством гидростатического давления (см. § 2-2) можем утверждать, что во всех точках площади S давление жидкости будет направлено нормально к стенке. Отсюда заключаем, что сила абсолютного гидростатического давления P_A, действующая на произвольную плоскую фигуру площадью S, будет также направлена по отношению к стенке нормально (как это показано на рис. 2-15, а).

Поставим перед собой цель найти:

а) силу P_A абсолютного гидростатического давления;

б) положение линии действия силы P_A.

1. Сила P_A. Наметим на рассматриваемой фигуре произвольную точку т, заглубленную под уровнем жидкости на h и имеющую координату z; ясно, что

h = zsinθ, (2-75)

где θ - угол наклона боковой стенки сосуда к горизонту.

У точки т выделим элементарную площадку dS. Сила абсолютного гидростатического давления, действующая на эту площадку,

dP_A = p_AdS, (2-76)

или, согласно (2-40),

dP_A = (p_a + γh)dS = p_adS + γhdS = p_adS + γzsinθdS. (2-77)

Интегрируя это выражение по всей площади S, получаем:

P_A = p_a 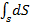+ γsinθ 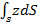. (2-78)

Ясно, что:

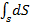= S; = (S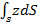t)_ox = z_cS, (2-79)

где (St)_ox - статический момент плоской фигуры относительно оси Ox; z_c - координата центра тяжести (точки С) данной плоской фигуры. Подставляя (2-79) в (2-78), получаем:

P_A = p_aS + γSz_csinθ. (2-80)

Так как

z_csinθ = h_c,

где h_c - заглубление центра тяжести С плоской фигуры под горизонтом жидкости, то

P_A = p_aS + γh_cS (2-81)

или

(2-82)

где (p_A)_c - абсолютное гидростатическое давление в точке, являющейся центром тяжести рассматриваемой плоской фигуры.

Формулу (2-81) можно представить еще в виде:

P_A = P_a + P, (2-83)

здесь P_a - сила, обусловленная атмосферным (поверхностным) давлением, передающимся через жидкость на плоскую фигуру:

P_a = p_aS; (2-84)

P - сила избыточного в данном случае весового давления:

P = γh_cS = p_cS, (2-85)

где p_c - избыточное (весовое) давление в центре тяжести фигуры.

Как видно, сила гидростатического давления (абсолютного или избыточного), действующая на плоскую фигуру любой формы, равна площади этой фигуры, умноженной на соответствующее гидростатическое давление [(p_A)_c или p_c] в центре тяжести этой фигуры.

Точка D_A пересечения линии действия силы P_A с плоскостью, в которой лежит рассматриваемая фигура, называется центром давления силы P_A. Найдем положение точки D_A; этим и определится линия действия силы P_A.

2. Положение центра давления. Представим на рис. 2-16 деталь предыдущего чертежа. Центр давления силы P_a будет совпадать с центром тяжести фигуры, так как поверхностное давление p₀ = p_a, передаваясь через жидкость, равномерно распределяется по рассматриваемой площади. Что касается избыточного давления, то оно распределяется неравномерно по площади фигуры: чем глубже расположена точка фигуры, тем большее давление она испытывает; поэтому центр давления силы Р будет лежать ниже центра тяжести фигуры (см. точку D).

Искомая сила P_A является геометрической суммой сил P_a и Р. Точка D_A будет лежать между точками С и D; эта точка D_A найдется в результате геометрического сложения сил Р_а и Р. Таким образом, вопрос сводится к отысканию точки D, определяемой координатой z_D. Зная z_D, мы далее, как указано выше, найдем и величину z'_D, определяющую положение точки D_A.

Расчетную зависимость для величины z_D находят, исходя из следующего условия: сумма моментов составляющих элементарных сил pdS относительно оси Ох равна моменту равнодействующей силы Р относительно той же оси Ох.

Имея в виду это условие, можем написать:

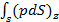= Pz_D. (2-86)

Эту формулу можно переписать в виде

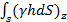= (γh_cS)z_D

или

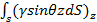= (γh_cS)z_D,

Откуда

z_D = 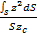= 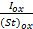(2-87)

где

I_ox = 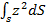(2-88)

момент инерции плоской фигуры относительно оси Ох, а

(St)_ox = Sz_c (2-89)

есть, как это уже отмечалось, статический момент плоской фигуры относительно оси Ох.

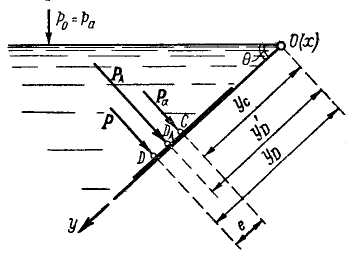
Рис. 2-16. Центр силы гидростатического давления

С - центр тяжести фигуры, D_А – центр давления силы Р_А, D - центр давления силы Р, е - эксцентриситет силы Р

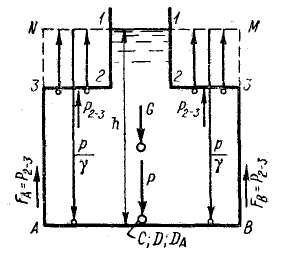
Рис. 2-17. Гидростатическое давление на дно сосуда, наполненного жидкостью

F_А и F_B - усилия, передающиеся дну вертикальными стенками сосуда

Формулу (2-87) можно еще переписать в виде

z_D = 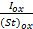= = 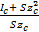z_c + 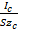(2-90)

или

z_D = z_C + e, (2-91)

где положительная величина е называется эксцентриситетом. Эксцентриситет

e = 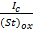= 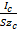(2-92)

причем здесь I_c есть момент инерции рассматриваемой плоской фигуры относительно горизонтальной оси, проходящей через центр тяжести фигуры. Как видно, центр давления силы Р лежит ниже центра тяжести фигуры на величину, равную е.

Выше мы ограничились отысканием только одной координаты точки D (координаты z_D). Однако в общем случае приходится еще определять и вторую координату (x_D). Ее можно найти, исходя из уравнения моментов соответствующих сил [уравнения, аналогичного (2-86)] относительно оси Oz.

3. Случай горизонтальной плоской фигуры. В заключение рассмотрим частный случай - случай плоской фигуры, расположенной горизонтально (см. АВ на рис. 2-17). Как видно, в этом частном случае избыточное гидростатическое давление р, выражаемое заглублением точек плоского дна АВ под уровнем жидкости 3-4, будет распределяться равномерно по всей плоскости АВ. Поэтому в данном случае e =0 и центры давления D_A и D должны совпадать с центром тяжести С. Величина силы избыточного давления Р, действующего на горизонтальное дно сосуда, показанного на рис. 2-17, будет выражаться эпюрой ANMB (весом жидкости в объеме ANMB).

Представим себе, что рассматриваемый сосуд поставлен на весы. Ясно, что на весы будет передаваться вес G жидкости, находящейся в сосуде, выражаемый площадью эпюры А-1-2-3-4-5-6-В (весом стенок сосуда пренебрегаем). Вместе с тем, как это было указано выше, на дно сосуда АВ действует сила Р давления жидкости, выражаемая площадью ANMB, причем эта площадь может значительно отличаться по величине от площади А-1-2-3-4-5-6-В.

Как видно, надо различать две разные силы: а) силу Р давления жидкости на дно; б) силу G давления дна на весы, причем в общем случае

P 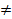G

Такое положение объясняется следующим.

Силы P_1-2 и P_5-6 (рис 2-17) вертикального давления жидкости на стенки 1-2 и 5-6 выражаются эпюрами 1-2-3-N и 4-5-6-М. Эти силы передаются через стенки сосуда на дно АВ сосуда:

F_A = P_1-2; F_B = P_5-6

следовательно,

G = P – F_A - F_B.