СИЛА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ, ДЕЙСТВУЮЩАЯ НА ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
В практике приходится определять силу гидростатического давления не только на плоские поверхности, но и на поверхности криволинейные любого вида. Ниже рассмотрим только простейший частный случай криволинейной поверхности - цилиндрическую поверхность, которая встречается наиболее часто.
Будем рассматривать только избыточное давление, вовсе не интересуясь поверхностным давлением.
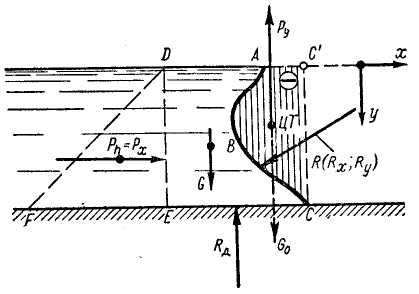
Рис. 2-20. Давление на цилиндрическую поверхность ABC (вертикаль С-С' лежит вне жидкости)
1-й случай цилиндрической поверхности. Представим на рис. 2-20 цилиндрическую поверхность ABC. Эта поверхность расположена перпендикулярно к плоскости чертежа, и потому она проектируется в одну линию ABC (кривая ABC есть направляющая рассматриваемой цилиндрической поверхности). Обозначим длину образующей цилиндрической поверхности, перпендикулярной к плоскости чертежа, через b (b=const). Наметим вертикальную плоскость СС' и оси координат х и z. Обозначим через Рх и Pz горизонтальную и вертикальную составляющие силы Р гидростатического давления, действующего со стороны жидкости на цилиндрическую поверхность.
Обратимся вначале к отысканию составляющих Рх и Pz искомой силы Р. С этой целью проведем вертикальную плоскость DE. Плоскость DE выделит объем покоящейся жидкости ABCED, равновесие которого далее рассматриваем. На этот объем действуют следующие силы:
1) сила Ph, действующая на вертикальную грань DE со стороны жидкости, расположенной слева от этой грани;
2) сила Rд - со стороны дна ЕС (реакция дна; см. конец § 2-10):
RД = [площадь(C’CED)]bγ; (2-98)
3) реакция R - со стороны цилиндрической поверхности; горизонтальную и вертикальную составляющие этой реакции обозначим соответственно Rх и Rz; значения и направления этих сил (в отличие от других) нам неизвестны;
4) собственный вес G рассматриваемого объема жидкости:
G = [площадь(ABCED)]bγ. (2-99)
Проектируя все силы, действующие на покоящийся объем ABCDE, соответственно на оси х и z, получаем следующие уравнения равновесия [не зная направления Rх и Rz, вводим их в уравнения (2-100) со знаком плюс]:
Ph + Rx = 0; G + Rz – RД = 0, (2-100)
откуда
Rx = - Ph; Rz = RД - G. (2-101)
Так как силы Рх и Pz направлены противоположно силам Rх и Rz, то можем написать:
Px = -Rx и Pz = - Rz, (2-102)
при этом вместо (2-101) имеем:
| Px = Ph; |
(2-103)
Pz = - (Rд – G). (2-104)
Далее преобразуем уравнение (2-104); подставляя в него (2-98) и (2-99), получаем:
Pz = - [площадь(C’CDE) – площадь(ABCED)]bγ (2-105)
или
| Pz = - [площадь(ABCC’)]bγ |
(2-106)
Рассмотрев (2-103) и (2-106), можно заключить следующее.
1. Горизонтальная составляющая Рх искомой силы равна силе давления жидкости на плоскую вертикальную прямоугольную фигуру DE, представляющую собой проекцию рассматриваемой цилиндрической поверхности на вертикальную плоскость. В связи с этим сила Рх=Ph может быть выражена, как и в случае плоских фигур, треугольником гидростатического давления DEF.
2. Вертикальная составляющая Pz искомой силы равна взятому со знаком минус весу воображаемого жидкого тела площадью сечения АВСС'. Это воображаемое жидкое тело называется телом давления(см. площадь, покрытую на чертеже штриховкой).
Обозначим вес тела давления через Go. Тогда вместо (2-106) можно написать
| Pz = - G0 |
(2-107)
Найдя таким образом составляющие Рх и Pz, путем геометрического сложения их определяем искомую силу Р давления жидкости на рассматриваемую цилиндрическую поверхность.
Как видно, 1-й случай цилиндрической поверхности характеризуется тем, что вертикаль СС' лежит вне жидкости.
2-й случай цилиндрической поверхности (вертикаль СС' лежит внутри жидкости). Представим на рис. 2-21 случай, когда жидкость находится над цилиндрической поверхностью. Ограничимся здесь отысканием только составляющих Рх и Pz. Рассуждая, как и выше, можно показать, что горизонтальная составляющая Рх выражается точно так же, как и в предыдущем случае. Что же касается составляющей Pz, то оказывается, что для цилиндрической поверхности, показанной на рис. 2-21,
| Pz = + G0 |
(2-108)
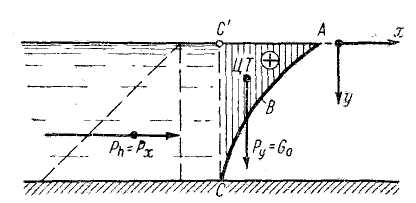
Рис. 2-21. Эпюры давления на цилиндрическую поверхность ABC (вертикаль С-С' лежит внутри жидкости)
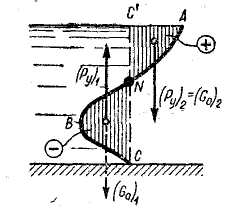
Рис. 2-22. Эпюра вертикального давления (тела давления) на цилиндрическую поверхность ANВС
(вертикаль С-С' частично лежит вне жидкости, частично - внутри жидкости)
Как видно, в данном случае «тело давления» (см. заштрихованную площадь на рис. 2-21) лежит в области действительной, а не воображаемой жидкости. Имея это в виду, такое тело давления называют положительным; тело же давления в первом случае цилиндрической поверхности называют отрицательным.
3-й случай цилиндрической поверхности. Представим на рис. 2-22 такую цилиндрическую поверхность ABC, которая пересекается в некоторой «узловой точке» N с вертикалью СС', проведенной через нижнюю точку С цилиндрической поверхности. Как видно, в данном случае одновременно получаем и положительное и отрицательное тела давления. Складывая силы (Pz)1, (Pz)2 и Рх (определенные, как указано выше), находим искомую силу Р.
4-й случай цилиндрической поверхности. Плоский прямоугольник, проектирующийся в линию ABC (рис. 2-23), является частным случаем цилиндрической поверхности. Поэтому при отыскании Р для этого прямоугольника можно поступить так же, как во втором случае цилиндрической поверхности. В результате найдем составляющие Рх и Pz. Складывая геометрически эти две силы, получим силу, выражаемую эпюрой ОА'В, представленной на рис. 2-19, б.
Заключительное замечание. При построении поперечного сечения тела давления, т. е. эпюры, выражающей вертикальную составляющую Pz, в общем случае можно поступать следующим образом.
Имеем цилиндрическую поверхность ABC, для которой следует построить тело давления (рис. 2-24); при этом прежде всего фиксируем крайние точки А и С этой поверхности; далее от этих точек проводим вверх вертикали до горизонта жидкости или его продолжения; наконец, намечаем контур тела давления, причем руководствуемся правилом:
поперечное сечение тела давления (отрицательного или положительного) представляет собой фигуру, заключенную между указанными вертикалями, самой цилиндрической поверхностью ABC и горизонтом жидкости (или его продолжением). Если рассматриваемая цилиндрическая поверхность со стороны тела давления не смачивается жидкостью, то имеем отрицательное тело давления (рис. 2-24); в противном случае - положительное тело давления.
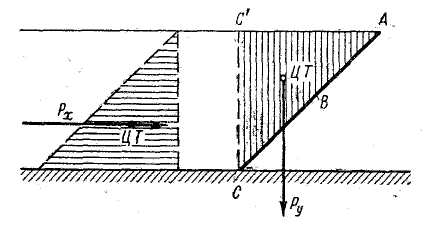
Рис. 2-23. Эпюры составляющих сил давления на плоскую прямоугольную фигуру
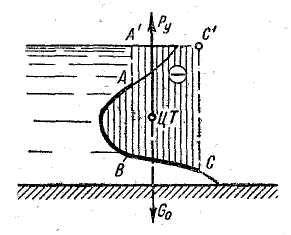
Рис 2-24. Построение поперечного сечения тела давления для цилиндрической поверхности ABC
Обратим еще внимание на то, что сила гидростатического давления Р для криволинейной (цилиндрической) поверхности, в отличие от силы Р, действующей на плоскую поверхность, не может быть представлена площадью только одной эпюры давления; выше мы представляли эту силу (в общем случае цилиндрической поверхности) двумя эпюрами -для Рх и Рг.
Дата добавления: 2015-12-29; просмотров: 3533;
