VIII. Гиперповерхности и поверхности второго порядка

Понятия поверхности и линии (кривой) относятся к фундаментальным понятиям геометрии (топологии); используются практически во всех математических и естественных науках. Поэтому их общее определение довольно затруднительно. 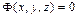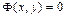В геометрии, аналитической и алгебраической, поверхность и линия определяются как геометрическое место точек, координаты которых записаны в декартовых координатах и удовлетворят уравнению или , соответственно.

В n-мерных линейных пространствах плоскость размерности (n-1) называется гиперплоскостью, а плоскость размерности 1 – прямой линией. Аналогичную терминологию будем применять и к поверхностям. Учитывая геометричность многих свойств поверхности и гиперповерхности, в дальнейшем будем называть векторы точками пространства действительных чисел 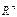. Это подтверждается и эквивалентностью понятий n-мерного векторного пространства и пространства 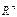[4].

Зададим в пространстве 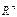декартовую систему координат и превратим его в евклидово, то есть определим в 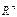скалярное произведение.

Определение. Гиперповерхностью f второго порядка в 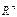называется множество точек 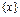, координаты 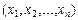которых удовлетворяют уравнению

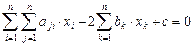, (VIII.1)

, .

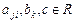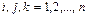Формулу (VIII.1) можно упростить, если определить скалярное произведение в 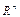как сумму попарных произведений координат, тогда получим

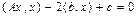. (VIII.2)

Учитывая симметричность матрицы A линейного оператора, имеем также для (VIII.1)

.

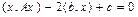Для исследования гиперповерхности (VIII.1) удобно преобразовать ее к каноническому виду. Воспользуемся уравнением (VIII.2). Процесс приведения к каноническому виду происходит в полном соответствии с алгоритмом приведения к каноническому виду квадратичных форм [7], которые нами уже изучены.