VII. Билинейные и квадратичные формы
Билинейные формы
|
|
|
|
|
|
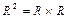 по двум координатным осям. Следовательно, плоскость можно рассматривать как множество значений скалярной (вещественной) функции двух аргументов,
по двум координатным осям. Следовательно, плоскость можно рассматривать как множество значений скалярной (вещественной) функции двух аргументов, 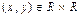 .
.
Пусть M и N линейные пространства и L их прямая сумма 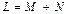 (напомним, что
(напомним, что 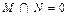 ) над одним и тем же скалярным полем (полем R) [11].
) над одним и тем же скалярным полем (полем R) [11].
Определение. Действительная функция j, заданная на линейном пространстве L, называется билинейной формой (билинейным функционалом), если равенства
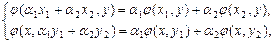 (VII.1)
(VII.1)
тождественно выполняются для всех ее аргументов и скаляров.
Формула (VII.1) представляет множество функций двух аргументов, у которых фиксированное значение одного из аргументов линейно зависит от другого.
Линейность билинейной формы легко проверяется, поэтому множество билинейных форм образует линейное пространство; нулем будет форма 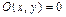 , называемая нулевой формой.
, называемая нулевой формой.
Отметим два свойства билинейных форм:
1) если n-мерное линейное пространство 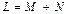 – прямая сумма линейных пространств M и N с размерностями k и m, то для любого множества действительных чисел вида
– прямая сумма линейных пространств M и N с размерностями k и m, то для любого множества действительных чисел вида 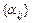 ,
, 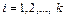 ,
, 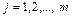 существует, и при том единственная, билинейная форма, такая, что
существует, и при том единственная, билинейная форма, такая, что 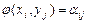 ;
;
2) размерность r пространства всех билинейных форм равна произведению размерностей M и N, то есть 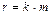 .
.
Пример VII.1. В Евклидовом пространстве скалярное произведение является билинейной формой. ▼
Пусть L – n-мерное линейное пространство и 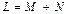 с размерностью k и m, соответственно. Если
с размерностью k и m, соответственно. Если 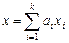 ,
, 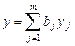 , где
, где 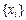 ,
, 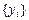 – базисы линейных пространств m и N, соответственно, то из формулы (VII.1) и свойства 1 имеем
– базисы линейных пространств m и N, соответственно, то из формулы (VII.1) и свойства 1 имеем
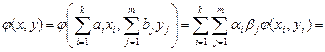
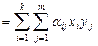 . (VII.2)
. (VII.2)
В дальнейшем нас будет интересовать билинейная форма, аргументы которой совпадают, то есть 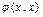 .
.
Квадратичные формы
Определение. Билинейная форма 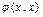 одного векторного аргумента x называется квадратичной.
одного векторного аргумента x называется квадратичной.
Пусть L – n-мерное линейное вещественное пространство и 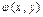 – билинейная форма, тогда квадратичная форма
– билинейная форма, тогда квадратичная форма 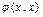 , как следует из (VII.2), имеет вид
, как следует из (VII.2), имеет вид
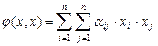 , (VII.3)
, (VII.3)
где коэффициенты при 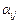 как-то выражены через
как-то выражены через 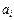 ,
, 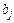 .
.
Если в (VII.3) привести подобные члены, то при 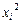 получим коэффициент
получим коэффициент 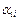 , а коэффициенты при
, а коэффициенты при 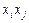 обозначим через
обозначим через 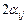 , тогда можно составить матрицу
, тогда можно составить матрицу 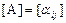 , которая называется матрицей квадратичной формы, а ее ранг r называется рангом квадратичной формы.
, которая называется матрицей квадратичной формы, а ее ранг r называется рангом квадратичной формы.
Матрица 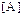 симметрическая. Ее характеристикой является совпадение со своей транспонированной матрицей.
симметрическая. Ее характеристикой является совпадение со своей транспонированной матрицей.
Так как L вещественное, то в нем можно ввести скалярное произведение как сумму парных произведений координат. Тогда формулу (VII.3) можно упростить. В самом деле, составим матрицу 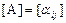 и введем пространство
и введем пространство 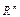 , элементами которого являются вектор – столбцы, то есть
, элементами которого являются вектор – столбцы, то есть 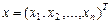 . Учитывая введенное скалярное произведение, положим
. Учитывая введенное скалярное произведение, положим
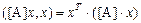 . (VII.4)
. (VII.4)
В силу симметричности матрицы 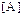
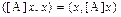 .
.
Пример VII.2. Пусть 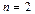 , тогда в
, тогда в 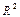 имеем
имеем 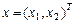 ,
, 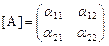 ,
, 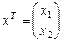 . Учитывая (VII.4), получаем
. Учитывая (VII.4), получаем
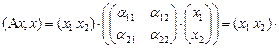
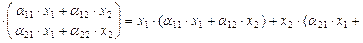
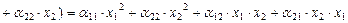 .
.
Дата добавления: 2016-01-26; просмотров: 1404;
