Классификация поверхностей второго порядка
II. Рассмотрим в 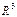 поверхность 2-го порядка, которая имеет размерность
поверхность 2-го порядка, которая имеет размерность 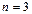 [9, 10].
[9, 10].
Определение. Поверхностью 2-го порядка в декартовой системе координат 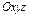 пространства
пространства 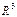 называется множество точек, удовлетворяющих уравнению вида
называется множество точек, удовлетворяющих уравнению вида
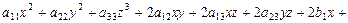
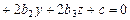 . (VIII.5)
. (VIII.5)
Линейным преобразованием (матрицей линейного оператора) уравнение (VIII.5) приводится к одному из пяти линейно независимых уравнения канонического вида
1) 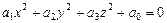 ,
,
2) 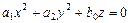 ,
,
3) 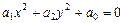 , (VIII.6)
, (VIII.6)
4) 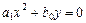 ,
,
5) 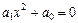 ,
,
где коэффициенты во всех уравнениях не равны 0.
Как и ранее, выделим классы поверхностей:
· невырожденные и нераспадающиеся поверхности:
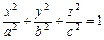 - эллипсоид (рис. VIII.5);
- эллипсоид (рис. VIII.5);
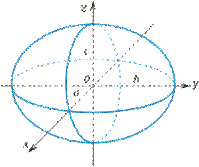
Рис. VIII.5
Если 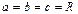 , то эллипсоид становится сферой
, то эллипсоид становится сферой
(рис. VIII.6);
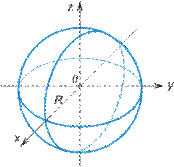
Рис. VIII.6
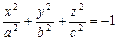 - мнимый эллипсоид;
- мнимый эллипсоид;
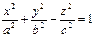 - однополостной гиперболоид (рис. VIII.7);
- однополостной гиперболоид (рис. VIII.7);

Рис. VIII.7
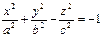 - двуполостной гиперболоид (рис. VIII.8);
- двуполостной гиперболоид (рис. VIII.8);
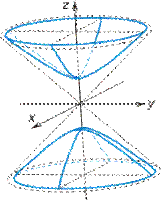
Рис. VIII.8
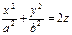 ,
, 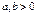 - эллиптический параболоид (рис. VIII.9);
- эллиптический параболоид (рис. VIII.9);
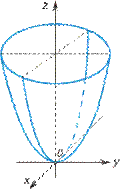
Рис. VIII.9
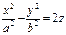 ,
, 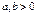 - гиперболический параболоид (рис. VIII.10);
- гиперболический параболоид (рис. VIII.10);
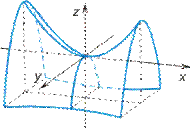
Рис. VIII.10
· вырождающиеся нераспадающиеся поверхности:
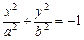 - мнимый эллиптический цилиндр;
- мнимый эллиптический цилиндр;
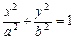 - эллиптический цилиндр (рис. VIII.11);
- эллиптический цилиндр (рис. VIII.11);
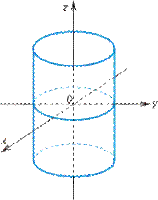
Рис. VIII.11
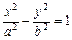 - гиперболический цилиндр (рис. VIII.12);
- гиперболический цилиндр (рис. VIII.12);
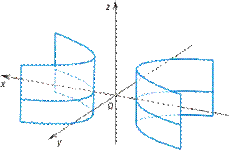
Рис. VIII.12
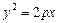 - параболический цилиндр (рис. VIII.13);
- параболический цилиндр (рис. VIII.13);
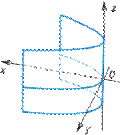
Рис. VIII.13
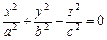 - коническая поверхность (рис. VIII.14);
- коническая поверхность (рис. VIII.14);
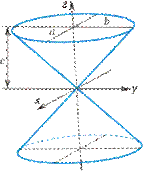
Рис. VIII.14
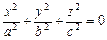 - мнимая коническая поверхность;
- мнимая коническая поверхность;
· вырождающиеся распадающиеся поверхности:
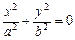 - пара мнимых пересекающихся плоскостей;
- пара мнимых пересекающихся плоскостей;
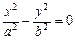 - пара пересекающихся прямых;
- пара пересекающихся прямых;
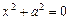 - пара мнимых параллельных плоскостей;
- пара мнимых параллельных плоскостей;
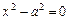 - пара параллельных плоскостей;
- пара параллельных плоскостей;
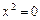 - пара совпадающих плоскостей.
- пара совпадающих плоскостей.
Пример VIII.4. Преобразовать к каноническому виду поверхность 2-го порядка
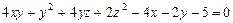 .
.
Решение. Прежде чем переходить к повороту осей координат  , осуществим линейный перенос так, чтобы можно было применить методику квадратичных форм. Положим
, осуществим линейный перенос так, чтобы можно было применить методику квадратичных форм. Положим
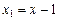 ,
, 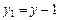 ,
, 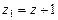 ,
,
тогда поверхность запишется в виде
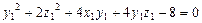 .
.
Рассмотрим квадратичную форму
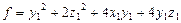 .
.
Составим матрицу квадратичной формы
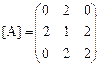 .
.
Найдем собственные числа и собственные векторы. Имеем характеристический многочлен:
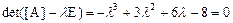 ,
,
корни которого 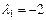 ,
, 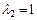 ,
, 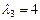 .
.
Запишем канонический вид поверхности с точностью до коэффициентов (сначала запишем их положительные значения):
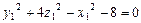 .
.
По классификации это однополостной гиперболоид. Явный вид линейного преобразования находим аналогично примерам предыдущего раздела:
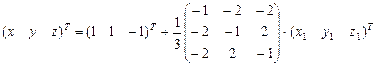 ,
,
где первое слагаемое определяет параллельный сдвиг, а второе поворот вокруг оси симметрии. Окончательно
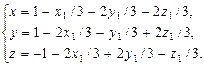
Дата добавления: 2016-01-26; просмотров: 1381;
