СИЛА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ, ДЕЙСТВУЮЩАЯ НА ПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ ФИГУРЫ

Возьмем плоскую вертикальную фигуру ОА (рис. 2-18, а), имеющую горизонтальное основание; ширину этого прямоугольника обозначим через b (рис. 2-18,6). Будем рассматривать только избыточное давление на эту фигуру; поверхностное давление, которое часто равно атмосферному, учитывать не будем. Заметим, что при статическом расчете стенки ОА нам приходится учитывать только избыточное давление, так как атмосферное давление, которое передается через жидкость и действует на стенку слева, полностью уравновешивается атмосферным давлением, действующим непосредственно на стенку справа.

Наметим на поверхности фигуры ОА точку т. Давление в этой точке будет

p = γh. (2-93)

Представим себе, что точка т перемещается от О до А по прямой линии; при этом, как видно из (2-93), гидростатическое давление будет изменяться по линейному закону. Для точки О при h=0

p= 0; (2-94)

для точки А

p = γh_1, (2-95)

где h₁ - «глубина воды» (или любой жидкости) перед плоской фигурой (заглубление точки А под свободной поверхностью жидкости).

Учитывая приведенные соотношения, отложим на рис. 2-18, а перпендикулярно поверхности ОА отрезок γh₁ причем получим точку В. Соединим теперь точку О и точку В прямой линией. В результате получим треугольник ОАВ. Этот треугольник называется эпюрой гидростатического давления.

Площадь треугольника ОАВ, умноженная на ширину b, дает нам силу Р гидростатического давления, действующего на прямоугольную фигуру:

P = Ωb = 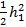γb. (2-96)

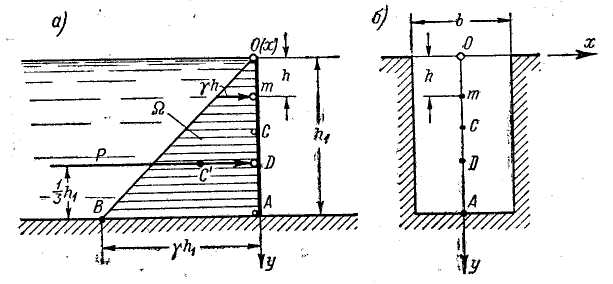
Рис. 2-18. Одностороннее гидростатическое давление на вертикальную плоскую фигуру прямоугольной формы

D - центр давления; С - центр тяжести плоской фигуры; С’ - центр тяжести эпюры давления

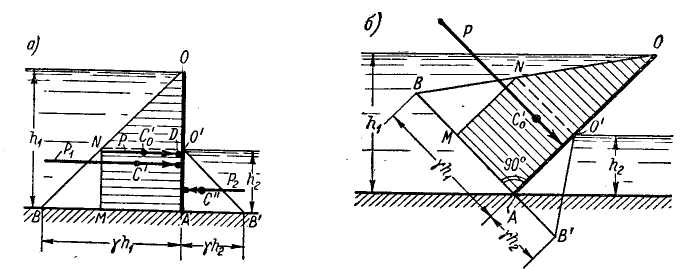
Рис. 2-19. Эпюры давления на плоские прямоугольные фигуры:

а - вертикальная фигура; б - наклонная фигура

Сила Р должна быть перпендикулярна к линии ОА и проходить через центр тяжести С' эпюры давления. Отсюда заключаем, что центр давления силы Р (точка D) должен располагаться на расстоянии h₁ от дна прямоугольного лотка, в котором установлен рассматриваемый вертикальный прямоугольный щит.

Иногда при построении эпюры давления по перпендикуляру от точки А откладывают не γh₁ как это мы делали выше, a h₁. При таком построении эпюры давления вместо формулы (2-96) будем иметь:

P = Ωbγ = 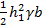. (2-97)

Надо помнить, что эпюра гидростатического давления характеризуется следующими двумя свойствами:

1) каждая ордината эпюры давления, измеренная перпендикулярно к щиту ОА, выражает заглубление соответствующей точки щита, а следовательно, и гидростатическое давление в этой точке;

2) площадь эпюры давления выражает силу Р гидростатического давления (суммарное гидростатическое давление).

При наличии воды с двух сторон рассматриваемого щита ОА (рис. 2-19, а) приходится строить отдельно две эпюры давления (два треугольника гидростатического давления): для жидкости, находящейся слева от щита (см. треугольник ОАВ), и для жидкости, находящейся справа от щита (см. треугольник О'АВ'). После этого два полученных треугольника складываем, как показано на чертеже; в результате получаем эпюру давления в виде трапеции OAMN. Очевидно, площадь этой трапеции будет выражать искомую силу Р; линия действия силы Р должна проходить через центр тяжести С'о трапеции перпендикулярно к щиту ОА.

В случае наклонного прямоугольного щита окончательная эпюра давления, учитывающая давление воды слева и справа на щит, будет иметь вид трапеции OAMN, показанной на рис. 2-19, б.