Декартовы прямоугольные координаты
Положение точки в пространстве будем определять относительно пространственной декартовой прямоугольной системы координат, состоящей из трех взаимно перпендикулярных осей координат, пересекающихся в одной точке О, называемой началом координат.
Ось Ox называют осью абсцисс, ось Oy - осью ординат и ось Oz - осью аппликат.
Координатные оси Ox, Oy, Oz, взятые попарно, определяют три взаимно перпендикулярные плоскости xOy, yOz, xOz, называемые координатными плоскостями.
Декартова система координат позволяет связать с каждой точкой P пространства, в котором выбраны три не лежащие в одной плоскости направленные прямые Ox, Oy, Oz (оси координат), пересекающиеся в начале O, три вполне определенных действительных числа (декартовы координаты) x, y, z; при этом пишут P(x, y, z).
Оси Ox, Oy, Oz могут образовывать правую или левую систему. Для правой системы поворот от оси Ox к оси Oy на угол, меньший 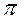 , совершается в направлении против часовой стрелки, если смотреть на плоскость xOy из какой-либо точки положительной полуоси Oz (положительная сторона плоскости xOy). рис.1.6.
, совершается в направлении против часовой стрелки, если смотреть на плоскость xOy из какой-либо точки положительной полуоси Oz (положительная сторона плоскости xOy). рис.1.6.
Правая система Левая система
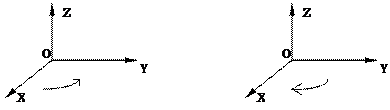
Рис. 1.6
Замечание. Когда мы изучали комплексные числа, то, наряду с декартовой системой координат, рассматривали полярную систему координат на плоскости, которая задается точкой О(полюсом) и полярной осью - лучом, выходящим из полюса. Связь прямоугольных и полярных координат задается формулами:
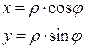 , где
, где 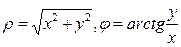 (1.3.1)
(1.3.1)
Дата добавления: 2015-12-10; просмотров: 1487;
