Волновой фронт. Плоские, сферические и цилиндрические волны
Упругие волны в безграничных средах
В данной главе вводится ряд определений и понятий физической акустики, рассматриваются волны в безграничных средах, дается представление о волновом уравнении и его характеристических свойствах.
Волновое уравнение
Многообразие различных волновых процессов в первом приближении описывается волновым уравнением
 , (1.1)
, (1.1)
где 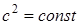 ;
;
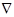 – гамильтониан – инвариантный оператор.
– гамильтониан – инвариантный оператор.
Это линейное гиперболическое уравнение второго порядка. В случае упругих сред, о чем будет сказано ниже, оно описывает малые свободные колебания. Под функцией 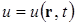 понимаются различные физические величины: давление, смещение, скорость смещения частиц среды и т. д.
понимаются различные физические величины: давление, смещение, скорость смещения частиц среды и т. д.
В случае одного пространственного измерения уравнение (1.1) для плоского случая приобретает наиболее простой вид:
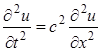 . (1.2)
. (1.2)
Величина с постоянна и имеет размерность скорости. Далее будет ясно, что 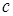 соответствует скорости распространения возмущения. Решением уравнения (1.2) является суперпозиция двух функций:
соответствует скорости распространения возмущения. Решением уравнения (1.2) является суперпозиция двух функций:
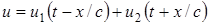 . (1.3)
. (1.3)
Отметим далее важное свойство уравнения (1.2), справедливое и для уравнения (1.1). Величины 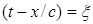 ,
, 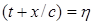 называются характеристиками уравнения (1.2). Будем полагать, что
называются характеристиками уравнения (1.2). Будем полагать, что 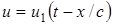 . Находя полную производную по
. Находя полную производную по 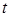 от
от 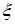 , получим, что
, получим, что 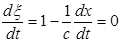 , откуда
, откуда  . Так как
. Так как 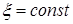 , то возмущение, имеющее в некоторый момент времени
, то возмущение, имеющее в некоторый момент времени 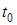 заданную форму
заданную форму 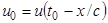 , не изменит ее и в любой другой момент времени. Таким образом, возмущения распространяются, не изменяясь по характеристикам, с постоянной скоростью. Это важное характеристическое свойство уравнения (1.2). В случае трех пространственных переменных говорят уже о характеристических поверхностях.
, не изменит ее и в любой другой момент времени. Таким образом, возмущения распространяются, не изменяясь по характеристикам, с постоянной скоростью. Это важное характеристическое свойство уравнения (1.2). В случае трех пространственных переменных говорят уже о характеристических поверхностях.
В следующем параграфе мы еще вернемся к волновому уравнению (1.2) и его решению (1.3). Здесь же отметим одно обстоятельство, касающееся терминологии. Функцию вида  в определенном контексте называют фазой. Применительно к уравнению (1.2) и решению (1.3) фаза совпадает с характеристикой. В общем случае, это может быть не так, поэтому в следующем параграфе и особенно в параграфе, посвященном явлению дисперсии, понятие фазы не следует отождествлять с характеристиками уравнения (1.2).
в определенном контексте называют фазой. Применительно к уравнению (1.2) и решению (1.3) фаза совпадает с характеристикой. В общем случае, это может быть не так, поэтому в следующем параграфе и особенно в параграфе, посвященном явлению дисперсии, понятие фазы не следует отождествлять с характеристиками уравнения (1.2).
Колебания и волны
Колебания – процессы, при которых состояние системы воспроизводится через определенный промежуток времени. В акустике рассматриваются упругие колебания. Акустические колебания – механические колебания частиц упругой среды. Под упругой средой понимается среда, в которой напряжение есть линейная функция деформации. Колебания можно разделить на две большие группы: свободные и вынужденные. Свободные колебания система совершает, будучи предоставлена самой себе. Реально из-за наличия трения, диссипативных процессов и пр. свободные колебания являются затухающими. Вынужденные колебания система совершает под действием возмущающей силы. Если собственные частоты колебательной системы совпадают с частотой вынуждающих воздействий, то система входит в резонанс.
Упругие колебания в жидкостях и газах характеризуются одной из следующих величин: изменением давления p или плотности r, смещением частиц из положения равновесия u, скоростью колебательного движения v, потенциалом смещения χ или колебательной скорости φ. Следует отличать изменение давления или плотности, связанное с распространением акустических волн, от их статистического (среднего) значения. Все перечисленные величины взаимосвязаны, например: u = grad c; v = grad j; v 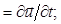
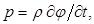 где ρ – плотность среды; t – время.
где ρ – плотность среды; t – время.
Колебания, возникнув в одной точке среды, за счет упругого взаимодействия частиц распространяются с некоторой скоростью c. Волной называют процесс распространения упругого возмущения среды. С математической точки зрения волной имеет смысл называть решение волновых уравнений – главным образом линейных и квазилинейных гиперболических (они имеют одну характерную особенность).
При всем многообразии волновых явлений, линейные волны в одномерном случае могут быть представлены функциями вида
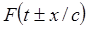 . (1.4)
. (1.4)
Величина 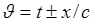 имеет смысл фазы. Отметим здесь, что фаза определена с точностью до аддитивной постоянной. В этой связи уместно сказать, что функция
имеет смысл фазы. Отметим здесь, что фаза определена с точностью до аддитивной постоянной. В этой связи уместно сказать, что функция
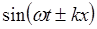 (1.5)
(1.5)
также является решением волнового уравнения (1.2) при определенных соотношениях между 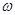 и
и 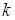 . Для синусоидальных функций фазой будет функция
. Для синусоидальных функций фазой будет функция
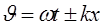 . (1.6)
. (1.6)
Здесь, как и в формулах (1.4), (1.5) знаки «минус» и «плюс» обозначают направление распространения волны: вдоль оси x и в обратном направлении, соответственно.
Волновой фронт. Плоские, сферические и цилиндрические волны
Волновой фронт есть граница между возмущенной и невозмущенной областями упругой среды. Эта граница представляет собой волновую поверхность с нулевой фазой колебаний. Волновой поверхностью называется условная поверхность равной фазы, т. е. это геометрическое место точек, в которых фаза колебаний постоянна. В зависимости от формы волнового фронта выделяют три основных вида волн: плоские, сферические и цилиндрические.
Для плоских волн волновой фронт имеет вид плоскости. Источником таких волн являются плоскопараллельные пластины, испытывающие периодические деформации «растяжения-сжатия» по толщине. В одномерном случае аналитически плоская волна имеет вид (1.4), который легко обобщается на трехмерный случай:
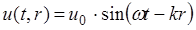 (1.7)
(1.7)
Волновые поверхности сферических волн имеют вид концентрических сфер. Источником сферических волн является точечный объект или сфера малого диаметра. Аналитически сферическая волна – это функции вида
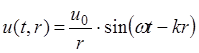 (1.8)
(1.8)
Цилиндрические волны имеют цилиндрический волновой фронт. Их источником является колеблющийся протяженный цилиндр малого диаметра. Уравнения цилиндрических волн – это функции вида
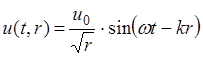 (1.9)
(1.9)
Различия между рассмотренными типами волн не сводятся только к геометрическому различию в форме волновых поверхностей, но имеют и ряд других особенностей. Если пренебречь затуханием, то амплитуда плоской волны не меняется при распространении волны, в то время как амплитуда сферической волны уменьшается с увеличением расстояния 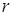 от источника как
от источника как 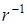 , а цилиндрической – как
, а цилиндрической – как 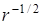 .
.
Не рассматривая подробно понятие интенсивности звуковых волн, укажем, что для плоских волн интенсивность – величина постоянная, для сферических волн интенсивность обратно пропорциональна квадрату расстояния, а для цилиндрических волн интенсивность обратно пропорциональна расстоянию. В табл.1 приведены характеристики перечисленных типов волн в зависимости от формы волнового фронта.
Таблица 1
Основные типы волн
| Волновая поверхность | Аналитическое выражение | Интенсивность |
| Плоская | 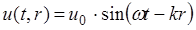
| 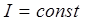
|
| Цилиндрическая | 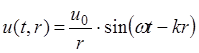
| 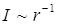
|
| Сферическая | 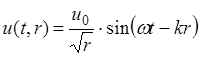
| 
|
Дата добавления: 2015-12-10; просмотров: 9229;
