Волновой вектор плоской монохроматической волны
Плоская монохроматическая волна (ПМВ) для одномерного случая, т.е. при ее распространении вдоль направления оси х, может быть представлена в виде
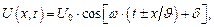
| (1.6) |
где 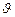 – фазовая скорость ПМВ, определяемая из условия
– фазовая скорость ПМВ, определяемая из условия 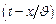 = const;
= const; 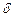 – начальная фаза волны при значении времени
– начальная фаза волны при значении времени 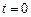 ;
; 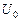 – амплитуда бегущей волны.
– амплитуда бегущей волны.
Термин «плоская» означает, что фронт распространения волны может быть отображен в виде плоскости, а «монохроматическая» – что волна сохраняет при своем движении неизменную частоту ( 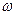 = const) в пространстве и во времени.
= const) в пространстве и во времени.
Если направление распространения ПМВ составляет с осями декартовых координат соответственно углы 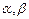 и
и 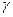 , то выражение (1.6) преобразуется к виду
, то выражение (1.6) преобразуется к виду
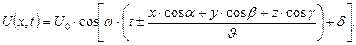
| (1.7) |
Введем в рассмотрение понятие о волновом векторе 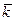 , модуль которого равен
, модуль которого равен 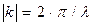 , а его проекции на координатные оси соответственно равны:
, а его проекции на координатные оси соответственно равны:
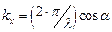 ; ; 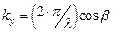 ; ;
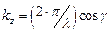 . .
| (1.8) |
Используя понятие скалярного произведения волнового вектора 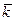 и радиуса вектора
и радиуса вектора 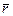 (проекции которого равны: x, y и z), выражение (1.7) приобретает более лаконичный вид:
(проекции которого равны: x, y и z), выражение (1.7) приобретает более лаконичный вид:
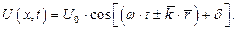
| (1.9) |
Как правило, для облегчения последующих математических операций ПМВ часто представляют в комплексном виде, используя для этого формулу Эйлера:
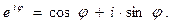
| (1.10) |
В этом случае (на основании формального использования формулы Эйлера) выражение для ПМВ можно представить в комплексной форме:
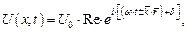
| (1.11) |
где фрагмент (Re) свидетельствует о том, что в выражении (1.11) следует учитывать только действительную часть.
На практике, как правило, фрагмент (Re) не принято обозначать, но по умолчанию его присутствие подразумевается:
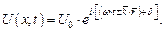
| (1.12) |
Введя в рассмотрение комплексную амплитуду ПМВ ( 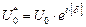 ), выражение (1.12) приобретает более лаконичный вид:
), выражение (1.12) приобретает более лаконичный вид:
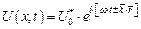 . .
| (1.13) |
Используя представление о волновом векторе ПМВ, выражение (1.3) преобразуется к виду
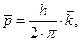
| (1.14) | ||
где 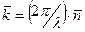 – волновой вектор ПМВ; – волновой вектор ПМВ; 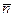 – единичный вектор в направлении распространения фронта ПМВ. – единичный вектор в направлении распространения фронта ПМВ.
| |||
Для случая свободной частицы (т.е. при отсутствии потенциальных полей) полная энергия частицы всецело определяется ее кинетической составляющей 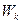 :
:
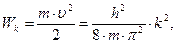
| (1.15) |
где 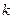 – модуль волнового вектора ПМВ свободной частицы;
– модуль волнового вектора ПМВ свободной частицы; 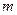 – масса частицы;
– масса частицы; 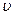 – скорость движения частицы.
– скорость движения частицы.
Поскольку в выражении (1.15) на модуль волнового вектора 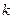 не накладывается никаких ограничений, то полная энергия свободной частицы
не накладывается никаких ограничений, то полная энергия свободной частицы 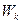 может принимать непрерывный ряд значений в диапазоне величин
может принимать непрерывный ряд значений в диапазоне величин 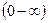 . Именно из этого обстоятельства следует тот факт, что энергия свободной частицы не квантуется.
. Именно из этого обстоятельства следует тот факт, что энергия свободной частицы не квантуется.
Для последующего рассмотрения важно отметить, что ПМВ имеет бесконечную протяженность в пространстве, что, собственно, и следует из фактора ее монохроматичности. Последнее обстоятельство приводит к парадоксальной ситуации, когда речь идет о вероятностных волнах
де Бройля. Согласно разделу (1.1.1.), квадрат модуля амплитуды волны де Бройля в определенной точке пространства является мерой вероятности того, что частица может быть обнаружена в этой точке. В то же время фактор бесконечной протяженности ПМВ в пространстве свидетельствует о том, что квадрат модуля амплитуды волны должен быть тождественно равен нулю. (Правомерность этого утверждения следует из необходимости обеспечения условия нормировки для вероятности нахождения частицы в заданной точке пространства, согласно которому суммарная вероятность нахождения микрочастицы в безграничном пространстве (неважно где) должна быть равна единице.) Следует отметить, что равенство нулю указанных вероятностей для свободной частицы является тривиальным фактом даже с точки зрения здравого смысла, и для установления этого обстоятельства едва ли было бы целесообразным вводить в рассмотрение волны де Бройля. В то же время волны де Бройля могут оказаться небесполезными, если на их основе удастся «сконструировать» вероятностные представления для случая микрочастиц, движение которых происходит в локализованной области пространства (в потенциальном ящике). Эта задача решается ниже в концепции представлений о волновом пакете, образованном из совокупности волн де Бройля.
Дата добавления: 2016-01-03; просмотров: 2058;
