Квантование энергии микрочастицы, находящейся в потенциальном ящике
Как уже отмечалось выше, в квантовой механике движение свободной микрочастицы отображается посредством ПМВ, что свидетельствует об одинаковой вероятности ее нахождения в любой точке физического пространства (и, по сути, эта вероятность тождественно равна нулю – подробнее см. выше).
Движение микрочастицы в потенциальном ящике, с бесконечно высокими стенками, происходит в ограниченной области пространства (частица не имеет возможности выйти за пределы ящика), а следовательно, вероятностное представление ее местонахождения в пространстве будет иметь вид, схематически представленный для случая одномерного движения на рис. 1.2.

Рис. 1.2.Условное отображение функции плотности распределения вероятностей
местонахождения микрочастицы в одномерном потенциальном ящике
Для начального рассмотрения важен не столько сам вид представленной кривой (этот аспект будет рассмотрен позже), а то обстоятельство, что вероятность нахождения микрочастицы непосредственно на границах потенциального ящика должна быть принята равной нулю. Это граничное условие следует из условия непрерывности поведения реальных физических объектов (т.е. при приближении к границе ящика как справа, так и слева должна наблюдаться одинаковая вероятность местонахождения микрочастицы). Отсюда следует, что движению микрочастицы должны соответствовать не любые ПМВ, а лишь те из них, которые могут обеспечить выполнение этого граничного условия.
На рис. 1.3 представлены четыре (из бесконечной совокупности) варианта таких «правильных» ПМВ, суперпозиция которых образует волновой пакет, определяющий вид кривой на рис. 1.3.
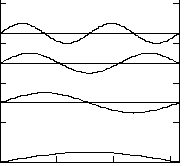
Рис.1.3. Иллюстрация четырех ПМВ (n = 1, 2, 3, 4),
участвующих в образовании волнового пакета
Согласно волновому представлению, изображенному на рис. 1.3, к числу вышеуказанных «правильных» волн следует отнести только лишь те из ПМВ, для которых выполняется условие: 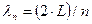 , где параметр n пробегает бесконечный ряд значений из набора величин {1, 2, 3,…, ∞}.
, где параметр n пробегает бесконечный ряд значений из набора величин {1, 2, 3,…, ∞}.
Принимая во внимание результаты раздела 1.1.3, можно заключить, что и модуль волнового вектора волн де Бройля тоже может принимать бесконечный ряд дискретных значений, равных: 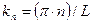 . С учетом выражения (1.15) и вышеизложенных моментов относительно допустимых значений волнового вектора ПМВ можно каждому значению модуля вектора
. С учетом выражения (1.15) и вышеизложенных моментов относительно допустимых значений волнового вектора ПМВ можно каждому значению модуля вектора 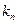 поставить в соответствие вполне определенную волну де Бройля со значением энергии микрочастицы, равным:
поставить в соответствие вполне определенную волну де Бройля со значением энергии микрочастицы, равным:
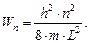
| (1.23) |
Из выражения (1.23) следует фундаментальный вывод о том, что энергия микрочастицы, находящейся в потенциальной яме, может принимать только дискретный ряд значений, т.е. квантуется. Параметр n, характеризующий возможное значение энергии микрочастицы, получил название квантового числа энергетического состояния микрочастицы.
Определим относительное изменение энергии микрочастицы, представленное в виде отношения 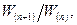 при ее переходе с одного квантового уровня (n) на соседний уровень (n+1). Согласно выражению (1.23) для искомого отношения имеем
при ее переходе с одного квантового уровня (n) на соседний уровень (n+1). Согласно выражению (1.23) для искомого отношения имеем
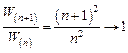 при n→∞. при n→∞.
| (1.24) |
Из выражения (1.24) следует, что наибольшие относительные изменения энергии при квантовых переходах имеют место при малых значениях квантовых чисел n и абсолютно не проявляются на практике при значениях n →∞ . В последнем случае принято считать, что энергетический спектр микрочастицы при больших значениях параметра n имеет непрерывный (а не дискретный) характер.
Можно отметить также то обстоятельство, что в случае выполнения вышеуказанного условия (n ® ¥) количество максимумов (на графиках рис. 1.3) будет крайне велико и располагаться они между собой будут очень плотно. Отсюда можно сделать вывод, что вероятность местоположения микрочастицы будет практически постоянна в любой точке потенциального ящика, как это и принято считать в классической физике, для случая движения шарика по абсолютно ровной и горизонтальной поверхности.
Для последующего рассмотрения необходимо уточнить, что в выражении (1.23) в силу ограничений, накладываемых принципом неопределенности (см. раздел 1.1.4.), речь может идти только о полной энергии микрочастицы. О потенциальной энергии можно говорить только в контексте налагаемого на рассматриваемую систему в целом внешнего (относительно микрочастицы) силового поля, в условиях которого происходит движение микрочастицы. Кинетическая энергия микрочастицы (определяемая, как это общепринято считать в классической физике, в виде разницы полной и потенциальной энергий частицы) в квантовой физике не является параметром, доступным процедуре непосредственного измерения, а следовательно, и не является физическим параметром системы.
В более общей трактовке можно сформулировать фундаментальный вывод о том, что координаты (x, y, z) и проекции импульса (px, py, pz) микрочастицы уже не могут рассматриваться в качестве основных базовых параметров, однозначно характеризующих физическое состояние рассматриваемой системы. Это обстоятельство можно наглядно отобразить с помощью фазового портрета состояния микрочастицы.
На рис. 1.4 представлены фазовые портреты состояния индивидуальной частицы для случаев классического и квантового подходов (на рисунке 6-мерная система координат фазового пространства состояния системы условно представлена как трехмерная). В классическом подходе состояние микрочастицы отображается на фазовом портрете посредством одной единственной точки, с проекциями на оси координат – x, y, z, px, py, pz.
В квантовом подходе следует учесть то обстоятельство, что в соответствии с выражениями (1.21) состояние микрочастицы в фазовом пространстве определяется с некоторой долей неопределенности, величина которой связана с наличием элементарного фазового объема 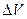 (т.е. это уже не точка):
(т.е. это уже не точка):
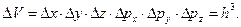
| (1.25) |
На рис. 1.4 положения точки А (классический подход) и объема 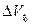 (квантовый подход) характеризуют состояние микрочастицы в фазовом пространстве в начальный момент времени
(квантовый подход) характеризуют состояние микрочастицы в фазовом пространстве в начальный момент времени 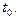 С течением времени микрочастица перемещается в физическом пространстве и в момент времени
С течением времени микрочастица перемещается в физическом пространстве и в момент времени 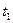 фазовый портрет состояния микрочастицы отображается уже точкой В(классический подход) и объемом
фазовый портрет состояния микрочастицы отображается уже точкой В(классический подход) и объемом 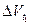 (квантовый подход).
(квантовый подход).

Рис. 1.4. Схематическое отображение фазовых траекторий движения
микрочастицы в классическом и квантовом подходах
Процесс движения микрочастицы при классическом подходе отображается определенной фазовой траекторией (что условно обозначено толстой штрихпунктирной линией), что свидетельствует о жестко детерминированном характере процесса эволюции системы. В случае использования квантового подхода как начальное, так и конечное состояние движущейся микрочастицы содержит элемент неопределенности. В этой связи в последнем случае конечный результат процесса эволюции системы может быть спрогнозирован только на основе вероятностных представлений, представленных выше.
Из вышеизложенного следует, что детерминизм квантовой механики (в части своеобразного проявления причинно-следственных связей в физической системе) имеет своеобразный характер и исключает возможность формирования точного прогноза относительно состояния системы в будущем. Причем эта неопределенность состояния системы испытывает тенденцию к непрерывному возрастанию во времени.
Дата добавления: 2016-01-03; просмотров: 1781;
