Волновая функция как характеристика состояния микрочастицы

Основной задачей разд. 1.1.5 являлось рассмотрение феномена эффекта квантования энергии микрочастицы, локализованной в ограниченной области пространства (т.е. «запертой» в потенциальном ящике). При этом остался открытым вопрос, где именно находится частица в пределах упомянутого потенциального ящика.

Строгое рассмотрение этого вопроса предполагает использование понятия о волновых функциях микрочастицы [1]. Отметим, что волновые представления уже использовались ранее в вышеизложенных материалах в виде элементарных ПМВ де Бройля. Поэтому все нижеизложенные материалы можно рассматривать как дальнейшее развитие волновых представлений квантовой механики.

Волновая функция 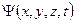состояния микрочастицы формируется таким образом, чтобы квадрат её модуля 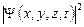представлял собой функцию плотности вероятности распределения микрочастицы 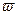. Для случая дискретных возможностей расположения частицы – это просто вероятность обнаружить микрочастицу в момент времени 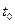в точке пространства с координатами :

,

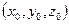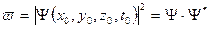(1.26)

где 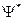– комплексно-сопряженная с 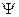волновая функция.

Можно отметить значительную схожесть трактовки физического смысла волновой функции 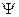и ПМВ де Бройля (см. раздел 1.1.3).

Представляется очевидным, что волновая функция должна удовлетворять условию нормировки:

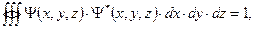
(1.27)

где интегрирование производится по всему геометрическому пространству.

Равенство интеграла (1.27) единице отражает тот очевидный факт, что событие, состоящее в том, что микрочастица будет обнаружена в какой-либо точке геометрического пространства (при этом неважно, в какой именно точке пространства), является достоверным.

Целесообразность введения в рассмотрение функции плотности вероятности 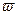обусловлена появившейся возможностью определения вероятности нахождения микрочастицы в ограниченной области пространства (в частности, в пределах потенциального ящика). Действительно, из определения понятия функции плотности вероятности следует, что вероятность нахождения микрочастицы 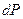в бесконечно малом объеме пространства 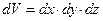равна

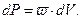
(1.28)

С учетом выражения (1.28), для вероятности нахождения микрочастицы 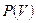в любой области пространства конечного объема 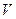имеем (в различных формах представления):

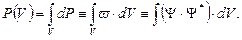
(1.29)

Для полноты рассмотрения вопроса отметим, что набор координат, которые выступают в роли аргументов волновой функции в выражении (1.29), принято называть в квантовой механике полным набором физических величин, характеризующих состояние системы в соответствии со спецификой рассматриваемой задачи. В квантовой механике можно выбрать различные варианты полных наборов величин. Выбранный полный набор величин определяет представление волновой функции. Наибольшее распространение в инженерно-физической практике получило координатное представление ( 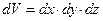) и импульсное представление ( 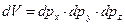). В первом случае определяется местоположение микрочастицы в обычном геометрическом пространстве, а во втором – в виртуальном импульсном пространстве.

Для волновых функций справедлив принцип суперпозиции, который уже был использован (в неявном виде) в разделе 1.1.5 при формировании волнового пакета из ПМВ де Бройля. Физическая суть принципа суперпозиции состоит в том, что если система может находиться в состояниях, описываемых волновыми функциями из набора индивидуальных функций { 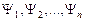}, то она может пребывать и в обобщенном состоянии, описываемом волновой функцией 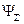, определяемой в виде

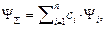
(1.30)

где 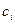– постоянные коэффициенты (в общем случае комплексные), удовлетворяющие условию нормировки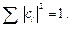

Именно совокупное проявление индивидуальных функций { 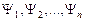} (как результат их суперпозиции в виде волновой функции – 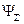) определяет конкретный вид распределения вероятности
нахождения микрочастицы в пределах потенциального ящика (см.
рис. 1.2).

Из наличия у частиц волновых проявлений следует, что закон их движения также должен основываться на волновых принципах. Отсюда следует, что при анализе движения микрочастицы следует руководствоваться неким волновым уравнением. Для микрочастицы, движущейся в силовом поле с потенциальной энергией 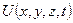, это волновое уравнение имеет следующий вид (уравнение Шредингера, имеющее статус закона природы [2]):

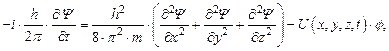
(1.31)

где 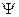– рассмотренная выше волновая функция микрочастицы; 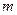– масса микрочастицы; 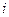– символ мнимой единицы, равный .

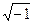Важность волнового уравнения (1.31) состоит в том, что оно отражает процесс эволюции состояний микрочастицы во времени. Следует отметить, что решением уравнения Шредингера являются только комплексные волновые функции. Это обстоятельство не должно вызывать недоразумение, поскольку физическим смыслом обладает только плотность вероятности распределения частиц 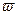(см. выражение (1.26)), а она является действительным числом.

Как правило, аналитическое решение уравнения Шредингера для случая реальных потенциальных функций 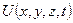связано со значительными математическими трудностями. В этой связи в инженерно-физической практике часто, в целях упрощения анализа, рассматриваются:

· идеализированные модели функции потенциальной энергии 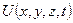, к примеру, рассмотренная выше модель потенциального ящика;

· стационарные задачи (интересные для многих случаев практического применения), в которых функция потенциальной энергии не зависит от времени, т.е. рассматривается функция – .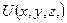

Рассмотрим общие принципы решения волнового уравнения
Шредингера для стационарного случая на примере одномерного (во избежание громоздких выражений) движения микрочастицы. Условие стационарности позволяет представить волновую функцию 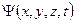в виде произведения независимых координатных и временных функций:

.

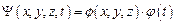(1.32)

Подставив (1.32) в выражение (1.31) и разделив полученное выражение на фрагмент { 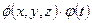}, получим

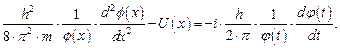
(1.33)

Выражение (1.33) интересно тем, что его левая часть является функцией только координаты местонахождения микрочастицы 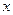, а правая – только времени 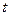. Такая ситуация возможна только в том случае, если обе эти части равны одной и той же постоянной величине. Отметим также, что эта постоянная величина имеет размерность энергии. Можно показать [2], что эта постоянная равна 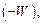где 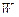– полная энергия микрочастицы (замечания относительно возможности совместного определения потенциальной и кинетической энергии частицы приведены в разделе 1.1.5).

Приравняв правую и левую часть выражения (1.33) 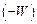и проведя необходимые алгебраические преобразования, получим два уравнения:

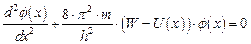	,	(1.34а)
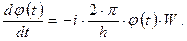
		(1.34б)

Функция 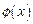, или в общем случае 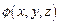, получила название амплитудной волновой функции. Как будет показано ниже (на при­мерах определения энергетических состояний для случая несвобод-
ных частиц), амплитудное уравнение (1.34а) имеет решение только
при строго определенных значениях энергии микрочастицы { 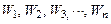}, которые называются собственными значениями энергии частицы. Волновые функции { 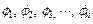}, отвечающие этим значениям энергии, называются собственными волновыми функциями.

Решение уравнения (1.34а) не зависит в явном виде от функции 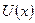и находится посредством интегрирования по методу разделения переменных:

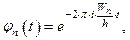
(1.35)

где 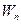– одно из собственных значений энергии микрочастицы.

Из выражения (1.35) следует, что временная зависимость имеет гармонический характер с частотой колебани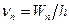й или 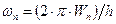(обратить внимание на сходство с выражением (1.2)).

Таким образом, для рассматриваемого стационарного случая полная волновая функция 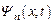для квантового состояния с номером n может быть представлена в виде

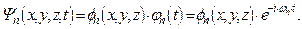
(1.36)

С учетом вышеизложенного вероятность обнаружения микрочастицы 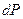в элементе объема 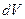будет равна

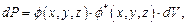
(1.37)

где совокупность координат { 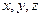} характеризует расположение элементарного объема 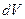в геометрическом пространстве. Эта вероятность 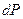для рассмотренного стационарного случая не зависит от времени.