Волновой пакет из вероятностных волн де Бройля
Как отмечалось выше, ПМВ представляет собой бегущую волну, которая имеет бесконечную протяженность в пространстве. В то же время следует отметить, что даже квант света воспринимается как объект, вполне локализованный в ограниченной области пространства. Из этих соображений следует, что отдельный квант света не может быть представлен в виде единственной ПМВ. Ниже будет показано, что создание пространственно-локализованных объектов (микрочастиц или фотонов) возможно путем суперпозиции бесконечного количества индивидуальных ПМВ. Такие пространственно-локализованные объекты, образованные путем суперпозиции большого количества ПМВ, получили название волнового пакета [2].
Создадим прообраз волнового пакета путем суперпозиции бесконечного количества ПМВ, у которых волновой вектор k (в целях упрощения анализа рассматривается одномерный случай согласно выражению (1.6)) пробегает непрерывный ряд значений в интервале значений (k0 – Δk) ÷ (k0 +Δk):
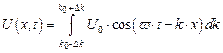 , ,
| (1.16) |
где 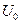 – постоянная величина.
– постоянная величина.
После интегрирования выражения (1.16) и элементарных математических преобразований имеем аналитическое выражение для волнового пакета в виде
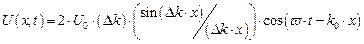 . .
| (1.17) |
Напомним фрагмент выражения (1.17):
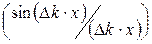 = =
| 
| 1 при условии: ( 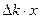 ) → 0 ; ) → 0 ;
| |
| (1.18) | |||
0 при условии: ( 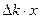 ) = ± ) = ± 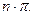
|
В целях наглядности на рис. 1.1 представлены волновые пакеты, построенные для двух случаев: 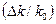 = 0.1 и
= 0.1 и 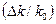 = 0.5. Протяженность центрального фрагмента рисунка 2Δx (при х = 0) условно принимается равной ширине волнового пакета (т.е. области локализации объекта). Из рисунка следует, что увеличение протяженности интервала значений (k0 – Δk) ÷ (k0 +Δk) приводит к повышению степени локализации объекта в пространстве.
= 0.5. Протяженность центрального фрагмента рисунка 2Δx (при х = 0) условно принимается равной ширине волнового пакета (т.е. области локализации объекта). Из рисунка следует, что увеличение протяженности интервала значений (k0 – Δk) ÷ (k0 +Δk) приводит к повышению степени локализации объекта в пространстве.
 а) а) 
|
б) 
|
Рис. 1.1. Зависимость пространственной протяженности волнового пакета 2Δx от относительной величины интервала вариаций Δk : а) – 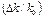 = 0.1; б) – = 0.1; б) – 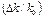 = 0.5 = 0.5
|
С учетом выражения (1.18) (нижнее условие) для определения пространственной протяженности волнового пакета Δx имеем
( 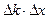 ) = ) = 
| (1.19) |
Из выражения (1.19) следует, что при выполнении условия:
· Δk → ∞, протяженность волнового пакета Δx → 0, т.е. в данном случае имеет место реализация абсолютно локализованного в пространстве объекта (например, идеализированного кванта света);
· Δk → 0, протяженность волнового пакета Δx → ∞, т.е. в данном случае имеет место реализация одной единственной бесконечно протяженной ПМВ с волновым вектором, равным k0(аналог волны де Бройля для свободной частицы);
· Δk = const, протяженность волнового пакета Δx становится равной определенной конечной величине, т.е. в данном случае имеет место реализация цуга волн, отображающего область нахождения реального объекта.
Таким образом, можно считать, что методология формирования волновых пакетов является эффективным способом создания пространственно-локализованных структур (объектов) из бесконечно протяженных составляющих, имеющих волновую природу, вне зависимости от физической специфики рассматриваемых волновых процессов. В силу оговоренной выше универсальности подобного подхода он нашел весьма широкое распространение не только в оптике (электромагнитные волны), но в электронике (спектральный анализ электрических сигналов) и в квантовой механике (вероятностные волны де Бройля). Во всех вышеупомянутых случаях производится «конструирование» локализованных объектов путем суммирования (суперпозиции) большого количества (в пределе бесконечного) индивидуальных ПМВ.
Из выражения (1.14) следует, что интервалу значений Δk соответствует определенный интервал значений Δp (по каждой из координат {x,y,z}):
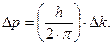
| (1.20) |
Из выражений (1.19) и (1.20) следуют соотношения, известные как принцип неопределенностей В. Гейзенберга:
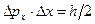 ; ; 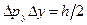 ; ; 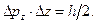
| (1.21) |
Принцип неопределенности свидетельствует о невозможности одновременного и точного определения координат и импульсов микрочастиц (следует особо отметить, что классическая физика не налагает подобного рода принципиальных запретов), а следовательно, становится проблематичным определение потенциальной (фактор 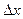 ) и кинетической (фактор Δp) энергии микрочастиц.
) и кинетической (фактор Δp) энергии микрочастиц.
Выражение (1.21) может быть использовано для проведения грубых оценок (с точностью до порядка величины) кинетической энергии микрочастиц, «запертых» в пределах одномерного потенциального ящика, имеющего протяженность 2 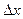 (см. рис. 1.1). Для этой цели, полагая, что Δp ≈ p, можно провести оценку кинетической энергии частицы согласно выражению:
(см. рис. 1.1). Для этой цели, полагая, что Δp ≈ p, можно провести оценку кинетической энергии частицы согласно выражению:
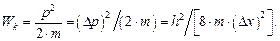
| (1.22) |
В табл. 1.1 представлены зависимости абсолютных Wk и относительных Wk / WT значений кинетической энергии электрона (где WT – средняя энергия теплового движения электрона) от протяженности потенциального ящика (2∙ 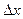 ), полученные на основании выражения (1.22).
), полученные на основании выражения (1.22).
Т а б л и ц а 1.1. Зависимость параметров Wk и Wk / WT от протяженности
потенциального ящика (2 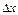 ) (масса покоя электрона: m = 9.11∙10-31кг)
) (масса покоя электрона: m = 9.11∙10-31кг)
2 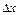 , нм , нм
| 0.2 | 0.5 | 1.0 | 2.0 | 5.0 | 50 | |||||
| Wk, эВ | 5.8 | 1.4 | 0.35 | 5∙10-2 | 1∙10-2 | 3∙10-3 | 6∙10-4 | 1∙10-4 | |||
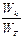
| Т=300 К | 1000 | 60 | 10 | 0.4 | 0.1 | 0.02 | 0.004 | |||
| Т=30 К | 1000 | 600 | 100 | 4.0 | 1.0 | 0.2 | 0.04 | ||||
| Т=3 К | 1∙105 | 2∙104 | 6000 | 1000 | 2.0 | 0.4 |
Примечание: заливкой обозначены ячейки, в которых WT превосходит Wk более чем на порядок.
Данные табл. 1.1 позволяют в некоторой мере оценить влияние на энергетическое состояние микрочастицы масштабного фактора, свидетельствующего об ограничении свободы перемещения микрочастицы в пространстве. В частности из таблицы видно, что при размерах «потенциального ящика» более чем 100 нм влияние фактора ограничения свободы микрочастицы становится пренебрежимо мало относительно возможности проявления физико-химических эффектов, которые могут быть обусловлены проявлением тепловых флуктуаций в системе.
Дата добавления: 2016-01-03; просмотров: 1324;
