Волновая функция свободного электрона. Статистический смысл волновой функции

Уравнение плоской волны имеет вид

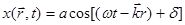(1.13)

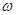где x(r,t) - величина волнообразно распространяющегося возмущения (смещение точки от положения равновесия, напряженность электрического поля и др.); a - амплитуда волны; k - волновой вектор, совпадающий с направлением распространения волны, равный по модулю 2 ; r - радиус-вектор, проведенный в произвольную точку плоскости равной фазы; - круговая частота; t – время; 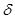- начальная фаза.

Уравнение плоской волны часто представляют в виде комплексной функции

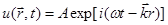, (1.14)

где величина волнообразно распространяющегося возмущения u(r,t) и амплитуда волны А - комплексные величины, причем, .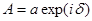

Уравнение (1.14) обладает тем свойством, что его действительная часть совпадает с уравнением (1.13):

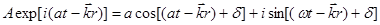, (1.15)

Комплексная амплитуда А объединяет в себе действительную амплитуду а и начальную фазу 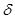. Отметим, что a = | A |.

В соответствии с гипотезой де Бройля, каждой свободной частице соответствует волна с частотой

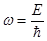
и волновым вектором

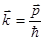
Следовательно, для свободной частицы с не равной нулю массой покоя волновую функцию, которую принято обозначать 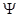(r,t), можно записать в виде:

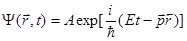(1.16)

Волну, описываемую функцией вида (1.16), соответствующую свободной частице с энергией Е и импульсом p, называют волной де Бройля. Под Е в этих формулах понимают полную энергию частицы, смысл которой раскрывается в теории относительности.

Выясним физическую интерпретацию волновой функции 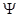(r,t). Очевидно, что с волной вида (1.16) нельзя связать частицу, т.к. частица локализована в пространстве, т.е. обладает вполне определенными значениями координат в определенный момент времени, а волна безгранична в пространстве. На первых этапах развития квантовой физики делались попытки представить частицу как суперпозицию волн. В силу математической теоремы Фурье из плоских волн с различными частотами и волновыми векторами можно составить волновой пакет, имеющий сколь угодно малое протяжение в пространстве. Групповая скорость волн де Бройля

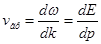(1.17)

совпадает со скоростью частицы v. Эти попытки не привели к успеху, поскольку, как показывает детальный анализ, волновой пакет расплывается с течением времени в пространстве и, следовательно, не может характеризовать стабильную во времени частицу.

Нельзя принять и противоположную точку зрения, согласно которой волны распространяются в среде, состоящей из частиц, подобно, например, звуковым волнам. Такая точка зрения предполагает, что волновые свойства присущи только ансамблю из многих частиц, а не отдельным частицам. Этой точке зрения противоречат опыты, проведенные в 1948 году В.А. Фабрикантом, Л.В. Биберманом и Н.Г. Сушкиным. Они использовали настолько слабый пучок электронов, что интервал времени между пролетом каждого электрона в тысячи раз превышал время пролета электрона. В этом эксперименте исключалось влияние электронов друг на друга. При такой постановке опыта на экране, покрытом флюоресцирующим составом, появлялись отдельные точки - следы попадания электронов. При прохождении через дифракционную решетку большого числа электронов обнаруживалось, что эти точки не распределяются на экране равномерно, а группируются там, где в опытах с интенсивными электронами пучками располагаются дифракционные максимумы. В этих опытах, кроме доказательства того факта, что волновые свойства присущи отдельному электрону, отчетливо проявилось также свойство неделимости микрочастиц.

Анализ опытов по дифракции отдельных электронов показывает, что при точно заданной энергии движущихся электронов нельзя заранее предсказать в какую точку экрана попадет конкретный электрон. Можно лишь утверждать, что существует определенная вероятность попадания его в ту или иную точку экрана. Величина этой вероятности может быть оценена по плотности следов электронов в данном месте экрана после прохождения через прибор многих электронов.

Впервые вероятностное истолкование волновой функции было предложено М. Борном: интенсивность волны де Бройля в каком-либо месте пространства пропорциональна вероятности обнаружить частицу в этом месте. Поскольку интенсивность волны определяется квадратом ее амплитуды (для комплексных величин - квадратом модуля), то для плотности вероятности обнаружения частицы в различных местах пространства можно записать следующее выражение:

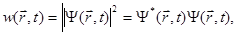(1.18)

здесь

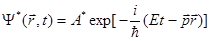(1.19)

комплексно сопряженная функция.

Следует особо отметить, что комплексный характер волновой функции 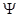(r,t) имеет в квантовой физике принципиальное значение. Все физические величины, имеющие реальный физический смысл, выражаются через всю комплексную функцию 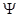(r,t), а не только через ее вещественную часть, как это принято в классической физике.

Используя определение плотности вероятности обнаружения частицы, можно определить вероятность нахождения частицы в любом объеме пространства V. Эта вероятность вычисляется с помощью одного из следующих интегралов:

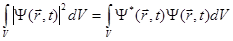(1.20)

Интегрирование производится по всему объему V.