Частица в одномерной прямоугольной потенциальной яме

В этом и последующих разделах будут рассмотрены конкретные примеры решения некоторых наиболее важных квантово-механических задач, описывающих поведение микрочастиц в различных силовых полях. В качестве первого примера рассмотрим одномерную задачу о поведении микрочастицы, находящейся в силовом поле с распределением потенциальной энергии U(x), показанном на рис. 1.2. В этой задаче U(x) = 0 в области 0 < x < L, называемой “потенциальной ямой”, и U(x) = 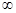вне этой области. Такая простая физическая задача может быть решена аналитически точно и на ее примере можно рассмотреть вопрос о квантовании энергии микрочастицы. С другой стороны, эта физическая модель имеет применение в некоторых реальных задачах ядерной физики и физики твердого тела.

Уравнение Шредингера в одномерном случае для частицы массой m внутри прямоугольной потенциальной ямы запишется в виде

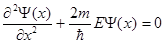(1.29)

Будем искать общее решение уравнения (1.29) в виде

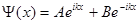(1.30)

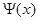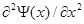где k - некоторый действительный параметр, который будет определен в результате подстановки решения (1.30) в уравнение (1.29). Вычисляя вторую производную волновой функции и подставляя и в уравнение Шредингера (1.29), получим равенство, определяющее волновое число k через полную энергию микрочастицы Е:

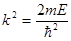(1.31)

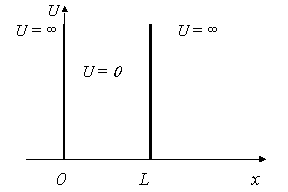
Рис. 1.2. Одномерная прямоугольная потенциальная яма

Следовательно, полная энергия микрочастицы в потенциальной яме определяется ее волновым числом и массой:

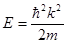(1.32)

Рассмотрим теперь поведение волновой функции на границах потенциальной ямы. В классической физике частица с конечной энергией Е не может попасть в область, где потенциальная энергия бесконечна. В квантовой механике это соответствует требованию обращения в нуль в этой области плотности вероятности w и, следовательно, самой волновой функции 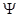. В соответствии с этим требованием для нашей задачи на левой границе потенциальной ямы

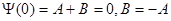
Для правой границы (x=L)

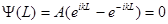
Согласно формуле Эйлера 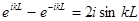, последнее граничное условие будет выполняться при значениях волнового числа

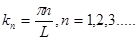(1.33)

Следовательно, и энергия микрочастицы в потенциальной яме может принимать не любые, а строго определенные дискретные или квантованные значения:

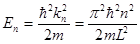(1.34)

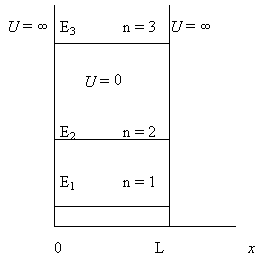
Рис. 1.3. Энергия частицы в прямоугольной потенциальной яме

Энергетический спектр частицы в прямоугольной потенциальной яме схематически показан на рис. 1.3. Целое положительное число n, определяющее значение энергии частицы, называется квантовым числом. Необходимо отметить, что минимальная из возможных значений энергия частицы Е₁ (n = 1) отлична от нуля. Этот результат вытекает также и из принципа неопределенностей Гейзенберга. Действительно, если бы микрочастица находилась в состоянии покоя, то она одновременно обладала бы определенными значениями координаты (x = const) и импульса p = 0, что противоречит соотношениям неопределенностей Гейзенберга.

Значения полной энергии микрочастицы E_n, для которых уравнение Шредингера имеет решения, называются собственными значениями энергии.

Оценим расстояние между соседними уровнями энергии для различных значений массы частицы m и ширины потенциальной ямы L. Разность энергий двух соседних уровней при n >> 1

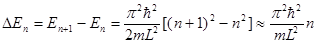
Если масса молекулы порядка ~10^-26 кг, а L порядка 10 см (молекула газа в сосуде), то разность энергий двух соседних стационарных состояний

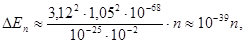
где 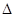E_n – разность энергий, Дж. Столь густо расположенные энергетические уровни молекулы будут восприниматься как сплошной спектр энергии.

Результат практически не изменится, если в качестве частицы взять электрон (m ~ 10^-30 кг), оставив те же размеры потенциальной ямы. Этот случай соответствует свободному электрону в металле, электрону в электронно-лучевой трубке осциллографа и т.д.:

.

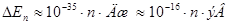Такие разности энергии между соседними уровнями так же, как и в предыдущем примере недоступны для экспериментальных измерений.

Результат получится совсем другой, если область, в пределах которой может находиться электрон, будет порядка размеров атома (~10^-10 м). В этом случае

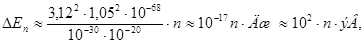
Дискретность энергетических уровней в этом случае весьма заметна.

Волновые функции, являющиеся решениями стационарного уравнения Шредингера для собственных значений энергии E_n называются собственными волновыми функциями. Как было показано выше, для частицы в прямоугольной потенциальной яме собственные волновые функции имеют вид

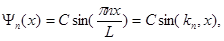
здесь С = 2i A.

Константа С находится из условия нормировки волновой функции. Это условие соответствует очевидному утверждению, что вероятность обнаружить частицу в каком-либо месте потенциальной ямы, т.е. для интервала значений 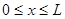, равна 1. Следовательно, условие нормировки в данном случае будет иметь вид

.

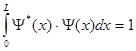Отсюда

.

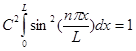Интеграл в этом выражении, как известно, равен L/2, следовательно

.

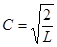Теперь можно в явном виде записать выражения для собственных функций частицы в одномерной прямоугольной потенциальной яме:

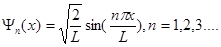(1.35)

На рис. 1.4,а схематически показаны первые три собственные волновые функции для частицы в одномерной прямоугольной потенциальной яме. На рис. 1.4,б приведены соответствующие распределения плотности вероятности положения частицы в потенциальной яме:

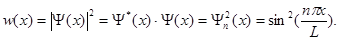
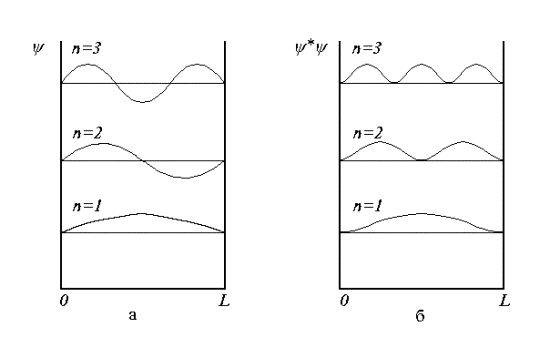
Рис. 1.4. Графики собственных волновых функций: а - плотностей вероятностей; б - для первых трех значений квантового числа