Прохождение частиц через потенциальный барьер. Туннельный эффект
Рассмотрим поведение квантовомеханической частицы при прохождении через потенциальный барьер конечной ширины (рис.1.7). Ограничимся рассмотрением одномерной задачи, когда ось x параллельна движению частицы. В каждой из трех областей I, II и III потенциальная энергия микрочастицы постоянна, но при переходе из одной области в другую меняется скачком. Эта задача моделирует многие физически важные явления, например, выход электронов из металлов, распад атомных ядер и др.
Уравнение Шредингера в этом случае будет иметь вид
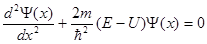 , (1.40)
, (1.40)
где E - полная энергия частицы, а потенциальная энергия

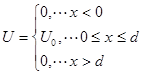 .
.
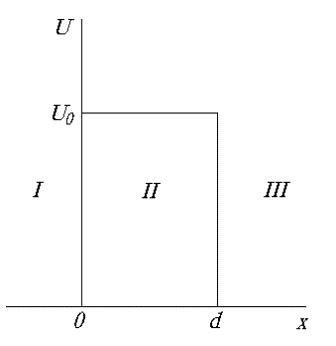
Рис. 1.7. Потенциальный барьер конечной ширины
В области I уравнение (1.40) будет иметь вид
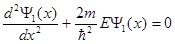 . (1.41)
. (1.41)
Частное решение уравнения (1.41) будем искать в виде волны, распространяющейся вдоль положительного направления оси x:
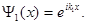 (1.42)
(1.42)
Подставляя (1.42) в (1.41), получим
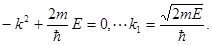 (1.43)
(1.43)
Общее решение уравнения (1.41) для области I представляет собой суперпозицию плоских волн, распространяющихся в противоположных направлениях оси x:
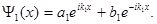 (1.44)
(1.44)
Для области II уравнение Шредингера запишется в виде
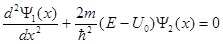 . (1.45)
. (1.45)
Общее решение этого уравнения будет иметь вид
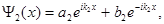 (1.46)
(1.46)
где волновое число в области II
 (1.47)
(1.47)
Уравнение Шредингера для микрочастицы в области III будет иметь тот же вид, что и в области I. Общее решение для этой области будет отличаться от решения (1.44) тем, что в области III нет отраженной волны (b3 = 0)
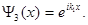 (1.48)
(1.48)
Для вычисления коэффициентов a1, b1, a2, b2 и a3 воспользуемся граничными условиями, согласно которым на границах областей волновая функция и ее первая производная должны быть непрерывны.
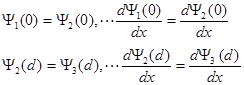 (1.49)
(1.49)
Для простоты вычислений можно положить a1=1, т.к. все коэффициенты b1, a2, b2 и a3 можно, не изменяя общности задачи, разделить на a1. Тогда из условий (1.49) получим систему алгебраических уравнений относительно неизвестных b1, a2, b2 и a3
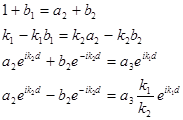 (1.50)
(1.50)
В случае, когда энергия частицы меньше высоты потенциального барьера (E < U), волновое число k2 будет мнимым и его можно представить в виде k2=ik, где
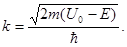 - действительное.
- действительное.
Вероятность обнаружить частицу за потенциальным барьером (в области III) равна квадрату модуля амплитуды, прошедшей в эту область волны: D = |a3|2 = = a3a3* . Величину D называют коэффициентом прозрачности барьера.
Решая систему уравнений (1.50) с учетом граничных условий (1.49), получим следующее выражение для коэффициента прозрачности:
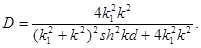 (1.51)
(1.51)
Формулу (1.51) можно значительно упростить, если положить
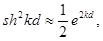
что для реальных ситуаций справедливо, и пренебречь слагаемыми, значительно меньшими, чем экспонента. Тогда
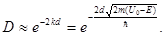 (1.52)
(1.52)
Отсюда видно, что проницаемость барьера сильно зависит от ширины барьера d и величины U0 - E.
В случае потенциального барьера произвольной формы (рис. 1.8) проницаемость барьера выражается приближенной формулой
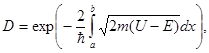 (1.53)
(1.53)
которая, как нетрудно увидеть, является обобщением формулы (1.52).
Таким образом, квантовомеханической частице для преодоления потенциального барьера необязательно иметь энергию больше, чем высота барьера. Она как бы проходит через “туннель” (заштрихованная область на рис. 1.8), расположенном на высоте E, где E - полная энергия микрочастицы. В связи с этим рассмотренное явление называют туннельным эффектом.
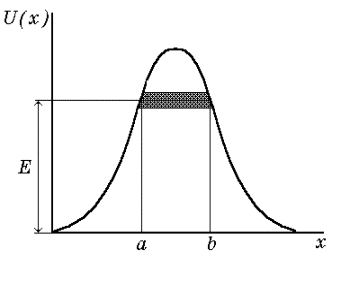
Рис. 1.8. Потенциальный барьер произвольной формы
Дата добавления: 2016-01-09; просмотров: 1455;
