Энергетические зоны в приближении сильной связи

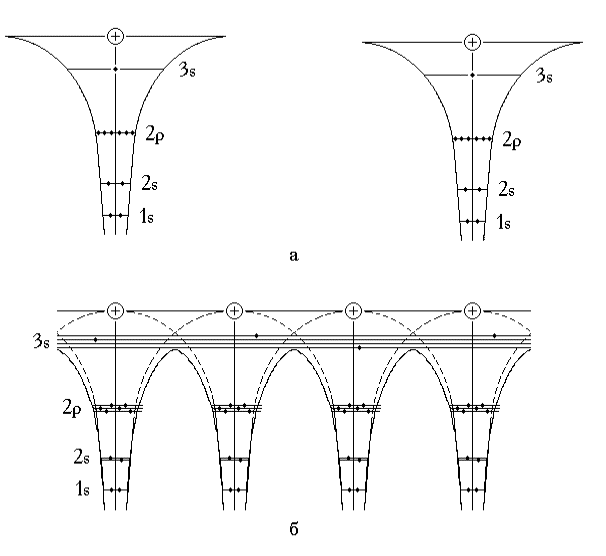
Несмотря на то, что метод сильной связи применим для электронов глубоких энергетических уровней, он хорошо иллюстрирует общие закономерности образования энергетических зон при сближении изолированных атомов и образования из них кристаллической решетки. Рассмотрим качественно картину возникновения энергетических зон на примере образования кристаллической решетки из изолированных атомов натрия. Электронная структура Na¹¹ (1s²2s²2p⁶3s): всего в атоме 11 электронов, по два электрона на 1s и 2s уровнях, 6 электронов на уровне 2р, последний заполненный уровень в атоме натрия - 3s, на котором находится один валентный электрон. Поскольку в приближении сильной связи предполагается, что состояние электрона в кристалле незначительно отличается от его состояния в изолированном атоме, будем в оценке влияния на это состояние кристаллического поля соседних атомов исходить из энергетической структуры изолированного атома. На рис. 2.1,а показаны схематически энергетические уровни и распределение электронов на них для атомов натрия, находящихся на достаточно большом расстоянии друг от друга так, что потенциальные кривые электронов не перекрываются (взаимодействие между атомами пренебрежимо мало). Состояния электронов в этом случае описываются волновыми функциями изолированного атома, разрешенные уровни энергии дискретны и определяются квантовыми числами n, l, m - главным, орбитальным, магнитным соответственно. На каждом невырожденном по энергии уровне могут находиться с учетом спина по два электрона, а на каждом вырожденном по орбитальному квантовому числу уровне 2(2l +1) электронов.

Сблизим теперь эти атомы на расстояние, равное параметру кристаллической решетки натрия (рис. 2.1,б). Взаимодействие с соседними атомами будет оказывать влияние на первоначальные атомные энергетические уровни. В приближении сильной связи предполагается, что потенциальная энергия электрона в кристалле U(r) может быть представлена суммой

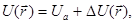(2.2)

где U_a - потенциальная энергия электрона в изолированном атоме; U(r) - поправка, учитывающая влияние соседних атомов. Предполагается, что соседние атомы оказывают слабое возмущение на U_a( U(r) << U_a). Пренебрежение поправкой U(r) приводит к уравнению Шредингера для изолированного атома.

Поскольку в кристалле каждый уровень изолированного атома повторяется N раз, то он становится N-кратно вырожденным. Известно, что электрическое поле снимает вырождение и каждый уровень изолированного атома расщепляется на N близко расположенных (по значениям энергии) энергетических уровней. Здесь имеется аналогия со связанными осцилляторами. Если мы имеем два не связанных между собой каким-либо взаимодействием совершенно одинаковых осциллятора (математические маятники, электрические колебательные контуры и др.), то частоты их собственных колебаний совпадают. Взаимодействие между осцилляторами приводит к расщеплению одной частоты на две близкие частоты (при условии, что энергия взаимодействия между осцилляторами много меньше энергии собственных колебаний). Для N связанных между собой осцилляторов получим полосу из N близко расположенных частот. Аналогичный результат получается для системы взаимодействующих атомов. Число энергетических уровней, на которые расщепляется каждый энергетический уровень изолированного атома, равно числу атомов в кристалле. Величина расщепления тем больше, чем сильнее взаимодействие между атомами, т.е. чем меньше расстояние между ними. На рис. 2.2 показано схематически расщепление двух энергетических уровней атома под воздействием полей соседних атомов. Схема приведена для восьми атомов.

Решение уравнения Шредингера в приближении сильной связи приводит к следующему выражению для энергии электрона в периодическом поле трехмерной кубической решетки

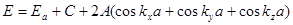, (2.3)

здесь C - некоторая постоянная величина, которая может принимать положительные и отрицательные значения; А - обменный интеграл, зависящий от перекрытия волновых функций атомов; k_x, k_y, k_z - компоненты волнового вектора электрона; а - параметр решетки кристалла.

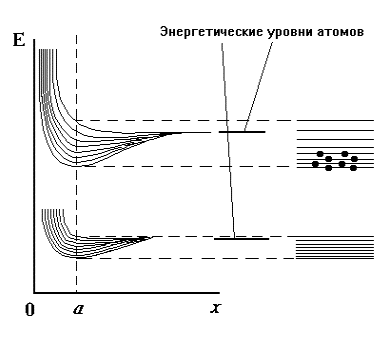
Рис.2.2. Расщепление энергетических уровней атома

Экстремальные значения энергии электрона Е имеют место при cosk_ia = ± 1 (i = x, y, z) и определяют ширину энергетической зоны, образованной расщепленным уровнем изолированного атома. Для простой кубической решетки ширина энергетической зоны E= 12A. Ширина энергетической зоны для более высоких уровней больше, т.к. для этих состояний электронов сильнее перекрываются волновые функции электронов и, следовательно, больше обменный интеграл А. Середина зоны сдвинута относительно положения энергетического уровня изолированного атома на величину С. Направление смещения зависит от знака С. Энергетические зоны в общем случае разделены интервалами энергии E_g, называемыми запрещенными зонами. Иногда энергетические зоны могут перекрываться.

В реальных кристаллах размером приблизительно 1 см³ содержится ~ 10²² атомов. Ширина энергетической зоны обычно ~ 1 эВ. В этом случае расстояние между уровнями в зоне составляет ~ 10^-22 эВ. Следовательно, спектр электронов в пределах энергетической зоны можно считать практически непрерывным.