Водородоподобные атомы
Атомы, содержащие один внешний электрон называются водородоподобными. Потенциальная энергия электрона в таких атомах определяется сферически симметричным полем взаимодействия его с ядром (рис. 1.9):
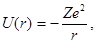 (1.54)
(1.54)
где Z - зарядовое число атома, r - расстояние электрона от ядра.
Для электрона, связанного с атомом, E < 0, а для свободно движущегося вне атома соответствует положительная полная энергия (E > 0).
Уравнение Шредингера для электрона в атоме имеет вид
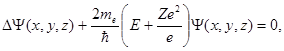 (1.55)
(1.55)
где me- масса электрона.
В сферической системе координат уравнение (1.55) преобразуется к виду
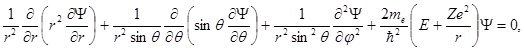 (1.56)
(1.56)
где 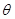 и
и 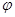 - полярный и азимутальный углы соответственно.
- полярный и азимутальный углы соответственно.
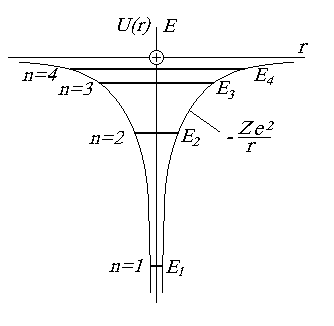
Рис. 1.9. Энергетическая диаграмма водородоподобного атома
Для E < 0 уравнение (1.56) имеет конечные и непрерывные решения только для дискретных значений энергии
 , (1.57)
, (1.57)
Собственные функции, удовлетворяющие уравнению (1.56), зависят от трех целочисленных параметров n, l и m:
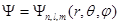
Параметр n называется главным квантовым числом и определяет полную энергию электрона в атоме (см. формулу (1.57)). Этим числом обозначают номер энергетического уровня электрона в атоме (рис. 1.9).
Параметр l определяет модуль момента импульса электрона в атоме:
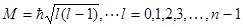
и называется азимутальным или орбитальным квантовым числом. При данном главном квантовом числе n квантовое число l может принимать n различных значений от 0 до n-1.
Параметр m определяет величину проекции момента импульса на некоторое направление z
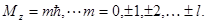
Этот параметр называется магнитным квантовым числом.
Таким образом, каждому значению энергии электрона в атоме соответствует несколько состояний, отличающихся квантовыми числами l и m, и собственными волновыми функциями 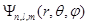 . Такие состояния называются вырожденными. Кратность вырождения, т.е. число различных состояний с данным значением энергии, как нетрудно убедиться, будет равно
. Такие состояния называются вырожденными. Кратность вырождения, т.е. число различных состояний с данным значением энергии, как нетрудно убедиться, будет равно 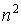 .
.
Волновая функция 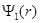 состояния с наинизшей энергией (n = 1) в сферически симметричном случае имеет вид
состояния с наинизшей энергией (n = 1) в сферически симметричном случае имеет вид
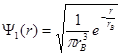 , (1.58)
, (1.58)
где 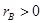 . Физический смысл этого параметра будет понятен из дальнейшего анализа.
. Физический смысл этого параметра будет понятен из дальнейшего анализа.
Функция 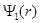 определяет, как обычно, объемную плотность вероятности обнаружения электрона в пространстве. Более наглядное представление можно получить с помощью радиальной плотности вероятности
определяет, как обычно, объемную плотность вероятности обнаружения электрона в пространстве. Более наглядное представление можно получить с помощью радиальной плотности вероятности 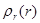 . Эта величина вводится таким образом, чтобы произведение
. Эта величина вводится таким образом, чтобы произведение 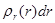 определяло вероятность обнаружения электрона на расстоянии от ядра между r и r+dr. Расчеты приводят к следующему выражению для
определяло вероятность обнаружения электрона на расстоянии от ядра между r и r+dr. Расчеты приводят к следующему выражению для 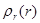 :
:
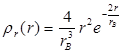 .
.
На рис. 1.10 представлен график функции 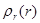 . Он имеет максимум при r=rB. Для атома водорода численное значение rB совпадает с радиусом первой боровской орбиты. Следовательно, в квантовой физике радиус первой боровской орбиты соответствует такому расстоянию от ядра, на котором вероятность обнаружения электрона максимальна.
. Он имеет максимум при r=rB. Для атома водорода численное значение rB совпадает с радиусом первой боровской орбиты. Следовательно, в квантовой физике радиус первой боровской орбиты соответствует такому расстоянию от ядра, на котором вероятность обнаружения электрона максимальна.
Для полного описания состояния электрона в атоме необходимо к трем квантовым числам n, l, m добавить еще одно - спиновое квантовое число (спин) S. Это квантовое число определяет ориентацию собственного момента количества движения электрона на некоторое направление, например, на направление орбитального момента электрона. Квантовое число S может принимать только два значения: 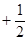 и
и 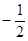 . Наличие спина приводит к удвоению состояний электрона в атоме. Спин не имеет классического аналога, это такое же внутреннее свойство электрона, как его заряд и масса.
. Наличие спина приводит к удвоению состояний электрона в атоме. Спин не имеет классического аналога, это такое же внутреннее свойство электрона, как его заряд и масса.
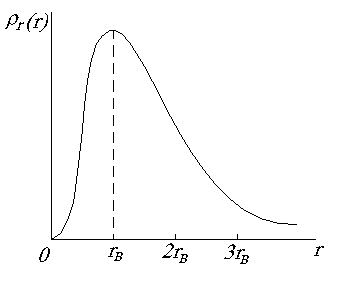
Рис. 1.10. График функции 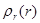 для состояния электрона в атоме водорода с n = 1
для состояния электрона в атоме водорода с n = 1
ГЛАВА 2
Дата добавления: 2016-01-09; просмотров: 1104;
