Уравнение Шредингера. Волновая функция в виде плоской монохроматической волны описывает частный случай движения квантово-механической частицы - движение свободной частицы

Волновая функция в виде плоской монохроматической волны описывает частный случай движения квантово-механической частицы - движение свободной частицы. Именно микрочастица, которая не подвергается какому-либо внешнему воздействию, описывается волной де Бройля. Возникает вопрос, какой вид будет иметь волновая функция и как ее найти, если частица не является свободной, находится, например, во внешнем поле? В классической физике существует уравнение, описывающее движение тела в самом общем случае - это основное уравнение динамики, второй закон Ньютона. В квантовой физике также существует уравнение, с помощью которого можно описать состояние микрочастицы в разнообразных условиях. Это уравнение называется уравнением Шредингера. Так же, как и уравнение Ньютона, уравнение Шредингера не выводится, его справедливость подтверждается многочисленными экспериментальными фактами, являющимися следствием этого уравнения.

Уравнение Шредингера - это дифференциальное уравнение, неизвестной в котором является волновая функция микрочастицы 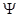(r,t), зависящая в общем случае от координат и времени. В случае потенциальных силовых полей, описываемых потенциальной энергией U(r), общее уравнение Шредингера имеет вид

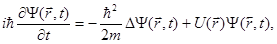(1.23)

здесь i - мнимая единица; m - масса частицы; r - радиус-вектор, определяющий ее положение; 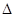- оператор Лапласа, который в прямоугольной декартовой системе координат записывается в виде

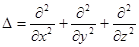(1.24)

Волновая функция - комплексная величина и поэтому физического смысла не имеет. Но нахождение волновой функции в результате решения уравнения Шредингера позволяет вычислить наблюдаемую физическую величину - плотность вероятности или плотность распределения координат частицы w(r,t):

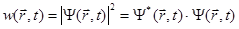(1.25)

Вероятность обнаружения частицы в бесконечно малом элементе объема dV будет равна, очевидно, 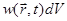, а вероятность обнаружить частицу внутри конечного объема V можно вычислить с помощью интеграла по этому объему: .

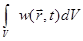Таким образом, задача квантовой механики состоит в определении вероятностей тех или иных событий с помощью волновой функции, являющейся решением уравнения Шредингера. По вероятностям можно найти средние значения случайных физических величин, т.е. рассчитать те параметры, которые можно измерить.

Как любое линейное дифференциальное уравнение в частных производных уравнение Шредингера имеет множество решений. Причем, всякая линейная комбинация любых частных решений также является решением этого уравнения.

Среди решений уравнения Шредингера есть стационарные. Стационарными называются состояния, в которых ни одна из квантово-механических вероятностей не изменяется со временем. Для любого стационарного состояния волновую функцию можно записать в виде

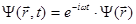(1.26)

где функция 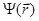зависит только от координат частицы; 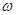- вещественный параметр (частота волновой функции), который связан с энергией этого состояния E равенством .

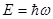С учетом (1.26) уравнение Шредингера принимает вид

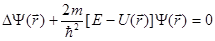(1.27)

Уравнение (1.27) называется уравнением Шредингера для стационарных состояний или стационарным уравнением Шредингера. Волновая функция 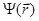, входящая в это уравнение, описывает состояние микрочастицы в стационарных состояниях. Уравнение Шредингера (1.23) называется общим уравнением Шредингера.

Потенциальная функция в уравнениях (1.23) и (1.27) определяется так же, как в классической физике, т.е. как потенциальная энергия точечной частицы, локализованной в некоторой точке силового поля, координаты которой определяются радиусом-вектором r.

Стационарное уравнение Шредингера необходимо дополнить граничными условиями, которые накладывают определенные условия на волновую функцию 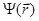на границах областей с разными значениями потенциальной энергии U(r). Физический смысл этих условий заключается в том, что решения уравнения Шредингера должны переходить друг в друга без скачков на границах соседних областей. Для этого необходимо, чтобы на границе раздела областей были однозначны и непрерывны волновая функция и ее первые пространственные производные:

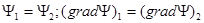(1.28)

где индексы 1 и 2 соответствуют значениям функций на границе двух соседних областей.