Движение микрочастицы в прямоугольной потенциальной яме. Потенциальный барьер в классической механике.
Потенциальный барьер в классической механике.
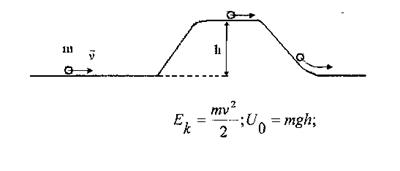
Если  – прохождение.
– прохождение.
Если 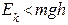 – отражение.
– отражение.
Совсем иначе выглядит поведение частицы согласно квантовой механике:
а) даже при 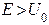 имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону.
имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону.
б) если 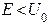 имеется отличная от нуля вероятность того, что частица проникает сквозь барьер и окажется в области, где
имеется отличная от нуля вероятность того, что частица проникает сквозь барьер и окажется в области, где 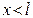 .
.
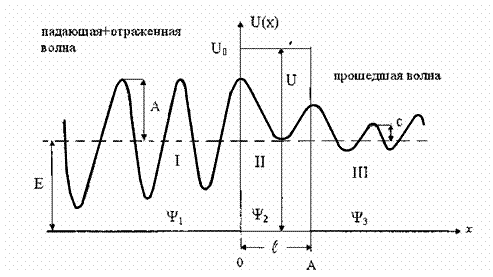
Такое поведение микрочастицы вытекает непосредственно из уравнения Шредингера.
Пусть барьер представляет собой тонкую потенциальную стенку. частица падает на барьер слева.
Область 1: 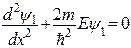 (19)
(19)
Область 2: 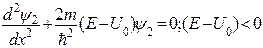 (20)
(20)
Область 3: 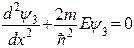 (21)
(21)
Обозначения: 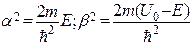 (22)
(22)
Решениями этих уравнений будут функции:
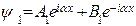 (23)
(23)
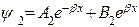 (24)
(24)
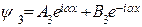 (25)
(25)
 - амплитуда волны, падающей на барьер слева,
- амплитуда волны, падающей на барьер слева,
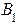 - амплитуда отраженной волны в области I.
- амплитуда отраженной волны в области I.
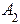 - амплитуда волны, прошедшей через барьер в область II,
- амплитуда волны, прошедшей через барьер в область II,
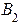 - амплитуда отраженной волны (от поверхности в точке
- амплитуда отраженной волны (от поверхности в точке  ) в области II.
) в области II.
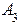 - амплитуда волны, прошедшей в область III,
- амплитуда волны, прошедшей в область III,
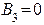 – т.к. в области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо.
– т.к. в области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо.
Решение вида  соответствует волне, распространяющейся в положительном направлении оси
соответствует волне, распространяющейся в положительном направлении оси 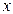 , а решение
, а решение 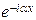 волне, распространяющейся в противоположном направлении.
волне, распространяющейся в противоположном направлении.
Для нахождения остальных коэффициентов воспользуемся условиями, которым должна удовлетворять функция 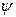 .
.
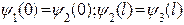 – условие непрерывности (26)
– условие непрерывности (26)
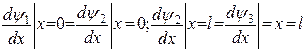 (27)
(27)
Эти условия требуют, чтобы 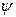 была гладкой, т.е. не имела изломов. Условий (7) и (8) вполне достаточно, чтобы найти различные амплитуды в явном виде. Поскольку плотность вероятности, связанная с волновой функцией, пропорциональна квадрату амплитуды этой функции, мы можем ввести следующие понятия.
была гладкой, т.е. не имела изломов. Условий (7) и (8) вполне достаточно, чтобы найти различные амплитуды в явном виде. Поскольку плотность вероятности, связанная с волновой функцией, пропорциональна квадрату амплитуды этой функции, мы можем ввести следующие понятия.
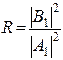 – коэффициент отражения частицы от поверхности барьера в точке
– коэффициент отражения частицы от поверхности барьера в точке 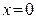 . Он определяет вероятность отражения частицы от потенциального барьера.
. Он определяет вероятность отражения частицы от потенциального барьера.
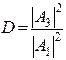 – коэффициент прохождения (или прозрачности).
– коэффициент прохождения (или прозрачности).
В результате вычислений коэффициента прозрачности получаем
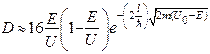 (28)
(28)
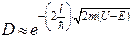 (29)
(29)
Прошедшая волна экспоненциально затухает в пределах барьера.
Вывод: вероятность прохождения частицы через потенциальный барьер сильно зависит:
а) от ширины барьера  ;
;
б) от высоты барьера, точнее от  ;
;
в) от массы частицы m.
Например, если при какой-то ширине барьера  величина
величина 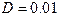 , то при увеличении ширины в 2 раза коэффициент прозрачности уменьшается в 100 раз.
, то при увеличении ширины в 2 раза коэффициент прозрачности уменьшается в 100 раз.
В случае потенциального барьера произвольной формы (29) принимает более общий вид:
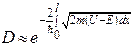 (30)
(30)
где 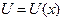 .
.

Парадокс- частица в туннеле должна бы обладать отрицательной кинетической энергией (в туннеле 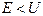 ).
).
При преодолении потенциального барьера частица как бы проходит через туннель в это барьере. В связи с этим рассмотренное явление называют туннельным эффектом. Оно объясняется тем, что микрочастицы обладают волновыми свойствами.
Дата добавления: 2015-12-16; просмотров: 979;
