Движение микрочастицы в прямоугольной потенциальной яме.

Состояние нуклонов в атомном ядре, электронов в атоме, атомов в молекуле, электронов в кристаллической решетке может быть описано как движение обладающих волновыми свойствами микрочастиц в различных потенциальных ямах. Отражение частиц от потенциальных стенок на границах ям обуславливает стабильность атомов, молекул, твердых тел. С возможностью туннелирования частиц сквозь потенциальные барьеры связано явление радиоактивного распада некоторых типов ядер, ковалентная связь между атомами в молекулах, металлическая связь в кристаллах, различные контактные и кинетические явления в твердых телах, помещенных в электрическое поле, автоионизация атомов и холодная эмиссия электронов из металлов и полупроводников. Все эти явления могут быть объяснены только с помощью квантовой механики, т.е. на основе решения уравнения Шредингера для потенциальных ям различной природы, конфигурации, ширины и глубины.

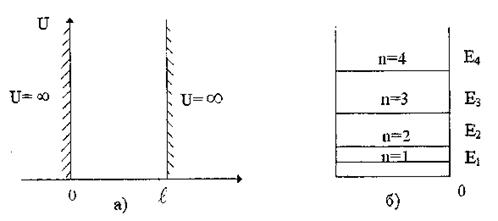
Рис. 3

Найдем собственные значения энергии и соответствующие им собственные значения функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

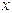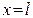Предположим, что частица может двигаться только вдоль оси . Пусть движение ограничено непроницаемыми для частицы стенками: и . Потенциальная энергия 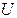имеет в этом случае вид:

(4)

Уравнение Шредингера (3) для данного случая:

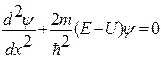(5)

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и функция 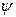за пределами ямы равна нулю. Из условия непрерывности следует, что 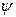должна быть равна нулю на границах ямы, т.е. что

(6)

Внутри потенциальной ямы уравнение (5) имеет вид

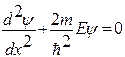(7)

Введя обозначение

(8)

придем к уравнению, хорошо известному из теории колебаний

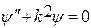(9)

Решение этого уравнения имеет вид

(10)

Постоянные 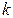и 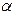должны удовлетворять граничным условиям (6)

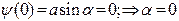(11)

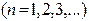(12)

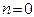отпадает, поскольку при этом получается , что означает, что частица нигде не находится.

Подставив значение 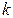из (12) в равенство (8), получив собственные значения энергии частицы

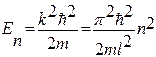
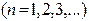(13)

Энергия электрона принимает дискретные значения 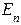. На рис. 3б изображена схема энергетических уровней. Это резко противоречит классическим представлениям, согласно которым энергия изменяется непрерывно.

Из (13) следует, что 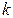имеет смысл волнового вектора соответствующих волн де-Бройля для электрона. Действительно, по формуле де-Бройля

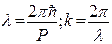– волновое число (14)

Тогда подставляя (14) в (13), получаем для энергий электрона выражение в естественном «классическом» виде

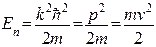(15)

Квантование энергии происходит потому, что волновое число 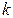,а значит и импульс квантуется согласно (12). Подставив значения 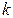из (12) в (10), получим собственные волновые функции задачи

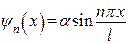(16)

Для нахождения коэффициента 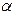воспользуемся условием нормировки, которое в данном случае запишется следующим образом

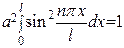(17)

откуда . Таким образом, собственные волновые функции имеют вид

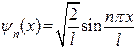
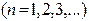(18)

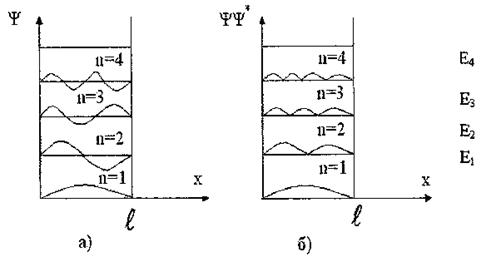
Рис. 4

Графики волновых функций изображены на рис. 4а. На рисунке 4б дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная 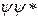. Из графиков, например, следует, что в состоянии 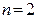частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и вправой половине ямы. Такое поведение частицы, очевидно, несовместно с представлением о траекториях. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.