Примеры квантования энергии микрочастиц в физических системах
а) Идеализация потенциальных атомных диаграмм
В настоящем разделе приведены примеры решения уравнения Шредингера для ряда конкретных физических систем, широко используемых в современной инженерно-физической практике. Ограниченный объем пособия не предполагает проведения детального рассмотрения данных материалов. В этой связи основной целью раздела является
изучение основных методологических принципов анализа квантовых стационарных систем на примерах движения микрочастиц в условиях [8]:
· отсутствия потенциальных полей как таковых (специальный случай, адекватный вероятностным волнам де Бройля);
· нахождения в потенциальном ящике конечной протяженности с бесконечно высокими стенками;
· электростатического механизма взаимодействия микрочастиц (электрона с протоном в водородоподобном атоме);
Как отмечалось выше, практическое использование уравнения Шредингера сопряжено со значительными математическими трудностями. Эффективность процесса минимизации указанных математических трудностей напрямую связана с решением вопроса «оптимизации» используемых потенциальных функций 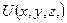 . Под оптимизацией принято понимать процедуру замены реальных потенциальных функций взаимодействия микрочастиц на их упрощенные (идеализированные) модели, которые, тем не менее, адекватны целям рассматриваемой задачи.
. Под оптимизацией принято понимать процедуру замены реальных потенциальных функций взаимодействия микрочастиц на их упрощенные (идеализированные) модели, которые, тем не менее, адекватны целям рассматриваемой задачи.
В инженерно-физической практике анализа микроскопических (атомно-молекулярных) и макроскопических систем (конденсированные среды) в качестве базовой потенциальной функции 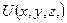 часто используется выражение вида [3]
часто используется выражение вида [3]
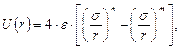
| (1.38) |
где r –межцентровое расстояние микрочастиц; n и m – постоянные величины, численное значение которых определяется типом механизма взаимодействия микрочастиц (выполняется условие: n > m); 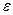 и
и 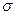 – постоянные, определяемые экспериментальным путем для каждого типа взаимодействующих микрочастиц (в частности, для случая атомно-молекулярных взаимодействий (потенциал Леннарда-Джонса [3]):
– постоянные, определяемые экспериментальным путем для каждого типа взаимодействующих микрочастиц (в частности, для случая атомно-молекулярных взаимодействий (потенциал Леннарда-Джонса [3]):
n = 12; m = 6).
Первое слагаемое в выражении (1.38) характеризует проявление сил взаимного отталкивания между микрочастицами, второе – сил взаимного притяжения. На рис. 1.5 представлены примеры графического отображения процедуры проведения идеализации (варианты (Б) и (В)) потенциальной функции 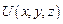 вида (1.38).
вида (1.38).


Рис. 1.5. Варианты представления потенциальной функции 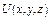
(А – реальная функция, по (1.38); Б – идеализация № 1;
В – идеализация № 2)
Из материалов рис.1.5 следует, что на некоторых участках оси r функция 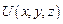 принимает отрицательные значения. Последнее обстоятельство является следствием наложенного требования о равенстве
принимает отрицательные значения. Последнее обстоятельство является следствием наложенного требования о равенстве 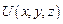 = 0 при r → ∞. Факт появления отрицательных значений энергии не должен вызывать особого недоразумения, поскольку в расчетной практике представляют интерес не абсолютные значения энергий (уровни квантования энергии), а их разностные формы, определяющие энергетические параметры конкретных элементарных физико-химических процессов.
= 0 при r → ∞. Факт появления отрицательных значений энергии не должен вызывать особого недоразумения, поскольку в расчетной практике представляют интерес не абсолютные значения энергий (уровни квантования энергии), а их разностные формы, определяющие энергетические параметры конкретных элементарных физико-химических процессов.
б) Движение микрочастицы в условиях отсутствия
потенциальных полей
В отсутствие потенциального поля (т.е. при условии: 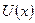 = 0) движение микрочастицы следует рассматривать как абсолютно свободное и стационарное. Уравнение Шредингера для этого типа движения микрочастицы в одномерном приближении имеет вид
= 0) движение микрочастицы следует рассматривать как абсолютно свободное и стационарное. Уравнение Шредингера для этого типа движения микрочастицы в одномерном приближении имеет вид
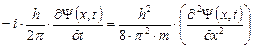 . .
| (1.39) |
С учетом стационарного характера движения микрочастицы решением этого уравнения является полная волновая функция (см. выражение (1.36)):
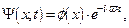
| (1.40) |
где 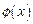 – амплитудная волновая функция, удовлетворяющая амплитудному уравнению (1.34).
– амплитудная волновая функция, удовлетворяющая амплитудному уравнению (1.34).
При выполнении условия 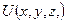 = 0 для амплитудного волнового уравнения
= 0 для амплитудного волнового уравнения 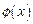 имеем
имеем
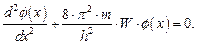
| (1.41) |
Поскольку в данном случае полная энергия микрочастицы равна ее кинетической энергии, то с учетом выражения (1.15) для амплитудного уравнения имеем
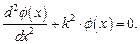
| (1.42) |
Частными решениями амплитудного уравнения (1.42) являются:
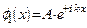 и и 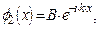
| (1.43) |
где параметры, стоящие перед экспонентами, А и В – постоянные коэффициенты.
С учетом выражения (1.40), решая уравнение (1.39), для полной волновой функции 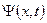 имеем
имеем
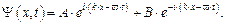
| (1.44) |
Уравнение (1.44) отражает суперпозицию двух ПМВ де Бройля (как это и следовало ожидать, согласно материалам раздела 1.1.2), распространяющихся в противоположных направлениях вдоль оси x геометрического пространства.
Для последующего изложения необходимо отметить, что энергия движения свободной микрочастицы (то есть при выполнении условия: 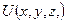 = 0) не квантуется (поскольку нет никаких ограничений на допустимые значения модуля волнового вектора – k), ее изменение может иметь непрерывный характер, а ее величина пропорциональна квадрату модуля волнового вектора (подробнее см. выражение (1.15)).
= 0) не квантуется (поскольку нет никаких ограничений на допустимые значения модуля волнового вектора – k), ее изменение может иметь непрерывный характер, а ее величина пропорциональна квадрату модуля волнового вектора (подробнее см. выражение (1.15)).
в) Квантование энергии микрочастицы, находящейся
в потенциальном ящике
Определим энергетический спектр микрочастицы при ее движении в пределах потенциального ящика (используется модельное представление согласно рис. 1.5,В). Для этого рассмотрим случай движения микрочастицы в условиях внешнего силового поля, определяемого потенциальной функцией 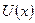 вида
вида
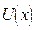 = =
| 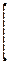
| U0, при x < 0 – (область № I); | |
0, при 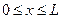 – (область № II); – (область № II);
| (1.45) | ||
| U0, при x > 0 – (область № III). |
Уравнения Шредингера (см. (1.34а)) для вышеуказанных областей оси x имеют соответственно вид
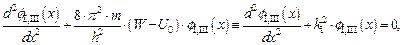
| (1.46) |
где 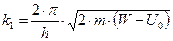 ;
;
 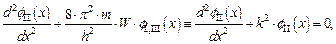
| (1.47) |
где 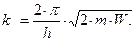
Для упрощения рассмотрения задачи положим, что стенки потенциального ящика являются бесконечно высокими, а следовательно, решение уравнения (1.46) имеет вид
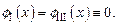
| (1.48) |
Общим решением уравнения (1.47), характерного для случая нахождения микрочастицы в пределах потенциального ящика, является:
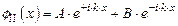 . .
| (1.49) |
Воспользовавшись условием непрерывности волновой функции 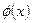 на левой границе
на левой границе 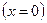 потенциального ящика, имеем
потенциального ящика, имеем
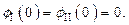
| (1.50) |
Из выражения (1.50) следует, что постоянные коэффициенты A и B, используемые в выражении (1.49), удовлетворяют условию: 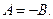 С учетом этого обстоятельства для волновой функции
С учетом этого обстоятельства для волновой функции 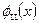 находим:
находим:
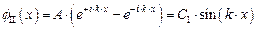 . .
| (1.51) |
Воспользовавшись условием непрерывности волновой функции 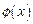 на правой границе
на правой границе 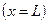 потенциального ящика, имеем
потенциального ящика, имеем
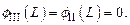
| (1.52) |
Из выражений (1.51) и (1.52) следует весьма существенное следствие:
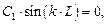
| (1.53) |
что представляется возможным (если 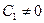 ) только лишь в том случае, если выполняется условие:
) только лишь в том случае, если выполняется условие: 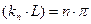 , где n = 1, 2, 3,…, ∞.
, где n = 1, 2, 3,…, ∞.
С учетом этого условия для амплитудной волновой функции имеем
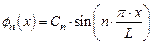 , ,
| (1.54) |
где значения постоянных коэффициентов Cn определяются из условия нормировки амплитудной волновой функции.
Искомое энергетическое состояние микрочастицы, описываемое волновой функцией (1.54), можно получить, подставив дискретные величины kn в выражение (1.15):
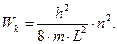
| (1.55) |
Из выражения (1.55) следует, что при больших значениях L, намного превосходящих атомные масштабы, расстояние между соседними энергетическими уровнями может оказаться столь незначительным, что позволит считать функцию 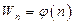 непрерывной (случай свободной микрочастицы).
непрерывной (случай свободной микрочастицы).
г) Квантование энергии электронов в водородоподобном атоме
В водородоподобном атоме вокруг ядра с электрическим зарядом, равным 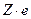 (где Z – порядковый номер химического элемента; e – заряд электрона), движется всего один – единственный электрон (предполагается, что отсутствие остальных
(где Z – порядковый номер химического элемента; e – заряд электрона), движется всего один – единственный электрон (предполагается, что отсутствие остальных 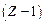 электронов в атоме обусловлено проявлением процессов ионизации). В этом случае, потенциальная энергия электростатического взаимодействия этого электрона с зарядом ядра равна (используется модельное представление согласно
электронов в атоме обусловлено проявлением процессов ионизации). В этом случае, потенциальная энергия электростатического взаимодействия этого электрона с зарядом ядра равна (используется модельное представление согласно
рис. 1.5,Б):
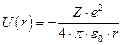 , ,
| (1.56) |
где 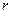 – расстояние между геометрическими центрами ядра и электрона;
– расстояние между геометрическими центрами ядра и электрона; 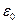 – электрическая постоянная, численно равная 8.854∙10-12 Ф/м.
– электрическая постоянная, численно равная 8.854∙10-12 Ф/м.
Поскольку рассматриваемая зарядовая система обладает центральной симметрией, уравнение Шредингера необходимо представить в сферической системе координат:
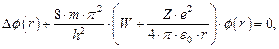
| (1.57) |
где 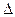 – оператор Лапласа, представленный в сферической системе
– оператор Лапласа, представленный в сферической системе
координат.
Решение уравнения (1.57) приводит к спектру разрешенных энергетических состояний для электрона в атоме в виде (подробный вывод рассмотрен в источнике [7]):
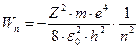 . .
| (1.58) |
Весьма характерно то обстоятельство, что фрагмент 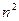 в выражении (1.58) находится в знаменателе (в выражении (1.55) он расположен в числителе). Это расхождение обусловлено тем обстоятельством, что в рассматриваемом случае не используется представление о бесконечной глубине потенциальной ямы, в которой находится микрочастица.
в выражении (1.58) находится в знаменателе (в выражении (1.55) он расположен в числителе). Это расхождение обусловлено тем обстоятельством, что в рассматриваемом случае не используется представление о бесконечной глубине потенциальной ямы, в которой находится микрочастица.
Решение в виде (1.58) является достаточно грубым приближением, поскольку в нем не учитывается фактор орбитального движения электрона, приводящего к нарушению сферической симметрии у функции плотности вероятности расположения электрона (обратить внимание на тот факт, что потенциальная функция (1.56) задана в симметричной форме относительно параметра r). Приемлемая точность выражения (1.58) имеет место только при значениях параметра n > 100.
Несмотря на оговоренные выше недостатки, выражение (1.58) нашло широкое распространение в научно-технической практике, поскольку оно способствует пониманию (на качественном уровне рассмотрения) физических принципов эффекта квантования энергии электронов в центрально-симметричных системах, в качестве которых выступают индивидуальные атомно-молекулярные объекты.
Рассмотренные выше примеры практического использования уравнения Шредингера позволяют понять основные методологические принципы квантово-механического анализа энергетического спектра состояний микрочастиц.
Следует отметить, что метод анализа состояния систем, основанный на использовании уравнения Шредингера, не является единственным в теоретическом арсенале квантовой механики. В частности, широкое распространение получил метод вторичного квантования [4], основанный на использовании (в качестве базовой концепции) операторов рождения и уничтожения элементарных квантовых состояний. Суть метода вторичного квантования состоит в том (подробное рассмотрение выходит за рамки настоящего пособия), что в нем, вместо волновых функций микрочастиц в координатном или в импульсном представлении (см. разд. 1.1.5) вводится в рассмотрение новый класс волновых функций в представлении чисел заполнения различных квантовых состояний одной частицы. При этом переходы между различными состояниями одной частицы описываются как уменьшение числа заполнения, соответствующего одной волновой функции, на единицу, и соответственного увеличения числа заполнения другого состояния на единицу.
Несомненным достоинством метода вторичного квантования является то, что он позволяет упростить процедуру анализа физико-технических функциональных (в плане практических интересов) систем, содержащих большое количество индивидуальных микрочастиц, используемых при формировании твердотельных микро- и наноразмерных атомно-молекулярных структур.
Дата добавления: 2016-01-03; просмотров: 1376;
