Энергетические состояния микрочастиц в наноразмерных структурах
а) Зонные энергетические диаграммы монокристаллических
структур
В разд. 1.1.7 на примере атома водородоподобного типа показано, что полная энергия микрочастицы (в частности, электрона), находящейся в потенциальной яме, квантуется. Последнее означает, что энергия микрочастицы может принимать ряд (в пределе бесконечный) строго определенных дискретных значений.
Рассмотрим вопрос: во что трансформируется спектр разрешенных энергетических состояний электрона, находящегося в атоме (потенциальной яме), при образовании кристаллического тела из большой совокупности индивидуальных атомов одного и того же типа. При этом следует иметь в виду то обстоятельство, что расстояние между соседними атомами в твердом теле настолько мало (порядка 1 ангстрем), что каждый атом находится в силовом поле, образованном соседними атомами. Несколько забегая вперед, отметим, что именно факт наличия оговоренного выше атомного силового поля вызывает трансформацию энергетических диаграмм (спектров) индивидуальных атомов при образовании ими кристаллических структур. В рамках настоящего раздела этот вопрос обсуждается на качественном уровне рассмотрения.
На рис. 1.7 представлены энергетические диаграммы и волновые функции 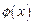 для случая двух однотипных атомов, разнесенных друг от друга на столь значительное расстояние r, что их атомные силовые поля можно считать не взаимодействующими.
для случая двух однотипных атомов, разнесенных друг от друга на столь значительное расстояние r, что их атомные силовые поля можно считать не взаимодействующими.
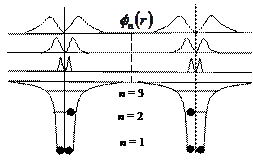
Рис. 1.7. Амплитудные волновые функции электронов при n = 1, 2, 3
для двухатомной системы (случай отсутствия взаимодействия атомных полей)
Для дальнейшего рассмотрения вопроса необходимо отметить ряд характерных деталей (рис. 1.7):
· атомные потенциальные функции 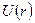 пространственно разнесены и в этой связи не претерпевают искажений, обусловленных присутствием соседнего атома;
пространственно разнесены и в этой связи не претерпевают искажений, обусловленных присутствием соседнего атома;
· посредством горизонтальных отрезков, расположенных в потенциальной яме, отображены разрешенные энергетические состояния (уровни) электронов в атоме;
· чем глубже расположен электрон в потенциальной яме (например: при n = 1), тем он более локализован в пространстве (т.е. более несвободен в своем движении);
· при очень больших значениях параметра n разрешенные энергетические состояния подходят близко к потолку потенциальной ямы и волновые функции 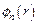 становятся все более протяженными, а следовательно, поведение электрона приобретает черты свободного движения микрочастиц (т.е. волн де Бройля);
становятся все более протяженными, а следовательно, поведение электрона приобретает черты свободного движения микрочастиц (т.е. волн де Бройля);
· суперпозиция всевозможных амплитудных волновых функций 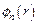 при значениях параметра n = 1, 2, 3,∙∙∙, ∞ образует волновой пакет, реализующий фактор локализации микрочастицы в пределах потенциального ящика (атома);
при значениях параметра n = 1, 2, 3,∙∙∙, ∞ образует волновой пакет, реализующий фактор локализации микрочастицы в пределах потенциального ящика (атома);
· жирными точками условно обозначено положение электронов, находящихся на разрешенных энергетических уровнях (согласно принципу Паули их должно быть не более двух на одном энергетическом уровне).
Сблизим теперь атомы друг к другу до такого малого расстояния, чтобы их атомные поля начали перекрываться, и рассмотрим возможные варианты заселения энергетических уровней имеющимися у атомов электронами (в данном случае это шесть электронов, отображенных на рис. 1.7). Здесь надо иметь в виду то обстоятельство, что если ранее имели место два независимых объекта (атомов), то теперь имеется одна общая атомная система, подчиняющая «интересы» индивидуальных атомов «интересам» системы в целом.
Под последним утверждением понимается то фундаментальное
обстоятельство, что любая физическая система в процессе ее самопроизвольной эволюции стремится в конечном итоге принять состояние, обладающее минимальной энергией. (В более строгой постановке, здесь следует говорить о выполнении принципа минимальной свободной энергии системы, который является своеобразным компромиссом между принципами минимальной энергии и максимальной энтропии системы [6]).
На рис. 1.8 рассмотрены возможные варианты трансформации энергетической диаграммы индивидуальных атомов при образовании ими кристаллической структуры.
В первом варианте «сложения» энергетических спектров индивидуальных атомов (на рис. 1.8 – зачеркнут) энергетическая диаграмма оставлена неизменной, и электроны при образовании кристаллической структуры начинают заполнять более высоко отстоящие свободные энергетические уровни (напомним, что согласно принципу Паули, на каждом энергетическом уровне может быть расположено не более двух электронов). Но в этом случае, при большом количестве атомов, образующих кристалл (в 1 см3 кристалла порядка 1023 атомов), электроны начнут заполнять энергетические уровни, весьма близко отстоящие от нулевого уровня «0», в результате чего работа выхода электронов из кристалла становится функцией размера образуемого кристалла. Поскольку на практике это свойство кристалла не проявляется, рассмотренный вариант энергетической диаграммы является ошибочным.

Рис. 1.8. Схематическое отображение трансформации энергетического спектра
состояний электронов при образовании кристалла
(Wвых – работа (энергия) выхода электрона из кристалла)
В действительности, в природе наблюдается ситуация, представленная на рис. 1.8 справа. Ей соответствует тот факт, что при объединении атомов в кристаллическую структуру каждый индивидуальный энергетический уровень атома расщепляется на совокупность 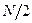 дополнительных уровней, где
дополнительных уровней, где 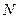 – количество атомов, задействованных в процессе создания кристалла.
– количество атомов, задействованных в процессе создания кристалла.
Для дальнейшего рассмотрения важно акцентировать внимание на трех принципиальных моментах:
· при образовании кристалла каждый энергетический уровень электрона в атоме вырождается в энергетическую зону, содержащую большое количество ( 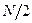 ) разрешенных энергетических состояний и имеющую протяженность (по энергетической шкале исчисления) порядка 1 эВ;
) разрешенных энергетических состояний и имеющую протяженность (по энергетической шкале исчисления) порядка 1 эВ;
· расстояние между соседними уровнями в энергетической зоне составляет по порядку величины – 10-23 эВ. Столь малое значение энергетического интервала позволяет считать, что энергетический спектр разрешенных состояний в пределах разрешенной энергетической зоны является (практически) непрерывным, а не дискретным, как это имеет место в индивидуальных атомах. (Для сравнения отметим, что средняя тепловая энергия микрочастицы, приходящаяся на одну степень свободы, составляет (при температуре окружающей среды T = 300 K) 0.025 эВ. Приведенное значение средней тепловой энергии более чем на двадцать порядков превышает энергетический интервал между соседними уровнями, расположенными в пределах разрешенной энергетической зоны кристалла. В этой связи при рассмотрении макроскопических тел дискретный характер энергетического спектра в разрешенной энергетической зоне практически не проявляется;
· значительная протяженность (1 эВ) энергетических зон при относительно небольшой полной глубине атомной потенциальной ямы
(2 – 28 эВ), как правило, приводит к эффекту перекрытия зон, т.е. к их наложению друг на друга, что еще больше способствует образованию непрерывного спектра допустимых энергетических состояний, но уже в пределах объединенных зон.
Появление энергетических зон в кристаллических структурах существенным образом сказывается на их электрических и оптических характеристиках, что и обуславливает практический интерес к этому вопросу. На рис. 1.9 представлена обобщенная энергетическая диаграмма фрагмента кристаллической структуры, построенная с учетом моментов, приведенных на рис. 1.7 и 1.8.
Уточним и конкретизируем ряд характерных графических фрагментов, представленных на рис. 1.9:
· посредством штриховки отображены факторы наличия дискретных энергетических уровней и конечной протяженности (по энергетической шкале) индивидуальной энергетической зоны кристаллической структуры, соответствующей определенному значению квантового числа n;
· точками, расположенными в пределах энергетической зоны, отражен тот факт, что в данной зоне индивидуальные энергетические уровни могут быть полностью либо частично заполнены электронами;
· точка «А» характеризует местоположение максимального значения потенциальной энергии кристаллической системы, имеющей периодический характер по пространственной координате x (рассматривается одномерный случай);
· штриховая линия на верхнем фрагменте графика функции 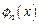 отображает суммарное значение амплитудной волновой функции в пределах этого интервала (в рамках модельного представления о суперпозиции индивидуальных вероятностных волн де Бройля, характерных для свободной частицы);
отображает суммарное значение амплитудной волновой функции в пределах этого интервала (в рамках модельного представления о суперпозиции индивидуальных вероятностных волн де Бройля, характерных для свободной частицы);
· функция потенциальной энергии (в нижней части рисунка) претерпела значительное изменение относительно невозмущенной функции потенциальной энергии (см. рис. 1.7), что обусловлено фактором сильного сближения соседних атомов (до расстояния порядка 1 ангстрем) в процессе образования кристаллической структуры.


Рис. 1.9. Схематическое отображение энергетических зон в кристалле
и соответствующих им амплитудных волновых функций 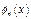
На основании схематического отображения, представленного на
рис. 1.9, можно сформулировать ряд важных, с практической точки зрения, выводов относительно характера поведения электронов, находящихся в атомных структурах с периодической потенциальной функцией:
· амплитудные волновые функции электронов, расположенных в глубоко лежащих энергетических зонах (n = 1), имеют ярко выраженный локализованный характер, а следовательно, возможность их перемещения в пределах кристаллической структуры полностью исключается (т.е. их следует считать абсолютно несвободными с позиции представлений о ПМВ де Бройля);
· электроны, находящиеся в энергетической зоне, условно характеризуемой квантовым числом n = 2, имеют более протяженные в пространстве амплитудные волновые функции и для них существует определенная вероятность движения в пределах кристаллической структуры (т.е. их следует считать ограниченно свободными с позиции представлений о ПМВ де Бройля);
· электроны, находящиеся в энергетической зоне, условно характеризуемой квантовым числом n = 3 (обратить внимание на штриховую линию на фрагменте амплитудной волновой функции), могут рассматриваться как свободные микрочастицы, движение которых полностью соответствует поведению элементарных ПМВ де Бройля.
Для полноты рассмотрения необходимо отметить, что согласно
рис. 1.9 взаимное расположение атомов принято статичным, т.е. предполагается, что межатомное расстояние является неизменной величиной. В реальности же наличие фактора теплового колебательного движения атомов (получивших название фононов) приводит к появлению вариаций этого расстояния, а следовательно, положение точки А на энергетической шкале (см. рис. 1.9) тоже непрерывно меняется (происходит ее перемещение вверх или вниз) во времени. В этой связи амплитудные волновые функции испытывают аналогичные динамические вариации, что может внести свои негативные коррективы в характер движения электронов (в частности может иметь место рассеяние поступательного движения электронов на фононах). Представляется очевидным, что интенсивность процессов рассеяния поступательного движения электронов в кристаллической структуре должна подчиняться общим статистическим закономерностям процессов образования фононов.
Энергетическая диаграмма, представленная на рис. 1.9, не используется в современной инженерно-физической практике, поскольку она обременена большим количеством деталей. На практике используется гораздо более лаконичное отображение, получившее название зонной диаграммы кристаллической структуры, представленное на рис. 1.10.


Рис.1.10. Зонные энергетические диаграммы кристаллических структур
Для построения зонной диаграммы (рис. 1.10) используются следующие фрагменты рис. 1.9:
· самая высоко расположенная энергетическая зона, заполненная электронами (n = 2, на рис. 1.9), – валентная зона;
· самая низко расположенная энергетическая зона, свободная от электронов при температуре кристалла равной нулю (n = 3, на рис.1.9), – зона проводимости;
· интервал между вышеуказанными зонами – запрещенная зона.
На рис. 1.10 использованы символы, нашедшие широкое распространение в современной научно-технической практике:
· Wc – значение энергии для самого низко расположенного энергетического уровня в зоне проводимости;
· Wv – значение энергии для самого высоко расположенного энергетического уровня в валентной зоне;
· ∆W – ширина запрещенной зоны.
Несмотря на лаконичность рассмотренной зонной диаграммы,
ее вполне достаточно для объяснения практически всех электрофизических и оптических характеристик кристаллических структур с электронным типом проводимости. В частности, с ее помощью проводится классификация кристаллических тел по критерию их электропроводности: ∆W = 0 – металлы (энергетические зоны перекрываются);
∆W < 1.5 эВ – собственные полупроводники; ∆W > 1.5 эВ – диэлектрики. Из приведенного принципа классификации веществ по критерию их уровня электропроводности следует, что разделение материалов на диэлектрики и полупроводники имеет несколько условный характер.
б) Спектр энергетических состояний в рамках модели
слабосвязанных электронов
В вышеизложенном пункте (а) настоящего раздела проведен анализ (на качественном уровне рассмотрения) энергетических диаграмм конденсированных сред, что позволило уяснить основные физические принципы появления практически непрерывных энергетических спектров разрешенных состояний микрочастиц в регулярных многоатомных структурах и целесообразность их отображения в виде зонных энергетических диаграмм. Ниже этот же круг вопросов будет рассмотрен более корректно, с использованием математического аппарата волновой квантовой механики.
Последующий анализ проводится в рамках модели, основанной (в целях упрощения математических выкладок) на приближении слабосвязанных электронов [7]. Согласно этому приближению, потенциальная диаграмма кристаллической структуры представляется в виде потенциального ящика со слаборифленым дном, отражающим периодический характер функции потенциальной энергии электрона в кристаллической структуре. При этом считается, что потенциал решетки мало отличается от потенциала решетки в приближении свободных электронов. Последнее приближение можно допустить в случае, если глубина потенциального ящика намного превышает амплитуду рифления дна ящика.
Привлекательность приближения слабосвязанных электронов состоит в том, что в этом случае представляется возможным искать решение уравнения Шредингера (1.34а) в виде совокупности элементарных ПМВ де Бройля. Однако следует иметь в виду то обстоятельство, что периодические вариации потенциальной энергии (рифление дна ящика) должны найти свое отражение в общем решении уравнения Шредингера. Представляется вполне естественным, что указанная периодичность потенциала в кристаллической структуре должна привести к появлению фактора дополнительной периодичности амплитудной волновой функции 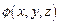 .
.
С учетом вышеизложенных моментов амплитудная волновая функция электрона, находящегося в периодическом потенциале, ищется в виде выражения (для одномерного случая)
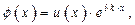
| (1.59) |
где 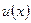 – некоторая периодическая функция с периодом, равным постоянной (межцентровому расстоянию между соседними атомами) кристаллической структуры.
– некоторая периодическая функция с периодом, равным постоянной (межцентровому расстоянию между соседними атомами) кристаллической структуры.
Выражение (1.59) в современной научно-технической практике
получило название функции Блоха. Нетрудно заметить, что по своей сути функция Блоха представляет собой рассмотренную ранее ПМВ
де Бройля (фрагмент 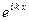 ), амплитуда которой модулирована периодической функцией
), амплитуда которой модулирована периодической функцией 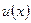 . Конкретный вид функции
. Конкретный вид функции 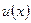 определяется видом периодической потенциальной функции кристаллической структуры
определяется видом периодической потенциальной функции кристаллической структуры 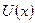 , используемой в уравнении Шредингера.
, используемой в уравнении Шредингера.
На рис. 1.11 представлена потенциальная функция кристаллической структуры (модель Кронига-Пенни), которая будет использована в дальнейшем для нахождения спектра разрешенных энергетических состояний в регулярной кристаллической структуре.
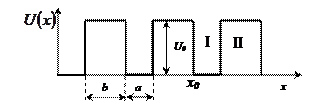

Рис. 1.11. Фрагмент потенциальной диаграммы кристаллической структуры
в рамках модели Кронига-Пенни
Допустим, что энергия электрона W меньше высоты потенциального барьера U0 (в этом случае можно считать, что он заперт в ограниченных пределах потенциального ящика с рифленым дном). В общем случае состояние электрона (амплитудная волновая функция) описывается уравнением Шредингера (см. (1.34а)):
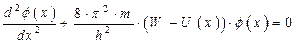 . .
| (1.60) |
Для областей (I), для которых 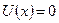 , решение уравнения Шредингера (1.60) имеет вид (подробнее см. раздел № 1.1.7, пункт «б»)
, решение уравнения Шредингера (1.60) имеет вид (подробнее см. раздел № 1.1.7, пункт «б»)
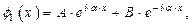
| (1.61) |
где A и B – постоянные коэффициенты; 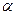 – характеристический
– характеристический
параметр движения микрочастицы в области (I), равный 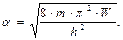
Для областей (II), для которых 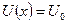 , решение уравнения Шредингера (1.60) имеет вид (подробнее см. раздел № 1.1.7, пункт «в»)
, решение уравнения Шредингера (1.60) имеет вид (подробнее см. раздел № 1.1.7, пункт «в»)
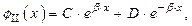
| (1.62) |
где C и D – постоянные коэффициенты; 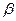 – характеристический
– характеристический
параметр движения микрочастицы в области (II), равный 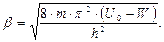
Подставив амплитудные волновые функции 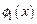 и
и 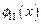 из выражений (1.61) и (1.62) в выражение для функции Блоха (1.59), можно определить вид периодической функции
из выражений (1.61) и (1.62) в выражение для функции Блоха (1.59), можно определить вид периодической функции 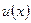 для соответствующих пространственных областей (I) и (II):
для соответствующих пространственных областей (I) и (II):
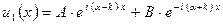 ; ;
| (1.63) | |
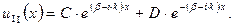
| (1.64) |
Для определения постоянных коэффициентов A, B, C и D воспользуемся условиями:
· Условие № 1: Функция 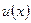 и ее первая производная считаются непрерывными, в том числе в местах скачка потенциальной энергии (например в точке x0), поскольку реальные природные объекты не имеют бесконечных скоростей в процессах эволюции:
и ее первая производная считаются непрерывными, в том числе в местах скачка потенциальной энергии (например в точке x0), поскольку реальные природные объекты не имеют бесконечных скоростей в процессах эволюции:
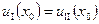 ; ; 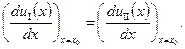
| (1.65) |
· Условие № 2: Функция 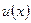 обладает свойством периодичности по геометрическим координатам с периодом, равным (a+b):
обладает свойством периодичности по геометрическим координатам с периодом, равным (a+b):
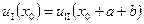 ; ; 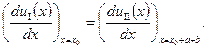
| (1.66) |
Подставив в (1.65) и (1.66) функции 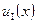 и
и 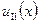 (согласно выражениям (1.63) и (1.64)), получим систему из четырех уравнений, необходимых для определения значений постоянных коэффициентов: A, B, C, D. Чтобы рассматриваемая система уравнений имела решения для указанных коэффициентов A, B, C, D, отличные от нуля, необходимо, чтобы определитель системы уравнений был равен нулю. Последнее требование приводит к уравнению
(согласно выражениям (1.63) и (1.64)), получим систему из четырех уравнений, необходимых для определения значений постоянных коэффициентов: A, B, C, D. Чтобы рассматриваемая система уравнений имела решения для указанных коэффициентов A, B, C, D, отличные от нуля, необходимо, чтобы определитель системы уравнений был равен нулю. Последнее требование приводит к уравнению
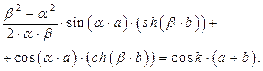 
| (1.67) |
В целях упрощения дальнейшего анализа рассмотрим широко используемый предельный частный случай, в котором:
· ширина атомного потенциального барьера 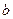 (согласно рис. 1.11) устремляется к нулю (
(согласно рис. 1.11) устремляется к нулю (  );
);
· высота атомного потенциального барьера синхронно устремляется к бесконечности (  ), причем таким образом, чтобы произведение
), причем таким образом, чтобы произведение 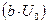 оставалось постоянной величиной (некий аналог дельта-функции).
оставалось постоянной величиной (некий аналог дельта-функции).
Введем в рассмотрение характеристический параметр 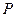 – прозрачность потенциального барьера для реализации процесса движения микрочастицы по периодической структуре согласно рис. 1.11:
– прозрачность потенциального барьера для реализации процесса движения микрочастицы по периодической структуре согласно рис. 1.11:
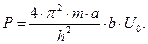 
| (1.68) |
С учетом сделанных упрощений (  ;
; 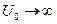 ) и использованием (1.68) выражение (1.67) преобразуется к виду
) и использованием (1.68) выражение (1.67) преобразуется к виду
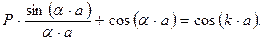 
| (1.69) |
Выражение (1.69) отражает в неявном виде зависимость энергии электрона W (которая входит в состав параметра 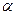 , см. выражение (1.61)) от волнового вектора k и прозрачности потенциального барьера P.
, см. выражение (1.61)) от волнового вектора k и прозрачности потенциального барьера P.
На рис. 1.12 представлено графическое решение уравнения (1.69). По оси абсцисс отложен комплексный параметр ( 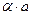 ), а по оси ординат – фрагмент выражения (1.69):
), а по оси ординат – фрагмент выражения (1.69):
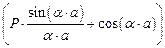 .
.
Поскольку функция 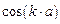 , стоящая в правой части выражения (1.69), не может быть (по определению) больше +1 и меньше -1,
, стоящая в правой части выражения (1.69), не может быть (по определению) больше +1 и меньше -1,
то параметр ( 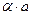 ) может принимать только такие значения, при которых левая часть уравнения (1.69) не может выходить за пределы значений ±1.
) может принимать только такие значения, при которых левая часть уравнения (1.69) не может выходить за пределы значений ±1.
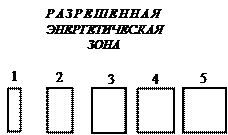
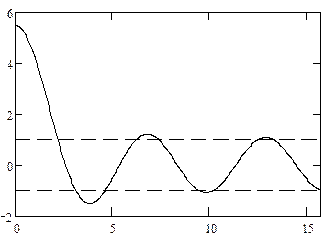
Рис. 1.12. Схематическое отображение процесса образования энергетических зон
в структуре с периодической потенциальной энергией
Из рис. 1.12 следует, что вся шкала энергий (ось абсцисс) разделяется на ряд дискретных интервалов:
· разрешенные энергетические зоны, в которых значения энергий лежат в интервалах, ограниченных прямоугольниками;
· запрещенные энергетические зоны, в которых значения энергий лежат в интервалах, составляющих промежутки между прямоугольниками.
С увеличением энергии электрона (т.е. параметра ( 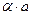 )) ширина разрешенных энергетических зон увеличивается, а ширина запрещенных зон уменьшается.
)) ширина разрешенных энергетических зон увеличивается, а ширина запрещенных зон уменьшается.
Как и следовало ожидать, ширина разрешенных и запрещенных энергетических зон является функцией прозрачности потенциального барьера P. При выполнении условия 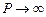 разрешенные зоны сужаются, превращаясь в дискретные уровни, соответствующие условию
разрешенные зоны сужаются, превращаясь в дискретные уровни, соответствующие условию 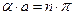 , где параметр n = ±1, ±2,…, т.е. к значениям энергий, соответствующим изолированной потенциальной яме. При выполнении условия
, где параметр n = ±1, ±2,…, т.е. к значениям энергий, соответствующим изолированной потенциальной яме. При выполнении условия 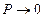 возникает противоположная ситуация, при которой исчезают запрещенные зоны и движение электрона становится практически свободным (аналог ПМВ де Бройля).
возникает противоположная ситуация, при которой исчезают запрещенные зоны и движение электрона становится практически свободным (аналог ПМВ де Бройля).
Согласно вышеизложенным моментам, внутри каждой разрешенной энергетической зоны (см. рис. 1.12) энергия электрона непрерывно возрастает с увеличением волнового вектора k. При значениях последнего, равных
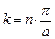 ; (n = ±1, ±2, …), ; (n = ±1, ±2, …),
| (1.70) |
энергия электронов претерпевает разрыв, приводящий к появлению на энергетической диаграмме запрещенных зон (для преемственности анализа сравнить с материалами раздела 1.1.7,в).
Принимая во внимание, что волновой вектор 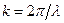 , выражение (1.70) можно преобразовать к более явному виду с позиции представлений о ПМВ де Бройля и заодно получить известную формулу Вульфа-Брегга, выражающую условие дифракции волн де Бройля для случая, когда угол падения электронного луча на плоскость кристаллической решетки равен 90°:
, выражение (1.70) можно преобразовать к более явному виду с позиции представлений о ПМВ де Бройля и заодно получить известную формулу Вульфа-Брегга, выражающую условие дифракции волн де Бройля для случая, когда угол падения электронного луча на плоскость кристаллической решетки равен 90°:
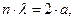 (n = ±1, ±2, ∙∙∙). (n = ±1, ±2, ∙∙∙).
| (1.71) |
Для последующего рассмотрения важно отметить, что зависимость 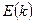 вблизи нижней и верхней границ разрешенной зоны является квадратичной функцией волнового вектора, отсчитанного от численного значения этой границы [7]:
вблизи нижней и верхней границ разрешенной зоны является квадратичной функцией волнового вектора, отсчитанного от численного значения этой границы [7]:
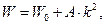
| (1.72) |
где 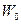 – энергия, соответствующая границе зоны; А – постоянный коэффициент.
– энергия, соответствующая границе зоны; А – постоянный коэффициент.
У дна разрешенной зоны парабола (1.72) является нормальной –
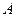 > 0, а у потолка зоны парабола является обращенной –
> 0, а у потолка зоны парабола является обращенной – 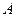 < 0 (подробный анализ этого вопроса выходит за рамки настоящего пособия и приведен в источнике [8]).
< 0 (подробный анализ этого вопроса выходит за рамки настоящего пособия и приведен в источнике [8]).
в) Изоэнергетические поверхности состояния электронов
в кристаллических структурах
На рис. 1.12 представлено графическое отображение зависимости энергии электронов от волнового вектора, испытывающего вариации значений от 0 до ±∞ (на рисунке изображена только положительная ветвь (!)). Периодический характер поведения волнового вектора (см. выражение (1.70)) позволяет выразить энергию электронов, находящихся в различных разрешенных энергетических зонах, с помощью волновых векторов, лежащих в пределах первой зоны, т.е. принимающих значения в интервале от 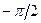 до
до 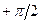 . Эта процедура представляется тем более возможной, если учесть тот факт, что выражению (1.60) удовлетворяет не только функция
. Эта процедура представляется тем более возможной, если учесть тот факт, что выражению (1.60) удовлетворяет не только функция 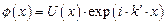 , где
, где 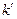 – волновой вектор, лежащий в пределах первой зоны, но и функция
– волновой вектор, лежащий в пределах первой зоны, но и функция 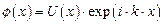 , где вектор
, где вектор 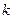 , отображающий состояние электронов в любой другой энергетической зоне под номером
, отображающий состояние электронов в любой другой энергетической зоне под номером 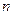 (см. рис 1.12.), удовлетворяет условию
(см. рис 1.12.), удовлетворяет условию
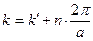 . .
| (1.73) |
Процедура построения всех энергетических зон в пределах первой энергетической зоны называется приведением зон, а сами зоны – приведенными зонами. Смысл процедуры приведения энергетических зон состоит в перемещении фрагментов зависимости функции 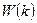 , относящихся к различным зонам, к отрезку оси энергии с координатами
, относящихся к различным зонам, к отрезку оси энергии с координатами 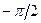 и
и 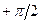 .
.
На рис. 1.13 представлено схематическое отображение функций 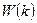 , приведенных в нормальном (сплошные линии) и приведенном (пунктирные линии) виде. Штрихпунктирной линией изображена зависимость
, приведенных в нормальном (сплошные линии) и приведенном (пунктирные линии) виде. Штрихпунктирной линией изображена зависимость 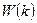 для случая свободного электрона (см. выражение (1.15)). Из рисунка следует, что у всех зон с нечетными значениями параметра n в центре расположены минимумы энергии, а с четными значениями n – максимумы энергии. Характерным моментом энергетической диаграммы является увеличение ширины разрешенных зон и уменьшение ширины запрещенных зон с возрастанием волнового вектора k , что нашло свое отражение на фрагменте, расположенном справа на рис. 1.13 для частных случаев n = 1, 2, 3.
для случая свободного электрона (см. выражение (1.15)). Из рисунка следует, что у всех зон с нечетными значениями параметра n в центре расположены минимумы энергии, а с четными значениями n – максимумы энергии. Характерным моментом энергетической диаграммы является увеличение ширины разрешенных зон и уменьшение ширины запрещенных зон с возрастанием волнового вектора k , что нашло свое отражение на фрагменте, расположенном справа на рис. 1.13 для частных случаев n = 1, 2, 3.
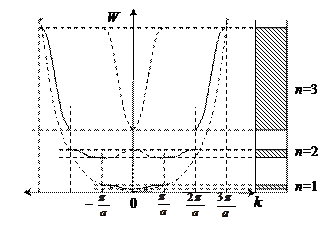

Рис. 1.13. Схематическое отображение функций 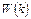 , представленных
, представленных
в нормальном (сплошные линии) и приведенном (пунктирные линии) виде
Приведенные выше материалы могут быть распространены и на трехмерный случай, характерный для реальных кристаллических структур. Так как параметры решетки (т.е. периодичности), как правило, не одинаковы по разным направлениям в кристалле, то и значения волнового вектора 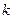 , при которых наступают разрывы в разрешенных энергетических зонах, будут также различны (см. выражение (1.70)):
, при которых наступают разрывы в разрешенных энергетических зонах, будут также различны (см. выражение (1.70)):
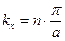 ; ; 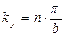 ; ; 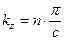 , (n = ±1, ±2, ∙∙∙), , (n = ±1, ±2, ∙∙∙),
| (1.74) |
где a, b, c – параметры кристаллической решетки соответственно по координатным направлениям x, y, z.
По аналогии с (1.73), для трехмерной кристаллической структуры вблизи дна разрешенной зоны, характеризуемой нечетными значениями параметра n = 1, 3, для функции 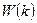 имеем
имеем
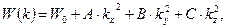
| (1.75) |
где W0 – энергия электрона, соответствующая местоположению дна разрешенной зоны; A, B, C – постоянные коэффициенты, которые в случае минимума (т.е. нечетных значений параметра n) являются положительными величинами.
Для кристаллов кубического типа, в которых ввиду симметрии
A = B = C, выражение (1.75) трансформируется к виду
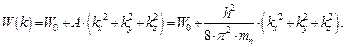
| (1.76) |
В выражении (1.76) постоянный коэффициент А представлен в виде, аналогичном случаю движения свободного электрона (см. выражение (1.15)), с тем лишь отличием, что масса свободного электрона заменена на эффективную массу электрона, значение которой характерно для каждого конкретного типа кристаллической структуры.
Для четных значений параметра n (в центре приведенной зоны находится максимум энергии) функция 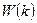 также определяется с помощью выражений (1.75) и (1.76), однако в этом случае постоянные коэффициенты A, B, C являются отрицательными величинами. Интересно отметить, что для этого случая и эффективная масса электрона mn также приобретает отрицательное значение, в силу того что фрагмент
также определяется с помощью выражений (1.75) и (1.76), однако в этом случае постоянные коэффициенты A, B, C являются отрицательными величинами. Интересно отметить, что для этого случая и эффективная масса электрона mn также приобретает отрицательное значение, в силу того что фрагмент 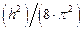 в выражении (1.76) является положительной величиной. Физическая сущность и вытекающие практические следствия из этого парадоксального феномена рассмотрены в источнике [7].
в выражении (1.76) является положительной величиной. Физическая сущность и вытекающие практические следствия из этого парадоксального феномена рассмотрены в источнике [7].
Поверхность в координатном представлении {kx, ky, kz}, отображающая энергетическое состояние системы и удовлетворяющая условию 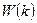 = const, называется изоэнергетической поверхностью. С учетом вышеизложенных моментов изоэнергетические поверхности в пространстве состояний {kx, ky, kz}, в общем случае имеют вид эллипсоидов вращения (согласно выражению (1.75)), а в частном случае, для кристаллических структур кубического типа,– сферический вид (согласно выражению (1.76)).
= const, называется изоэнергетической поверхностью. С учетом вышеизложенных моментов изоэнергетические поверхности в пространстве состояний {kx, ky, kz}, в общем случае имеют вид эллипсоидов вращения (согласно выражению (1.75)), а в частном случае, для кристаллических структур кубического типа,– сферический вид (согласно выражению (1.76)).
На рис. 1.14 представлены характерные примеры отображения изоэнергетических поверхностей кристаллических структур.
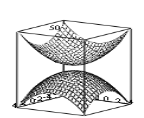
| 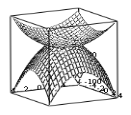
|
| Навырожденный случай (полупроводник) | Вырожденный случай (металл) |
Рис. 1.14. Изоэнергетические поверхности состояния электрона
(квантовые числа n = 2 и 3 выбраны согласно рис. 1.13)
При этом следует иметь в виду то обстоятельство, что экстремумы функции 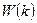 не обязательно должны располагаться в центрах приведенных энергетических зон, поскольку последнее имеет место лишь в том случае, если граничные значения волновых векторов kx, ky, kz в пределах индивидуальных зон имеют одинаковые величины.
не обязательно должны располагаться в центрах приведенных энергетических зон, поскольку последнее имеет место лишь в том случае, если граничные значения волновых векторов kx, ky, kz в пределах индивидуальных зон имеют одинаковые величины.
г) Спектр энергетических состояний в наноразмерных структурах
типа (0D)
В наноразмерных структурах типа (0D) движение электронов ограничено по всем трем координатным направлениям. Эти ограничения соответствуют случаю нахождения микрочастицы в трехмерном потенциальном ящике, который имеет весьма малую протяженность по всем координатным осям – {x, y, z}. В современной научно-технической практике диапазон этой протяженности сопоставим с интервалом значений характеристических длин порядка 1 – 100 нм. Именно исходя из этого обстоятельства такие структуры получили название квантовой точки, несмотря на то что они могут содержать достаточно большое количество атомов.
На рис. 1.15 представлено модельное отображение квантовой точки с позиции общих представлений о трехмерном потенциальном ящике.
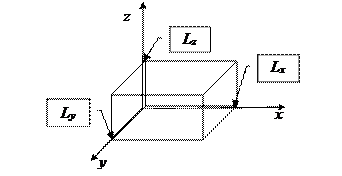

Рис. 1.15. Пространственное отображение квантовой точки
с характеристическими размерными параметрами { 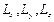 }
}
Беря за основу одномерную модель потенциального ящика (см. выражение (1.55)), для функции 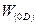 применительно к квантовой точке в общем случае имеем
применительно к квантовой точке в общем случае имеем
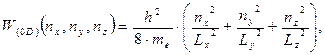
| (1.77) |
где 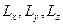 – пространственная протяженность квантовой точки соответственно по координатным направлениям {x, y, z};
– пространственная протяженность квантовой точки соответственно по координатным направлениям {x, y, z}; 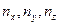 – квантовые числа из набора целочисленных величин {1, 2, …, ∞}, характеризующие локальное состояние микрочастицы соответственно по координатным направлениям {x, y, z}.
– квантовые числа из набора целочисленных величин {1, 2, …, ∞}, характеризующие локальное состояние микрочастицы соответственно по координатным направлениям {x, y, z}.
Для квантовой точки кубического типа (т.е. при выполнении условия 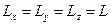 ) выражение (1.77) трансформируется к более симметричному виду:
) выражение (1.77) трансформируется к более симметричному виду:
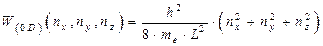 . .
| (1.78) |
Из выражений (1.77) и (1.78) следует, что энергия электронов, находящихся в пределах квантовой точки, может принимать только ряд дискретных значений, разделенных друг от друга конечными интервалами энергии. Этот феномен дискретизации значений энергии электронов, находящихся в квантовой точке наглядно представлен на рис. 1.16 с помощью двумерного отображения энергетического состояния электронов.


Рис. 1.16. Схематическое отображение
фактора дискретизации энергии электронов в квантовой точке
({W (1,2): nx = 1;ny = 2}; {W (2,1): nx = 2;ny = 1})
Выражение (1.78) свидетельствует о возможности появления в квантовых точках кубического типа вырожденных энергетических состояний, обусловленных вариациями значений совокупности квантовых чисел { 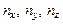 } при одновременном выполнении условия
} при одновременном выполнении условия 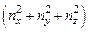 = const.
= const.
Энергетические спектры (1.77) и (1.78) можно представить как функциональные зависимости от волновых векторов. Для этого воспользуемся представлением (согласно рис. 1.3) 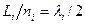 и определением волнового вектора
и определением волнового вектора 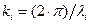 , где параметр
, где параметр 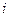 относится к геометрическим координатам {x, y, z}. После очевидных преобразований получим выражение
относится к геометрическим координатам {x, y, z}. После очевидных преобразований получим выражение 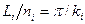 , на основании которого преобразуем выражение (1.77) к виду
, на основании которого преобразуем выражение (1.77) к виду
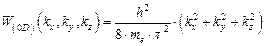 , ,
| (1.79) |
где волновые векторы {kx, ky, kz} могут принимать строго фиксированные численные значения, соответствующие квантовым числам { 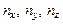 }.
}.
Интересно отметить, что выражение (1.79) справедливо в одинаковой мере к любым квантовым точкам, независимо от их геометрической конфигурации (в отличие от представления, основанного на квантовых числах).
Важным аспектом при проведении физико-химического анализа наноразмерных систем является функция плотности квантовых состояний электронов. По определению, плотность квантовых состояний 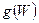 – отношение количества квантовых состояний
– отношение количества квантовых состояний 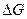 , приходящихся на малый интервал энергий
, приходящихся на малый интервал энергий 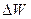 (в пределе бесконечно малый), к величине этого энергетического интервала
(в пределе бесконечно малый), к величине этого энергетического интервала 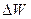 :
: 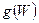 =
= 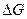 /
/ 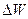 . В частности, функция
. В частности, функция 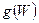 необходима для определения концентрации носителей зарядов в связи с рассмотрением вопроса электропроводности в наноразмерных системах.
необходима для определения концентрации носителей зарядов в связи с рассмотрением вопроса электропроводности в наноразмерных системах.
Применительно к наноразмерным системам типа (0D) функция плотности квантовых состояний электронов имеет вид [5]
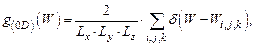
| (1.80) |
где индексы 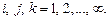
На рис. 1.17 представлено графическое отображение функции плотности квантовых состояний 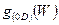 , характерной для наноразмерной структуры типа квантовой точки.
, характерной для наноразмерной структуры типа квантовой точки.
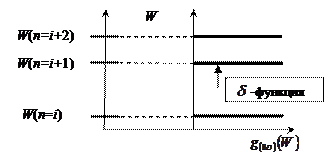
Рис.1.17. Функция плотности квантовых состояний для случая квантовой точки
(правый фрагмент) и соответствующий ей спектр разрешенных квантовых состояний (левый фрагмент)
Присутствие в выражении (1.80) 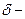 функции весьма характерно и свидетельствует о том, что энергетический спектр электронов представляет собой совокупность индивидуальных дискретных квантовых состояний. Именно благодаря подобному сходству энергетических спектров индивидуальных атомов и квантовых точек, эти наноразмерные структуры в ряде практических случаев называются искусственными атомами.
функции весьма характерно и свидетельствует о том, что энергетический спектр электронов представляет собой совокупность индивидуальных дискретных квантовых состояний. Именно благодаря подобному сходству энергетических спектров индивидуальных атомов и квантовых точек, эти наноразмерные структуры в ряде практических случаев называются искусственными атомами.
д) Спектр энергетических состояний в наноразмерных структурах
типа (1D)
В наноразмерных структурах типа (1D) движение электронов ограничено по двум координатным направлениям. Эти ограничения соответствуют случаю нахождения микрочастицы в трехмерном потенциальном ящике, который имеет весьма малую протяженность по двум координатным осям {y, z}. В современной научно-технической практике диапазон этой протяженности так же, как было уже изложено выше, сопоставим с интервалом значений характеристических длин порядка
1 – 100 нм. Именно исходя из этого обстоятельства такие структуры получили название квантовой проволоки (нити, шнура). Квантовые проволоки, как и квантовые точки, могут содержать в своем составе достаточно большое (в пределе бесконечное, при бесконечной протяженности проволоки) количество атомов.
На рис. 1.18 представлено модельное отображение квантовой проволоки с позиции общих представлений о трехмерном, протяженном в направлении одной из координат потенциальном ящике. Беря за основу анализа одномерную модель потенциального ящика для координатных направлений {y, z} (см. выражение (1.55)) и модельное представление о движении свободного электрона по координатному направлению {x} (см. выражение (1.15)), для функции 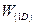 применительно к квантовой проволоке имеем (сравнить приводимое выражение с (1.77)):
применительно к квантовой проволоке имеем (сравнить приводимое выражение с (1.77)):
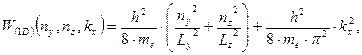
| (1.81) |
где me – эффективная масса электрона при его поступательной форме движения по координатному направлению {x}; 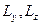 – пространственная протяженность квантовой точки соответственно по координатным направлениям { y, z};
– пространственная протяженность квантовой точки соответственно по координатным направлениям { y, z}; 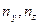 – квантовые числа из набора целочисленных величин {1, 2, …, ∞}, характеризующие локальное состояние микрочастицы соответственно по координатным направлениям { y, z}; kx – проекция волнового вектора поступательной формы движения электрона по направлению оси {x}.
– квантовые числа из набора целочисленных величин {1, 2, …, ∞}, характеризующие локальное состояние микрочастицы соответственно по координатным направлениям { y, z}; kx – проекция волнового вектора поступательной формы движения электрона по направлению оси {x}.
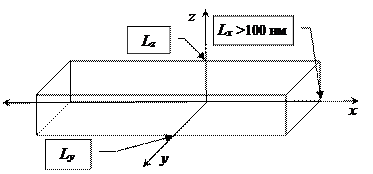
Рис. 1.18. Пространственное отображение квантовой проволоки
с характеристическими размерными параметрами { 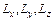 }
}
(Lx – микро-, мезо- или макроскопическая величина)
Из выражений (1.81) следует, что координатные составляющие допустимых значений энергии электронов, находящихся в пределах квантовой проволоки, могут принимать при движении электронов:
· по осям { y, z} – только ряд дискретных значений, разделенных друг от друга конечными интервалами энергии (как это уже имело место для случая квантовой точки);
· по оси {x} – практически непрерывный ряд значений (ввиду значительной протяженности наноразмерной структуры по данному направлению) в интервале величин { 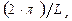 –
– 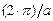 }, где a – параметр кристаллической структуры в направлении оси {x}.
}, где a – параметр кристаллической структуры в направлении оси {x}.
На рис. 1.19 представлено схематическое отображение энергетических спектров электронов в квантовой проволоке.


Рис.1.19. Схематическое отображение фрагмента
энергетической диаграммы состояния электронов в квантовой проволоке
Для пояснения энергетической диаграммы рис. 1.19 уместно привести следующие комментарии:
· все энергетические зависимости параболического типа приведены для случая фиксированного значения квантового числа nz;
· пунктирные прямоугольники характеризуют плоскости, в которых сохраняется постоянное значение координатного квантового числа ny, пробегающего от плоскости к плоскости ряд значений в диапазоне чисел (1, 2, 3);
· смещение индивидуальных параболических зависимостей вверх, наблюдаемое с ростом координатного квантового числа ny, обусловлено постоянным вкладом (при одновременных вариациях значения волнового вектора kx в диапазоне значений { 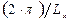 –
– 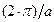 }) в энергию микрочастицы от фрагмента [
}) в энергию микрочастицы от фрагмента [ 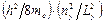 ] формулы (1.81);
] формулы (1.81);
· различие в начертании приведенных параболических зависимостей использовано с целью облегчения зрительного восприятия изображения.
Из сравнительного анализа рис. 1.16 и 1.19 следует то обстоятельство, что в наноразмерных структурах типа квантовой проволоки имеет место частичный отход от эффекта полной дискретизации энергии электронов, как это имело место в наноразмерных структурах типа квантовой точки.
Энергетический спектр (1.81) можно представить как функциональную зависимость от волновых векторов {kx, ky, kz}(процедура подобного перехода аргументов представлена выше, при рассмотрении структур типа (0D)):
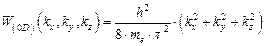 , ,
| (1.82) |
где волновые векторы {ky, kz} могут принимать строго фиксированные численные значения, соответствующие квантовым числам { 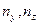 }, а волновой вектор {kx} – непрерывный ряд значений в диапазоне величин {
}, а волновой вектор {kx} – непрерывный ряд значений в диапазоне величин { 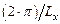 –
– 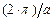 }, где a – параметр кристаллической решетки по координатному направлению {x}.
}, где a – параметр кристаллической решетки по координатному направлению {x}.
Применительно к наноразмерным системам типа (1D) функция плотности квантовых состояний электронов 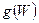 в направлениях, связанных с проявлением квантовых ограничений, имеет вид [5]
в направлениях, связанных с проявлением квантовых ограничений, имеет вид [5]
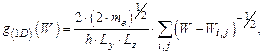
| (1.83) |
где индексы 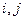 – пробегают ряд дискретных значений в диапазоне величин {1, 2,…, ∞}.
– пробегают ряд дискретных значений в диапазоне величин {1, 2,…, ∞}.
На рис. 1.20 представлено схематическое отображение фрагмента функции плотности квантовых состояний электронов 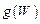 , находящихся в геометрических пределах наноразмерных структур типа (1D).
, находящихся в геометрических пределах наноразмерных структур типа (1D).
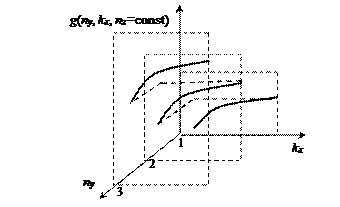

Рис. 1.20. Схематическое отображение фрагмента функции
плотности квантовых состояний электронов 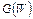 для структуры типа (1D)
для структуры типа (1D)
Для пояснения энергетической диаграммы рис. 1.20 уместно привести следующие комментарии:
· все три фрагмента функции 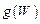 (сплошные толстые линии) приведены для случая фиксированного значения квантового числа nz;
(сплошные толстые линии) приведены для случая фиксированного значения квантового числа nz;
· пунктирные прямоугольники характеризуют плоскости, в которых сохраняется постоянное значение координатного квантового числа ny, пробегающего от плоскости к плоскости ряд значений в диапазоне чисел (1, 2, 3);
· смещение индивидуальных параболических зависимостей вверх, наблюдаемое с ростом координатного квантового числа ny, обусловлено постоянным вкладом (при одновременных вариациях значения волнового вектора kx в диапазоне значений { 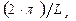 –
– 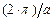 }) в энергию микрочастицы от фрагмента [
}) в энергию микрочастицы от фрагмента [ 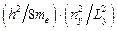 ] формулы (1.81);
] формулы (1.81);
· пунктирными линиями условно отображен фактор перехода от совокупности энергетических состояний, характеризуемых квантовым числом, от ny = j до состояний ny = j+1.
Приведенное на рис. 1.20 отображение функции 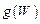 соответствует случаю отсутствия вырождения энергетических состояний, поскольку при построении графика принято, что квантовое число nz = const. В противном случае может иметь место пересечение индивидуальных фрагментов зависимости функции
соответствует случаю отсутствия вырождения энергетических состояний, поскольку при построении графика принято, что квантовое число nz = const. В противном случае может иметь место пересечение индивидуальных фрагментов зависимости функции 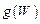 , что приведет к появлению фактора вырождения энергетических состояний электронов.
, что приведет к появлению фактора вырождения энергетических состояний электронов.
Совокупность электронов в квантовых проволоках принято называть одномерным электронным газом.
е) Спектр энергетических состояний в наноразмерных структурах
типа (2D)
В наноразмерных структурах типа (2D) движение электронов ограничено по одному координатному направлению. Это ограничение соответствует случаю нахождения микрочастицы в трехмерном потенциальном ящике, который имеет весьма малую протяженность по двум координатным осям {y, z} (рис 1.21). В современной научно-технической практике диапазон этой протяженности так же, как и было уже отмечено выше, сопоставим с интервалом значений характеристических длин порядка 1 – 100 нм. Именно исходя из этого обстоятельства такие структуры получили название квантовой пленки. Квантовые пленки, как и квантовые точки и проволоки, могут содержать в своем составе достаточно большое (в пределе бесконечное, при бесконечной протяженности пленки по координатным направлениям {x,y}) количество атомов.
Беря за основу одномерную модель потенциального ящика для координатного направления {z} (см. выражение (1.55)) и модельное представление о движении свободного электрона по координатным направлениям {x, y} (см. выражение (1.15)), для функции 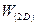 применительно к квантовой пленке имеем (сравнить приводимое ниже выражение с формулой (1.81))
применительно к квантовой пленке имеем (сравнить приводимое ниже выражение с формулой (1.81))
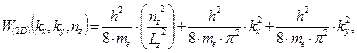
| (1.84) |
где me – эффективная масса электрона при его поступательной форме движения по координатному направлению {x}; 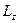 – пространственная протяженность квантовой пленки по координатному направлению с ограничением на фактор движения электрона { z};
– пространственная протяженность квантовой пленки по координатному направлению с ограничением на фактор движения электрона { z}; 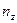 – квантовое число из набора целочисленных величин {1, 2,…, ∞}, характеризующих локальное энергетическое состояние электрона, по координатному направлению {z}; kx, ky – проекции волнового вектора поступательной формы движения электрона по координатным направлениям {x,y}.
– квантовое число из набора целочисленных величин {1, 2,…, ∞}, характеризующих локальное энергетическое состояние электрона, по координатному направлению {z}; kx, ky – проекции волнового вектора поступательной формы движения электрона по координатным направлениям {x,y}.

Рис. 1.21. Пространственное отображение квантовой пленки
с характеристическими размерными параметрами { 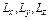 }
}
(Lx, Ly, Lz – микро-, мезо- или макроскопическая величина)
Энергетический спектр (1.84) можно представить как функциональную зависимость от волновых векторов {kx, ky, kz} (процедура подобного перехода аргументов представлена выше, при рассмотрении структур типа (0D) и (1D)):
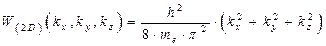 , ,
| (1.85) |
где волновой вектор {kz} может принимать строго фиксированные численные значения, соответствующие квантовому числу { 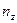 }, а волновые вектора {kx,ky} – соответственно непрерывный ряд значений в диапазоне величин
}, а волновые вектора {kx,ky} – соответственно непрерывный ряд значений в диапазоне величин
{ 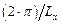 –
– 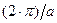 } и {
} и { 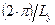 –
– 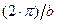 },
},
где a и b – параметры кристаллической решетки соответственно по координатным направлениям {x, y}.
На рис. 1.22 представлено схематическое отображение характерных моментов (фрагментов) энергетических спектров электронов, находящихся в пределах квантовой пленки.

Рис.1.22. Схематическое отображение фрагмента энергетической диаграммы
состояния электронов в квантовой пленке
Применительно к наноразмерным системам типа (2D) функция плотности квантовых состояний электронов 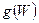 в направлениях, связанных с проявлением квантовых ограничений, имеет вид [5]
в направлениях, связанных с проявлением квантовых ограничений, имеет вид [5]
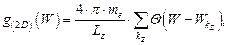
| (1.86) |
где kz – индекс, пробегающий ряд дискретных значений при изменении квантового числа nz  в диапазоне величин {1, 2, …, ∞};
в диапазоне величин {1, 2, …, ∞}; 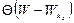 – условное обозначение ступенчато (kz) – непрерывной (kx, ky) функции специальной формы.
– условное обозначение ступенчато (kz) – непрерывной (kx, ky) функции специальной формы.
На рис. 1.23 представлено схематическое отображение характерных фрагментов функции плотности квантовых состояний электронов 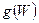 , находящихся в геометрических пределах наноразмерных структур типа (2D).
, находящихся в геометрических пределах наноразмерных структур типа (2D).
Рис. 1.23. Схематическое отображение фрагмента функции
плотности квантовых состояний электронов 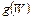 для структуры типа (2D)
для структуры типа (2D)
Из рис. 1.23 видно, что в кристаллических структурах типа (2D) может иметь место появление запрещенной зоны на энергетической диаграмме состояния электронов, если размеры квантовой пленки и по пространственным направлениям {x,y} будут в определенной мере ограничены (в этом случае следует обратить внимание на фрагменты 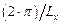 и
и 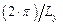 ).
).
Ввиду отмеченного выше, своеобразия энергетических диаграмм совокупность электронов в квантовых пленках в ряде случаев принято в научно-технической практике называть двумерным электронным газом.
Квантовые пленки уже в настоящее время нашли достаточно широкое практическое применение при создании широкого круга гетеропереходов на основе полупроводниковых и диэлектрических материалов, используемых в элементах конструкций микроэлектронных устройств.
Дата добавления: 2016-01-03; просмотров: 1351;
