Фазовая и групповая скорость. Дисперсия скорости

Как было указано в п. 1.2, в упругой среде малые возмущения распространяются со скоростью звука, являющейся фазовой скоростью. Для случая монохроматических плоских волн можно показать, что фазовая скорость гармонической волны есть

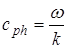. (1.18)

Так как возмущение (в нашем случае – гармоническое колебание) подчиняется волновому уравнению, то и в соотношении (1.18) частота и волновое число не могут быть произвольными. В случае линейных сред для малых возмущений в рамках волнового уравнения (1.2) .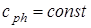

Рассмотрим далее некоторые вопросы, связанные с дисперсией. Напомним, что дисперсией называется функциональная зависимость 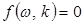между частотой 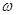и волновыми числом 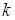, и в большинстве случаев она имеет явный вид

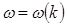. (1.19)

Если фазовая скорость постоянна или закон дисперсии (1.19) носит линейный характер, то такая среда называется бездисперсионной. Бездисперсионные среды обладают очень важным свойством: возмущение (1.4) распространяется в данной среде без изменения формы. Сказанное относится в полной мере и к гармоническим колебаниям (1.5). Так, если в некоторый момент времени возмущение имеет вид группы гармонических волн, то и в любой другой момент времени это возмущение будет иметь тот же вид, т. к. отдельные волны не изменят своего положения друг относительно друга.

В случае дисперсионной среды ситуация меняется. Любое возмущение (не обязательно периодическое) может быть представлено в форме ряда Фурье или Фурье-образа, т. е. в среде будет распространяться группа гармонических волн с различными волновыми числами. Теперь уже различные гармоники будут распространяться с различной фазовой скоростью, что приведет к изменению формы начального возмущения. Кроме того, для сред с дисперсией понятие скорости волны становится более сложным и требует дополнительных определений. Производная от правой части дисперсионного соотношения (1.18)

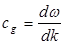(1.20)

имеет размерность скорости и называется групповой скоростью.

Реальные дисперсионные соотношения можно получить, подставляя функцию (1.4) в волновое уравнение. Таким образом может быть получено дисперсионное соотношение для гармонической волны в линейном приближении:

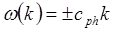. (1.21)

Нетрудно показать, что в общем случае одномерных процессов групповая скорость связана с фазовой скоростью следующим соотношением:

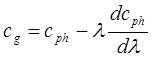. (1.22)

Выберем некоторое значение 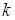и соответствующее ему значение 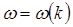как исходные величины и допустим, что к волновому числу 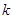добавляется малое возмущение 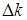. Соответствующее возмущенное значение частоты может быть аппроксимировано двумя членами ряда Тейлора:

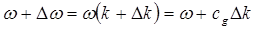, (1.23)

где 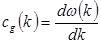. Тогда фаза 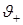, соответствующая этому возмущенному значению волнового числа, определяется выражением

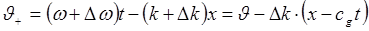, (1.24)

где 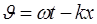невозмущенная фаза.

Если теперь 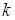не возрастает, а уменьшается до значения 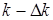, то соответствующая фаза определяется выражением

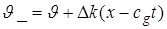. (1.25)

Решение волнового уравнения, соответствующее волновому числу 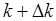, имеет вид

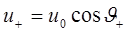. (1.26)

Решение 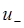записывается в виде 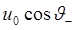с такой же амплитудой, как и 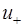. Суперпозиция двух решений дает

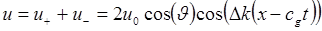. (1.27)

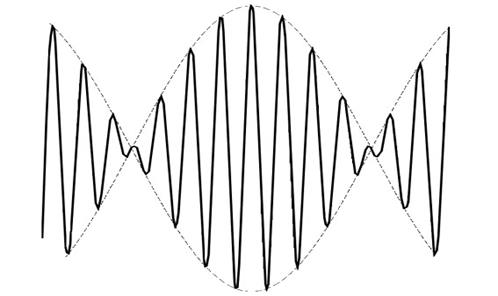
Графически это решение при 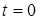изображено на рис. 1.1. Его можно рассматривать как волну с исходным волновым числом и частотой, модулированную по амплитуде множителем 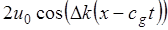. Другими словами, имеют место биения, соответствующие медленным изменениям амплитуды. Колебания ограничены двумя кривыми

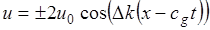. (1.28)

x u

Рис. 1.1. Решение с биениями (пунктиром обозначена огибающая колебаний)

Каждый участок огибающей (1.28) длиной 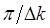можно интерпретировать как группу (пакет) волн, а скорость 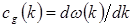– как скорость этой группы. Физический смысл групповой скорости заключается в том, что она равна скорости переноса энергии в направлении распространения волны.

Из сказанного следует, что в линейных средах групповая 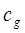и фазовая 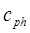скорости совпадают, однако это справедливо только при малых амплитудах смещения. Следует заметить, что учет дисперсии в упругих средах сопряжен с некоторыми сложностями, которые усугубляются, если имеет место диссипация энергии. Таким образом, имеем:

1) для сред без дисперси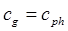и или ;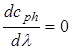

2) для сред с аномальной дисперсие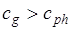й или ;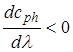

3) для сред с нормальной дисперсие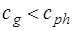й или .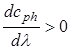

1.7. Энергетические характеристики упругих волн.
Вектор Умова-Пойнтинга

Акустические колебания являются упругими, поэтому все, что будет сказано об упругих колебаниях, справедливо и для акустических. Выделим малый объем среды и определим, как меняется со временем энергия, находящаяся в этом объеме среды. Акустическая энергияскладывается из кинетической энергии движения частиц среды и потенциальной энергии деформации.

Кинетическая энергия единицы объема есть

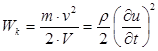. (1.29)

Потенциальная энергия единицы объема, связанная с упругой деформацией среды равна

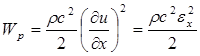. (1.30)

Принимая во внимание, что упругие колебания в плоском случае описываются уравнением (1.2), имеющим общее решение вида (1.3), при непосредственном дифференцировании выражения (1.3) получим

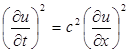, (1.31)

откуда, с учетом (1.29) и (1.30), следует, что .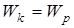

Это свидетельствует о том, что в малом объеме упругой среды кинетическая энергия равна потенциальной. Изменение их значений в волновом процессе происходит синфазно, т.е. в одинаковой фазе. Именно в этом заключается принципиальное отличие волнового процесса от простого колебательного движения, где кинетическая и потенциальная энергия изменяются в противофазе.

Распространение колебаний в упругой среде может представлено как распространение следующих типов волн:

- волны упругих деформаций (перенос потенциальной энергии);

- волны колебательных скоростей (перенос кинетической энергии).

Энергия единицы объема – это объемная плотность энергии, она равна

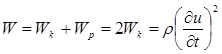. (1.32)

Для гармонических волн 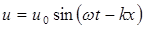, откуда имеем

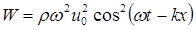. (1.33)

Таким образом, механическая энергия единицы объема пропорциональна плотности среды, квадрату амплитуды смещений и квадрату частоты колебаний. Объемная плотность энергии – величина переменная. Она различна в каждый момент времени и в каждой точке. Средняя за период плотность энергии гармонической волны в каждой точке волнового поля:

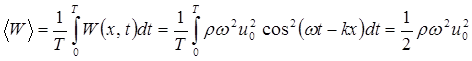. (1.34)

Объемная плотность энергии – локальная энергетическая характеристика. Перейдем к интегральным характеристикам. Энергия некоторого объема :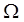

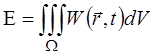. (1.35)

Поток или изменение энергии 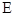по закону сохранения энергии равно:

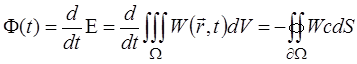. (1.36)

Это скалярная величина, которая не отражает направления переноса энергии. Для характеристики направления потока энергии в данной точке акустического поля вводят векторную величину – плотность потока энергии:

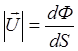. (1.37)

Величину 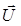называют вектором Умова-Пойнтинга. Его направление совпадает с направлением распространения волны:

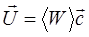. (1.38)

Интенсивность акустических волн – отношение потока акустической энергии сквозь поверхность, перпендикулярную направлению распространения, к площади этой поверхности. Таким образом, интенсивность (сила звука) равна модулю вектора Умова-Пойнтинга:

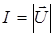. (1.39)

Основываясь на формулах (1.34), (1.38) и (1.39), можно сказать, что интенсивность звука – это средняя плотность энергии, переносимой через единичную площадку в направлении распространения волны.

В этом случае интенсивность одномерной гармонической волны равна

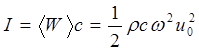. (1.40)

Из выражения (1.40) следует, что интенсивность упругой волны пропорциональна квадратам амплитуды и частоты колебаний и произведению плотности среды на скорость распространения волны, т.е. акустическому импедансу среды.

Учитывая, что звуковое давление 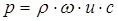, запишем:

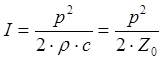(1.41)

Таким образом, интенсивность упругой волны определяется отношением квадрата амплитуды акустического давления к удвоенному акустическому сопротивлению среды. Полученная формула одинаково справедлива для плоских и сферических бегущих волн. Если не учитывать поглощение энергии ультразвука средой, то в случае плоских волн интенсивность не меняется с расстоянием. Однако для сферических волн интенсивность убывает обратно пропорционально квадрату расстояния (см. раздел 1.3).

Для стоячих волн интенсивность утрачивает смысл: I = 0, т.к. потока энергии в этом случае нет. Энергетической характеристикой таких волн является просто плотность акустической энергии.