Векторные формулы скорости и ускорения точек тела, вращающегося вокруг неподвижной оси.

Скорость любой точки тела, вращающегося вокруг неподвижной оси, может быть записана в виде

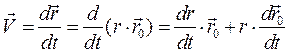(2.10)

Здесь 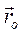- орт вектора 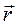, причём 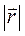=const, для определённости ось вращения обозначим OZ. Так как 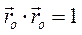, то 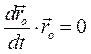, откуда следует, что первое слагаемое в формуле (2.10) равно нулю, а второе – перпендикулярно радиусу-вектору 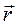. Тогда выражение для скорости можно записать в следующем ви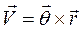де , где 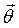- является вектором, который и надо определить. Раскроем векторное произведение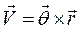

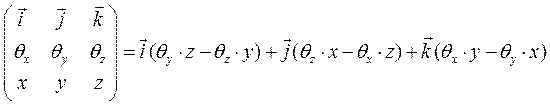(2.11)

Последнее слагаемое равно нулю, т.к. проекция скорости точки на ось вращения (на ось OZ) равна нулю (по определению), следовательно, для любых x и y должно выполняться 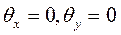и 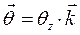, то-есть вектор 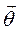направлен по оси вращения. Для точки, движущейся по окружности радиуса, уравнения движения записываются в виде

,

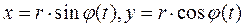а для скоростей точек получим выражение

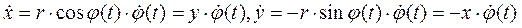. (2.12)

Из сравнения формул (2.11) и (2.12) следует, что 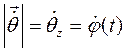. Вектор 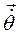, направленный по оси вращения и численно равный скорости изменения угла поворота, назовём вектором угловой скорости, в дальнейшем будем его обозначать 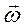. Тогда получим основную формулу кинематики твёрдого тела и, как увидим далее, она сохраняет свой вид и в случае вращения тела вокруг неподвижной точки (формула Эйлера)

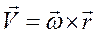(2.13)

Скорость конца вектор-радиуса постоянного по модулю определяется угловой скоростью вращения этого вектора. Величина векторного произведения (33) равна (рис.26) .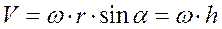

Вектор 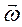можно расположить в любом месте на оси вращения, следовательно, это скользящий вектор в отличии от вектора скорости, который является приложенным вектором. Перейдём к рассмотрению ускорений точек тела вращающегося вокруг неподвижной оси. По определению ускорение точки есть производная от вектора скорости

,

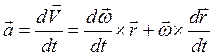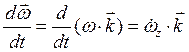
т.к. орт 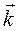не меняет своего направления, и, учитывая что 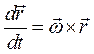, получим

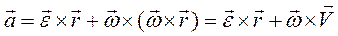(2.14)

Первое слагаемое 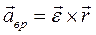- вращательное ускорение, направленное по вектору скорости при ускоренном вращении и против вектора скорости при замедленном вращении, модуль вращательного ускорения равен 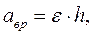второе слагаемое 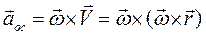- есть осестремительное ускорение, направленное всегда к оси вращения и численно равно 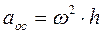(рис.26).

Глава 6.