Мгновенный центр скоростей плоской фигуры.
В предыдущем параграфе формула распределения скоростей в плоском движении была получена из представления о перемещении точки плоской фигуры в виде геометрической суммы перемещения полюса и перемещения поворота вокруг полюса. Докажем следующую теорему: при всяком непоступательном движении плоской фигуры существует точка фигуры, скорость которой в данный момент равна нулю.Точка Р плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей фигуры(сокращённо МЦС). Пусть скорость точки Р равна нулю 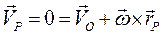 . Умножим написанное выражение векторно слева на вектор
. Умножим написанное выражение векторно слева на вектор 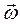 . Получим
. Получим 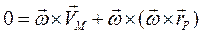 , раскрывая двойное векторное произведение, имеем
, раскрывая двойное векторное произведение, имеем
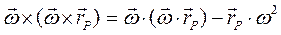 .
.
Первое слагаемое рано нулю, так как 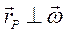 ,тогда получим
,тогда получим

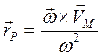 (2.18)
(2.18)
Модуль вектора 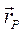 равен
равен 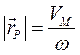 , а его направление перпендикулярно скорости
, а его направление перпендикулярно скорости 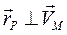 , так что скорости точек плоской фигуры можно рассматривать как враща-
, так что скорости точек плоской фигуры можно рассматривать как враща-
Рис. 31 тельные скорости их вокруг мгновенного центра скоростей, а сам мгновенный центр — как мгновенный центр вращения плоской фигуры. Отсюда можно сделать следующий общий вывод: поле скоростей в фигуре, совершающей плоское движение, в каждый момент таково, как будто фигура вращается вокруг неподвижного мгновенного центра, скорость любой точки плоской фигуры пропорциональна расстоянию до МЦС.При этом скорость любой точки плоской фигуры перпендикулярна к вектор-радиусу, соединяющему эту точку с мгновенным центром, и направлена в сторону вращения фигуры, а по величине пропорциональна расстоянию точки до мгновенного центра (рис. 31). В отличие от рассмотренного ранее случая вращения твердого тела вокруг неподвижной оси, где ось вращения была жестко связана с вращающимся телом и сохраняла одно и то же положение в неподвижном пространстве, относительно которого вращение происходило, в плоском движении мгновенный центр в каждый новый момент времени занимает другое положение как в движущейся фигуре, так и в неподвижной плоскости.
При движении плоской фигуры в ее плоскости мгновенный центр перемещается от одной точки фигуры к другой. Точно так же и в неподвижной плоскости мгновенный центр занимает все новые и новые положения. Траектория мгновенного центра в плоскости, связанной с движущейся фигурой, образует кривую, называемую подвижной центроидой; точно так же траектория мгновенного центра в неподвижной плоскости называется неподвижной центроидой. Так, при катания без скольжения круглого колеса по прямолинейному рельсу все точки контура колеса при различных положениях его будут служить мгновенными центрами скоростей, следовательно, окружность является подвижной центроидой. Точки рельса будут служить мгновенными центрами в неподвижной плоскости и представлять неподвижную центроиду. Подвижная и неподвижная центроиды имеют в каждый момент времени общую точку — мгновенный центр, траекториями которого они служат. При движении плоской фигуры в своей плоскости, подвижная центроида катится без скольжения по неподвижной.
 Рассмотрим пример. Пусть задана скорость точки А и угол α, а также направление скорости точки В. Длина отрезка АВ= а. Надо найти скорость точки и угловую скорость вращения плоской фигуры. Так как проекции скоростей концов отрезка на направление отрезка равны, то
Рассмотрим пример. Пусть задана скорость точки А и угол α, а также направление скорости точки В. Длина отрезка АВ= а. Надо найти скорость точки и угловую скорость вращения плоской фигуры. Так как проекции скоростей концов отрезка на направление отрезка равны, то 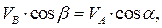 откуда получаем
откуда получаем
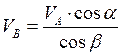 . (2.19) Из рис 32 видно, что
. (2.19) Из рис 32 видно, что 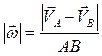 или
или 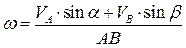 . Этот же результат можно получить с помощью МЦС. Мгновенный центр скоростей должен находиться на пересечении перпендикуляров к скоростям
. Этот же результат можно получить с помощью МЦС. Мгновенный центр скоростей должен находиться на пересечении перпендикуляров к скоростям 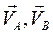 в точке Р. Из треугольника АВР следует, что
в точке Р. Из треугольника АВР следует, что 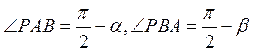 . Тогда по теореме синусов
. Тогда по теореме синусов 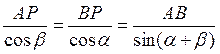 .
.
Но 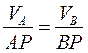 , откуда
, откуда 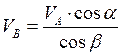 . Получаем формулу (2.19). Из теоремы синусов
. Получаем формулу (2.19). Из теоремы синусов 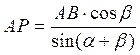 и угловая скорость равна
и угловая скорость равна 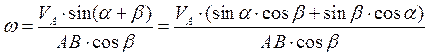 , после сокращений и используя (2.19) получаем
, после сокращений и используя (2.19) получаем
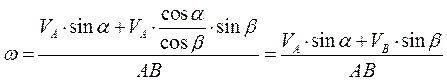
то же самое выражение, что и раньше.
Дата добавления: 2016-01-07; просмотров: 1547;
