Уравнения плоского движения.
 В предыдущей главе были рассмотрены два наиболее простых случая движения твердого тела: поступательное и вращательное вокруг неподвижной оси. Перейдем теперь к изучению более сложного случая движения – плоского - параллельного движения твердого тела, или (сокращённо) плоского движения. Под плоским движением понимают движение, при котором все точки твердого тела, расположенные в плоскостях, параллельных некоторой неподвижной плоскости, во все время движения остаются в тех же плоскостях. Если разбить мысленно тело на плоские сечения, параллельные заданной плоскости, то эти сечения будут скользить каждое в своей плоскости. Этот случай движения имеет большое техническое значение; механизмы, встречающиеся в технике, за немногочисленными исключениями, представляют системы твердых тел, совершающих плоское движение. Вращение тела вокруг неподвижной оси является частным случаем плос
В предыдущей главе были рассмотрены два наиболее простых случая движения твердого тела: поступательное и вращательное вокруг неподвижной оси. Перейдем теперь к изучению более сложного случая движения – плоского - параллельного движения твердого тела, или (сокращённо) плоского движения. Под плоским движением понимают движение, при котором все точки твердого тела, расположенные в плоскостях, параллельных некоторой неподвижной плоскости, во все время движения остаются в тех же плоскостях. Если разбить мысленно тело на плоские сечения, параллельные заданной плоскости, то эти сечения будут скользить каждое в своей плоскости. Этот случай движения имеет большое техническое значение; механизмы, встречающиеся в технике, за немногочисленными исключениями, представляют системы твердых тел, совершающих плоское движение. Вращение тела вокруг неподвижной оси является частным случаем плос
…Рис. 28 кого движения; движение колеса по прямолинейному пути дает еще один пример; плоское движение совершают также механизмы для вычерчивания разных кривых (эллипсограф, конхоидограф), всевозможные кулисные механизмы, эпициклические механизмы, применяемые в редукторах скоро  стей, и т. д. Пусть тело А (рис. 28) совершает движение, параллельное плоскости П. Проведем мысленно в теле ряд плоскостей П', II", ... , параллельных П. Тело разобьется на ряд плоских фигур S', S",… . Движение одной такой плоской фигуры вполне определяет движение всего твердого тела, так как плоскости, которыми мы разбили твердое тело, друг с другом не
стей, и т. д. Пусть тело А (рис. 28) совершает движение, параллельное плоскости П. Проведем мысленно в теле ряд плоскостей П', II", ... , параллельных П. Тело разобьется на ряд плоских фигур S', S",… . Движение одной такой плоской фигуры вполне определяет движение всего твердого тела, так как плоскости, которыми мы разбили твердое тело, друг с другом не
Рис 29 изменно связаны и не могут двигаться друг по отношению к другу. Если мы возьмем в какой-нибудь фигуре S' точку М и восставим в ней перпендикуляр к плоскости фигуры S, то точки М и М" фигур S' и S", лежащие на этом перпендикуляре, будут иметь одинаковое движение, т. е. будут описывать одинаковые траектории, иметь одинаковые скорости, одинаковые ускорения. Таким образом, можно значительно упростить изучение плоскою движения твердого тела — достаточно изучить движение одной плоской фигуры в ее плоскости. Следует здесь отметить, что при плоском движении тела все перемещения, скорости и ускорения точек должны лежать в плоскости фигуры. Возьмем две системы осей в плоскости движения фигуры: одну систему Оху неподвижную, другую - О'х'у', неизменно связанную с движущейся фигурой (рис. 29). Положение точки М фигуры в неподвижной плоскости будем определять вектор-радиусом 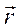 , проведенным из начала О неподвижной системы осей; выбор рассматриваемой точки фигуры определяется указанием вектора
, проведенным из начала О неподвижной системы осей; выбор рассматриваемой точки фигуры определяется указанием вектора 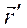 ', проведеного из начала О' подвижной системы. Вектор-радиус начала О' относительно О обозначим через
', проведеного из начала О' подвижной системы. Вектор-радиус начала О' относительно О обозначим через 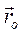 . Тогда
. Тогда
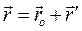
Проекции вектора 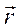 (t) на оси х и у могут быть записаны в виде
(t) на оси х и у могут быть записаны в виде
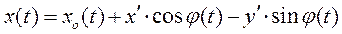
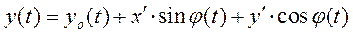 (2.15)
(2.15)
Декартовы координаты х' и 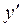 точки М в системе подвижных осей остаются постоянными.
точки М в системе подвижных осей остаются постоянными.
Дата добавления: 2016-01-07; просмотров: 1375;
