Упругие колебания в твердых средах. Скорость распространения волн в упругой среде

Как было сказано выше, движение газов и жидкостей, в том числе колебания, описываются давлением 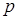, плотностью 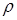и скоростью частиц среды v. При этом считается, что термодинамические свойства среды известны.

Нестационарные системы уравнений, описывающие динамику твердого деформируемого тела, могут иметь разную форму. В отличие от газовой динамики, выбор той или иной модели может существенно изменить структуру и свойства уравнений [6]. Кроме того, давление в твердых телах имеет иную природу, чем в газах или жидкостях [3], поэтому для описания динамики твердого тела оперируют уже деформациями и напряжениями.

В твердых телах следует выделять продольные и поперечные колебания. Уравнения малых упругих колебаний в неограниченной изотропной среде для плоской продольной и плоской поперечной волн имеют вид

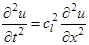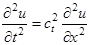и , (1.14)

где введены обозначения

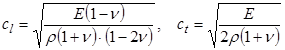. (1.15)

Видно, что уравнения (1.14) эквивалентны волновому уравнению (1.2), поэтому сразу можно сказать, что продольные волны распространяются со скоростью 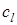, а поперечные – со скоростью 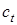. Так как в случае малых колебаний величины, входящие в (1.15), подвержены малым изменениям, то в акустическом приближени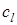и и 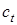– это постоянные для данного вещества величины. Кроме того, всегда выполняется неравенство 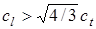[8]. Для большинства металлов .

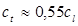Учитывая, что модуль сдвига 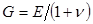, где Е – модуль Юнга, n –коэффициент Пуассона, выражения для продольной и поперечной скорости звука можно переписать в виде:

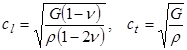. (1.16)

Для случая тонких стержней выражение для 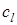имеет более простой вид:

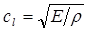. (1.17)

Так как в жидкостях и газах G → 0, то и c_t → 0. Это свидетельствует о том, что в жидкостях и газах распространяются только продольные волны.

Деформации сжатия и растяжения распространяются в упругой среде с одинаковыми скоростями, постоянными для данной среды (для твердых, жидких, газообразных сред). Однако это справедливо для малых деформаций. При конечных деформациях, высокоскоростных и высокоэнергетических процессах (удар, взрыв и т. д.) скорость звука уже не является постоянной величиной, и имеет смысл говорить о локальной скорости звука. Кроме того, при таких воздействиях сами возмущения также могут распространяться со сверхзвуковой скоростью, в этом случае возникают ударные волны.