Акустические колебания в газах и жидкостях
Состояние движущегося газа с известными термодинамическими свойствами определяется заданием скорости 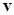 , плотности
, плотности 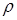 и давления
и давления 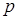 как функций координат и времени [3]. Для нахождения этих функций служит система уравнений, которая выводится из законов сохранения (непрерывности), движения и термодинамики. Достаточно подробно этот вопрос освящен в [7]. Отметим, что уравнения, входящие в данную систему – нелинейные, и в общем виде эта система не решается. В акустическом приближении, когда все возмущения среды считаются малыми, эта система, после некоторых манипуляций, редуцируется к ряду независимых уравнений второго порядка. Уравнение, описывающее изменение скорости движения газа относительно некоторой начальной (колебательной) скорости, имеет вид:
как функций координат и времени [3]. Для нахождения этих функций служит система уравнений, которая выводится из законов сохранения (непрерывности), движения и термодинамики. Достаточно подробно этот вопрос освящен в [7]. Отметим, что уравнения, входящие в данную систему – нелинейные, и в общем виде эта система не решается. В акустическом приближении, когда все возмущения среды считаются малыми, эта система, после некоторых манипуляций, редуцируется к ряду независимых уравнений второго порядка. Уравнение, описывающее изменение скорости движения газа относительно некоторой начальной (колебательной) скорости, имеет вид:
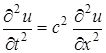 . (1.10)
. (1.10)
Уравнения, описывающие изменения давления и плотности, имеют аналогичный вид. При подробном выводе уравнения (1.10) можно получить, что
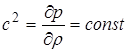 . (1.11)
. (1.11)
Это так называемая адиабатическая производная. Она равна квадрату скорости распространения малого возмущения, т.е. скорости звука. Используя уравнение (1.11) и уравнение состояния идеального газа, получаем
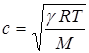 , (1.12)
, (1.12)
где 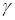 – показатель адиабаты;
– показатель адиабаты;
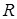 – универсальная газовая постоянная;
– универсальная газовая постоянная;
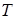 – абсолютная температура;
– абсолютная температура;
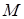 – молярная масса.
– молярная масса.
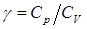 (1.13)
(1.13)
Показатель адиабаты является константой газовой среды, определяемой через удельные теплоемкости при постоянном давлении 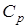 и постоянном объеме
и постоянном объеме 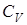 .
.
Дата добавления: 2015-12-10; просмотров: 2583;
