РАВНОВЕСИЕ ПЛАВАЮЩИХ ТЕЛ

Возьмем твердое тело АВ, погруженное в жидкость (рис. 2-29). Разобьем его на ряд вертикальных цилиндров с площадью поперечного сечения dS. Рассматривая один такой цилиндр, видим, что сверху на него давит вес столба жидкости, равный γh₂dS; снизу - вес столба жидкости, равный γh₁dS. Ясно, что рассматриваемый цилиндр твердого тела будет испытывать подъемное усилие (направленное вверх), равное:

dP_υ = (h₂ – h₁)γdS. (2-115)

Сумма элементарных подъемных сил dP_υ, действующих на все цилиндры, составляющие данное твердое тело, даст нам полную подъемную силу P_υ, стремящуюся поднять тело вверх.

Как видно, вертикальная подъемная сила P_υ (архимедова сила) равна весу жидкости в объеме рассматриваемого тела; точкой приложения силы P_υ является центр тяжести D объема жидкости АВ. Точка D называется центром водоизмещения. В общем случае точка D не совпадает с центром тяжести С твердого тела, где приложен его собственный вес G.

Рис. 2-29. Вертикальная подъемная сила P_υ (архимедова сила), G - вес твердого тела, С - центр тяжести его, D - центр водоизмещения

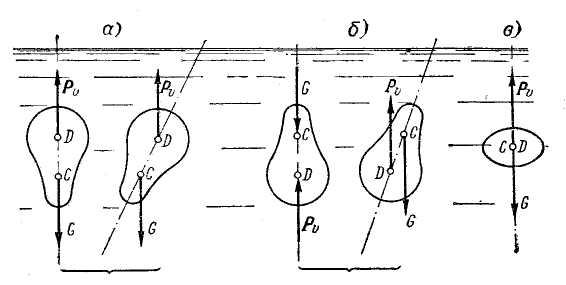
Рис. 2-30. Плавание тела в полностью погруженном состоянии

Можно различать следующие три случая:

P_υ 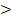G- тело тонет;

P_υ 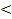G - тело всплывает на поверхность жидкости;

P_υ = G - тело плавает в погруженном состоянии.

1. Случай P_υ = G. Здесь, в свою очередь, можем различать (рис. 2-30):

а) устойчивое равновесие тела (схема а);

б) неустойчивое равновесие тела (схема б);

в) безразличное равновесие (схема в).

2. Случай P_υ 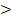G. В этом случае тело будет всплывать до тех пор, пока часть его не выйдет из жидкости (рис. 2-31, а), причем будет соблюдено условие

G = P’_υ, (2-116)

где P’_υ - вес жидкости, вытесненной плавающим телом.

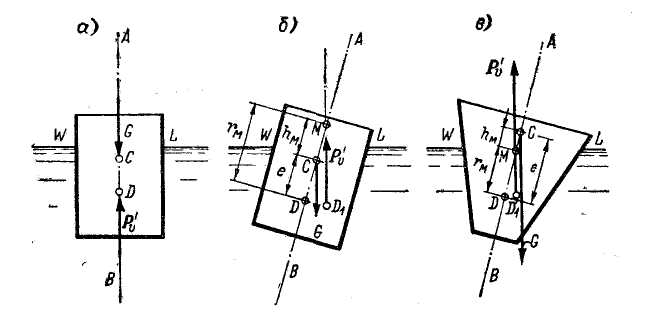
Рис. 2-31. Плавание судна в частично погруженном состоянии: а - состояние равновесия; б - остойчивое; в - неостойчивое С - центр тяжести судна, D - центр водоизмещения при отсутствии крена, D₁ - то же при наличии крена, М - метацентр, r_м - метацентрический радиус, h_м - метацентрическая высота, е - эксцентриситет

Рассмотрим схему, когда точка С (центр тяжести плавающего тела) выше точки D (центра водоизмещения). В этом случае, в отличие от схемы в на рис. 2-30, можем получить как неустойчивое, так и устойчивое равновесие. Поясним этот вопрос применительно к плаванию судна (в покоящейся воде), причем будем пользоваться следующими терминами и обозначениями (рис. 2-31):

WL - площадь грузовой ватерлинии (площадь горизонтального сечения судна по линии WL);

АВ - ось плавания;

С - центр тяжести судна;

D - центр водоизмещения при равновесии судна;

D₁ - центр водоизмещения при крене судна;

М - точка пересечения оси плавания АВ с вертикалью, проведенной через центр водоизмещения D₁; эта точка называется метацентром.

Сопоставляя два разных судна, представленных на рис. 2-31, б, в, видим следующее:

а) на схеме б центр водоизмещения D₁ при крене оказался правее точки С, причем возник момент, возвращающий судно в положение покоя. Данный случай характеризуется тем, что метацентр М лежит выше точки С;

б) на схеме в центр водоизмещения D₁ при крене оказался левее точки С, причем возник момент, опрокидывающий судно. Данный случай характеризуется тем, что метацентр М лежит ниже точки С.

Обозначим длины отрезков DC, СМ и DM соответственно через е, h_м и r_м;

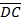= e; = h_M; 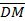= r_M = e + h_M. (2-117)

Эти отрезки называются: е - эксцентриситетом; h_м - метацентрической высотой; r_м - метацентрическим радиусом. Величина h_м считается положительной, если точка М располагается выше точки С (рис. 2-31,6), и отрицательной, если точка М располагается ниже точки С (рис. 2-31, в).

Остойчивостью судна называется способность его возвращаться в состояние равновесия после получения крена. Имея в виду сказанное, можем утверждать следующее:

1) если для данного судна h_м>0, или, что то же, r_м> е, то это судно является остойчивым (2-31, б);

2) если для данного судна h_м<0, или, что то же, r_м< е, то такое судно является неостойчивым (рис. 2-31, в).

Для данного судна эксцентриситет е является постоянной величиной.

При небольшом угле крена (меньше, например, 15°) можно считать, что точка D₁ перемещается по дуге окружности, описанной из метацентра радиусом r_м, причем сама точка М не меняет своего положения на оси плавания.

Как видно, для данного судна метацентрический радиус r_м и метацентрическая высота h_м считаются постоянными (в случае небольших кренов).

Можно показать, что метацентрический радиус

r_M = , (2-118)

где V - объем воды, вытесненной судном (объемное водоизмещение судна); I - момент инерции площади грузовой ватерлинии (рис. 2-31, а) относительно горизонтальной продольной оси, проходящей через центр тяжести этой площади.

Ясно, что чем больше для данного судна величина r_м (сравнительно с величиной е), тем больше остойчивость судна.