ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПОКОЯ (РАВНОВЕСИЯ) ЖИДКОСТИ

Умножаем 1-е дифференциальное уравнение (2-14) на dx, 2-е на dy и 3-е на dz. После этого складываем левые и правые части этих уравнений:

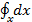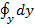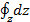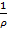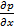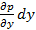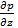+ + - ( dx+ + dz) = 0. (2-15)

Так как давление в точке р есть функция только координат:

p = ƒ(x, y, z), (2-16)

то можно утверждать, что выражение, входящее в равенство (2-15) и заключенное в скобки, является полным дифференциалом р, т. е. это выражение равно dp. Поэтому уравнение (2-15) можно переписать в виде

dp = 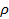( 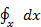+ + 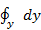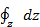). (2-17)

Далее рассуждаем следующим образом.

Если левая часть (2-17) является полным дифференциалом некоторой функции, зависящей от координат, то, следовательно, и правая часть (2-17) должна являться полным дифференциалом некоторой функции, зависящей от координат. Учитывая, что плотность жидкости ρ=const, можно на основании сказанного утверждать, что выражение, входящее в (2-17) и заключенное в скобки, является также полным дифференциалом некоторой функции, зависящей от координат. Обозначим эту последнюю функцию через U, причем U = ƒ(x, y, z). Тогда вместо (2-17) можем написать

dp = ρdU, (2-18)

где

dU = 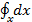+ + 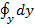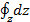(2-19)

С другой стороны, полный дифференциал dU можно представить как сумму частных дифференциалов:

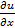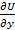dU= dx+ dy+ 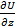dz. (2-20)

Сопоставляя (2-19) и (2-20), видим, что

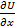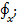
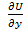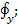
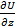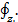= = = (2-21)

Так как U есть функция только координат и так как частные производные ее по координатам дают соответствующие проекции ( 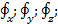) объемной силы, отнесенной к единице массы, то, следовательно, U является потенциальной функцией. Объемная же сила 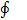, удовлетворяющая условиям (2-21), является силой, имеющей потенциал. Из сказанного ясно, что однородная несжимаемая жидкость (для которой ρ=const) может находиться в покое под действием только таких сил, которые имеют потенциал. Интегрируя (2-18), получаем

p = ρU + C, (2-22)

где С - постоянная интегрирования.

Чтобы определить С, рассматриваем некоторую точку жидкости, для которой известны р и U:

p = p_0; U=U₀. (2-23)

Для этой точки (2-22) перепишется в виде

p₀=ρU₀ + C, (2-24)

откуда

C = p₀ – ρU₀. (2-25)

Подставляя (2-25) в (2-22), получаем

p = ρU + p₀ – ρU₀ (2-26)

или окончательно

p= p₀ + ρ(U – U₀).. (2-27)

Формула (2-27) дает давление в точке для случая, когда ρ=const, причем на жидкость действует любая система объемных сил, имеющих потенциал.

Понятие потенциальной функции. Пространство, в котором происходит какое-либо физическое явление, называется физическим полем.

Различают поля: 1) скалярные, например поле температур; 2) векторные, например поле сил или поле скоростей.

Поле какого-либо скаляра

Ψ = ƒ(x, y,z)

может быть представлено линиями (или поверхностями) ψ=const; например, поле температур t^o можно представить линиями (или поверхностями) t^o=const . Оперировать векторным полем значительно сложнее, чем скалярным, Поэтому векторное поле (например, поле сил) при его изучении заменяют особым скалярным полем. При этом такое скалярное поле представляют линиями равного значения особой функции U, называемой потенциальной функцией, или просто потенциалом (потенциалом тех векторов, поле которых мы изучаем; можно различать потенциал сил, потенциал скоростей и т. п.). U является скалярной величиной.

Функция U (потенциал) обладает следующими свойствами:

а) она зависит только от координат х, у, z (и иногда от времени);

б) частные производные U по координатам, взятые в различных точках скалярного поля, должны давать величины проекций рассматриваемых векторов в соответствующих точках векторного поля.

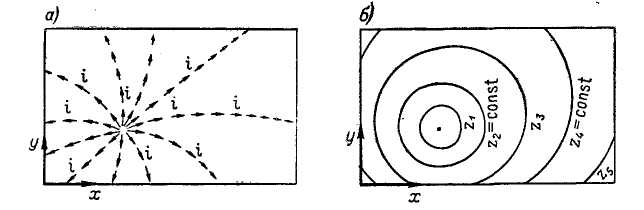
Рис. 2-6. Замена векторного поля (а) уклонов i земной поверхности скалярным полем (б) отметок земной поверхности

Рассмотрим для примера рельеф поверхности земли. В каждой точке этого рельефа имеется некоторый уклон земной поверхности, который можно представить вектором, направленным вдоль линии наибольшего ската. В связи с этим рельеф поверхности земли можно рассматривать как поле уклонов i (поле векторов, выражающих уклоны; рис. 2-6, а).

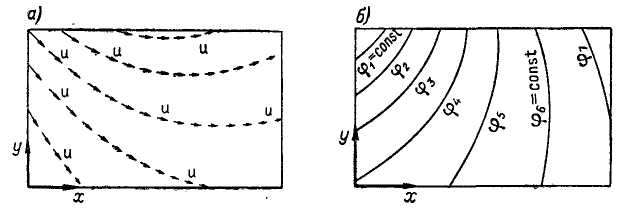
Рис. 2-7. Векторное поле (а) скоростей и скалярное поле (б) потенциальной функции 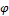поля скоростей

Обозначим теперь через z отметку поверхности земли и проведем на плане нашего рельефа горизонтали, т. е. линии (рис. 2-6, б). Очевидно, отметка z зависит только от координат х и у; кроме того величина z обладает еще следующим свойством:

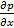= - i_x; 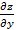= - i_y

где i_x и i_y - компоненты i.

Отсюда ясно, что скалярная величина z является потенциальной функцией векторного поля уклонов i. Хорошо известно, что в практике рельеф местности всегда представляют именно эквипотенциалами z=const, причем из рассмотрения этих линий (горизонталей) легко можно установить значение и направление вектора i в любой точке земной поверхности.

Выше, имея векторное поле объемных сил 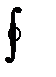(отнесенных к единице массы), мы ввели в рассмотрение скаляр U (потенциал векторного поля объемных сил).

Далее нам часто придется сталкиваться с векторным полем скоростей и (рис. 2-7, а). В этих случаях мы будем иногда заменять такое поле скалярным полем, характеризующимся потенциалом скорости 𝜑 (рис. 2-7, б).

Подчеркнем, что не каждое векторное поле может быть представлено (описано) потенциальной функцией. Имеются такие векторные поля, которые не имеют потенциала. Изучение таких полей в значительной мере затрудняется. При рассмотрении векторных полей, имеющих потенциальную функцию, сталкиваемся с особой математической задачей об отыскании этой функции (см. с. 80).