СВОЙСТВА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ

ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ.

СИЛА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ

СУММАРНОЕ ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ»).

СВОЙСТВА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ

В гидростатике изучается жидкость, находящаяся в покое. В § 1-2 было отмечено, что касательные напряжения в покоящейся жидкости всегда равны нулю (τ=0). В § 1-4 п. 3 мы исключили возможность существования в жидкости (покоящейся или движущейся) растягивающих напряжений. Поэтому, мы должны считать, рассматривая покоящуюся жидкость, что в любой ее точке мы можем иметь только нормальные напряжения: σ=σ_n

(см. конец § 1-6).

Основным понятием гидростатики является понятие гидростатического давления в данной точке покоящейся жидкости. Это давление принято обозначать буквой р и для краткости именовать просто «гидростатическим давлением».

В случае покоящейся жидкости гидростатическим давлением р в данной точке называют скалярную величину, равную модулю (значению) напряжения σ в рассматриваемой точке:

p= δ, (2-1)

где | σ| - модуль напряжения σ (независящий от ориентировки - от угла наклона - площадки действия, намечаемой в рассматриваемой точке; см. рис. 1-10, б, относящийся к случаю, когда τ=0).¹ Имея это в виду, иногда говорят, что гидростатическое давление в данной точке представляет собой «шаровой тензор»; при этом несколько условно отмечают, что в случае гидростатики любая точка (т. е. элементарная частица жидкости) со всех сторон «сжата одинаково» (что обычно не имеет места в случае гидродинамики; см. далее § 3-1).

Поясним еще гидростатическое давление р следующим образом.

Представим на рис. 2-1 произвольный объем покоящейся жидкости. Наметим внутри этого объема точку М и проведем через нее произвольную поверхность АВ. Такая поверхность рассечет данный объем жидкости на два отсека: I и II. Выделим у точки М на поверхности АВ некоторую площадь S.

Через поверхность АВ будет передаваться сила давления со стороны отсека I на отсек II. Часть этой силы, обозначаемая нами через Р, должна приходиться на выделенную площадь S.

Сила Р, действующая на всю рассматриваемую площадь S, называется силой гидростатического давления (или суммарным гидростатическим давлением).

Сила Р по отношению к отсеку II является внешней поверхностной силой; по отношению же ко всему объему жидкости, состоящему из двух отсеков (I и II), она является силой внутренней. Силе Р отвечает реакция (той же величины, что и сила Р), действующая со стороны отсека II на отсек I. Поэтому силу Р следует рассматривать, как силу парную.

Разделив модуль (значение) | Р| на S, получим

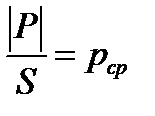, (2-2)

где величина p_ср представляет значение той силы, которая приходится в среднем на единицу рассматриваемой площади S; p_ср называют средним гидростатическим давлением.

Если теперь представить, что в формуле (2-2) площадь S стремится к нулю (так, однако, чтобы точка М всегда находилась внутри контура площадки S, стягиваемого в точку), то величина p_ср будет стремиться к определенному пределу. Этот предел выражает модуль (значение) напряжения σ, а следовательно, и значение р в намеченной точке М:

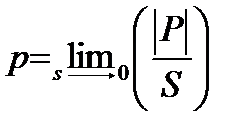(2-3)

Из (2-2) и (2-3) видно, что величины p_ср и р имеют размерность силы, деленной на площадь (например, кН/м², тс/м², кгс/см² и т. п.).

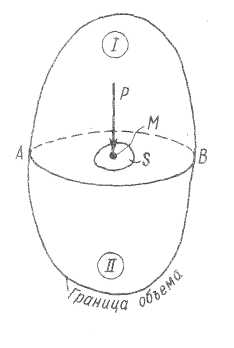
Рис. 2-1. Объем покоящейся жидкости Р — сила, действующая со стороны I отсека жидкости на площадку S, принадлежащую II отсеку

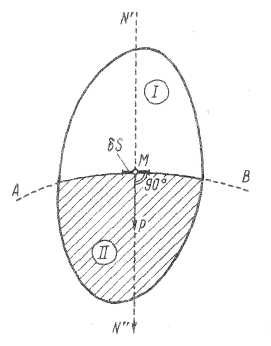
Рис. 2-2. Гидростатическое давление р (см. точку М) MN" - внутренняя нормаль

Из всего сказанного выше можно видеть, что гидростатическое напряжение σ и гидростатическое давление р обладают двумя свойствами:

1. Первое свойство. Напряжение σ, модулем которого является р, действует нормально к площадке действия и является сжимающим, т. е. оно направлено внутрь того объема жидкости (или твердого тела, ограничивающего жидкость), который мы рассматриваем.

На рис. 2-2 представлен некоторый объем жидкости, находящийся в покое, рассеченный поверхностью АВ на два отсека I и II. Как отмечалось выше, отсек I будет с некоторой силой давить на поверхность АВ отсека II; с такой же силой, но обратной по направлению, отсек II будет давить на поверхность АВ отсека I.

Условимся далее рассматривать только отсек II, покрытый на чертеже штриховкой. При этом нам придется интересоваться первой названной силой, т. е. силой, приложенной к отсеку II (со стороны отсека I).

Наметим на поверхности АВ точку М и выделим у этой точки элементарную площадку действия δS, совпадающую с поверхностью АВ. Проведем к площадке δS нормаль N'N". Линии MN' и MN" принято называть нормалями, соответственно внешней и внутренней.

Как видно, согласно первому свойству, гидростатическое напряжение σ всегда направлено, как показано на рисунке, по нормали внутренней, т. е. внутрь того тела, давление на которое мы рассматриваем.

2. Второе свойство. Гидростатическое давление р в данной точке не зависит от ориентировки, т. е. от угла наклона площадки действия.

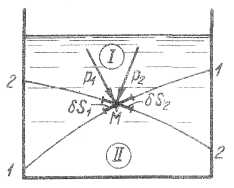
Рис. 2-3. Значение гидростатического давления в точке М (р₁=р₂)

На рис. 2-3 представлен объем покоящейся жидкости, заключенной, например, в сосуде. Наметим внутри жидкости произвольную точку М; через эту точку проведем несколько поверхностей (1-1, 2-2 и т.д.); как видно, каждая из этих поверхностей разбивает рассматриваемый объем жидкости на два отсека: I и II. Выделим далее у точки М ряд площадок действия (δS₁, δS₂ и т.д.), лежащих соответственно на поверхностях 1-1, 2-2 и т.д.; как видно, все эти площадки имеют различную ориентировку. Условимся теперь рассматривать давление, приходящееся со стороны отсека I на отсек II; при этом давление р в точке М для различных площадок действия (δS₁, δS₂ и т.д.) обозначим соответственно р₁, р₂ и т.д.

Согласно первому свойству, напряжение а в точке М должно быть нормально к соответствующим площадкам действия; согласно же второму свойству давление р (р₁, р₂, ...), т. е. длины векторов, показанных на рисунке, должны быть одинаковы:

p₁=p₂=p₃=… (2-4)

Как известно, для твердого тела в общем случае такое соотношение не имеет места.

§ 2-2. О НЕЗАВИСИМОСТИ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ р ОТ ОРИЕНТИРОВКИ ПЛОЩАДКИ, НАМЕЧЕННОЙ В ДАННОЙ ТОЧКЕ ПРОСТРАНСТВА (В УСЛОВИЯХ, КОГДА В ЖИДКОСТИ ОТСУТСТВУЮТ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ)

Как мы видели, второе свойство гидростатического давления (о независимости р от ориентировки площадки действия) вытекает из теории сплошной среды (см. рис. 1-10, б). Вместе с тем справедливость этого свойства может быть доказана непосредственно в результате нижеследующих рассуждений.

Возьмем внутри покоящейся жидкости произвольную точку А (рис. 2-4) и выделим у этой точки элементарный объем жидкости в виде прямой треугольной призмы ABC (на чертеже ABC - основание призмы, сама призма расположена перпендикулярно к чертежу).

Обозначим через а произвольный угол наклона грани ВС к горизонту. Наметив оси координат, как показано на чертеже, обозначим через dx, dz и dl длины сторон основания призмы; через dy - высоту призмы; все эти величины считаем бесконечно малыми.

Покажем теперь у точки А три элементарные площадки различной ориентировки: S_x, S_z, S_n; площадка S_n параллельна грани ВС; наклон ее к горизонту определится произвольным углом α. Давление в точке А для этих площадок соответственно будет: р_х, р_z, р_n. При этом среднее гидростатическое давление для граней АВ, АС и ВС должно быть записано в виде:

( p_x+ ε_x) - для грани АВ,

(p_z+ ε_z) - для грани АС,

(p_n+ ε_n) - для грани ВС,

где ε_x, ε_z, ε_n - величины бесконечно малые, которыми следует пренебрегать. Среднее давление, например, для грани АВ отличается от давления р_х в точке А на бесконечно малую величину потому, что величина р_х изменяется вдоль оси Az непрерывно; расстояние же dz бесконечно мало. Таким образом, можно утверждать, что величины р_х, р_z и р_n выражают также и средние гидростатические давления для соответствующих боковых граней призмы.

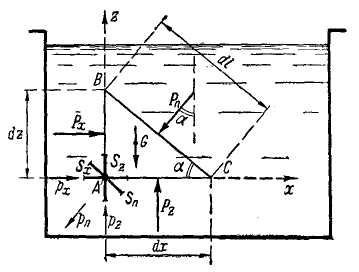
Рис. 2-4. Независимость значения величины р от ориентировки площадки S, намеченной в точке А

Выделенная призма ABC находится в равновесии под действием следующих сил:

1) сил P_x, P_y, P_z гидростатического давления со стороны окружающей жидкости, действующего на боковые грани призмы(нормально к ним), причем

P_x=p_xdzdy; P_y=p_ydxdz; P_n=p_ndldz; (2-5)

2) сил P_y гидростатического давления со стороны окружающей жидкости, действующего на торцовые грани ABC призмы; силы P_y нормальны к плоскости чертежа и на нем не показаны;

3) объемной внешней силы G; под силой G, в частности, можно подразумевать собственный вес выделенной призмы.

Объемная сила G будет величиной 3-го порядка малости, в то время как поверхностные силы Р будут величинами 2-го порядка малости. Действительно, для получения объемной силы G величину этой силы, отнесенную к единице объема (конечную величину), приходится умножать на объем призмы, т.е. на ( 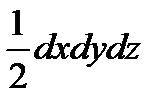); для получения же поверхностных сил средние гидростатические давления (конечные величины) мы умножали [см. (2-5)] на площади боковых граней, т. е. на (dz dy); (dx dy); (dl dy). Поэтому силой G следует пренебрегать и считать, что выделенная элементарная призма ABC находится в равновесии под действием только внешних поверхностных сил Р_х, P_z, Р_n, Р_у.

Имея это в виду, можем утверждать, что суммы проекций сил Р_х, P_z, Р_n и Р_у на оси Ах и Аz должны равняться нулю, т. е.

P_x-P_nsinα=0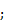

P_z-P_ncosα=0.

Подставляя в эти выражения зависимости (2-5), имеем

p_xdzdy-p_ndldysinα=0;

p_zdxdy-p_ndldycosα=0 (2-7)

Учитывая, что dlsinα=dz и dlcosα=dx, из (2-6) окончательно получаем:

p_n=p_x=p_z (2-7)

Таким образом, p_n оказывается равным p_x=p_z, какой бы угол α мы не задали.

Если теперь дополнительно учесть, что призму ABC (вместе со скрепленными с нею осями координат) можно как угодно располагать (ориентировать) в точке А, то справедливость высказанного выше свойства делается очевидной.

Таким образом, мы еще раз убеждаемся в том, что при отсутствии в рассматриваемом теле касательных напряжений величина (значение) давления (напряжения) в любой точке данного тела не зависит от ориентировки (от угла наклона) «площадки действия».