А) Зависимость момента от потока Ф и активной составляющей тока ротора .

Вращающий момент в асинхронной машине, как отмечалось, создается в результате взаимодействия вращающегося поля и токов, наведенных им в обмотке ротора. Его значение можно найти, исходя из закона электромагнитных сил.

На рис. 3-42 представлены кривые распределения индукции В и наведенных в обмотке ротора токов i₂по окружности ротора асинхронного двигателя, причем эти кривые приняты синусоидальными.

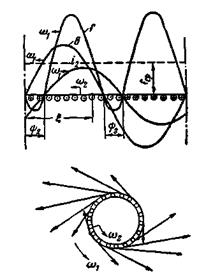
Рис. 3-42. Распределение индукции В, токов i₂ и тангенциальных сил f по окружности ротора.

При постоянных напряжении на зажимах статора и нагрузке на валу двигателя (s = const) обе кривые имеют неизменные амплитуды B_м и I_2м и остаются неподвижными одна относительно другой. Сдвиг между ними равен Ψ₂ (в электрических радианах) в соответствии со сдвигом по фазе э.д.с. и тока ротора.

Электромагнитная сила, действующая в тангенциальном направлении на проводник с током,

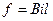. (3-107)

Возьмем проводник, сдвинутый на угол ξ (в электрических радианах) относительно нулевого значения индукции. Индукция в месте, где находится проводник, B = B_мsinξ; ток в этом проводнике 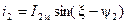. Следовательно,

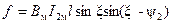. (3-108)

На рис. 3-42 (вверху) показана кривая распределения тангенциальных сил f на окружности ротора, найденная согласно (3-108). На этом же рисунке (внизу) показаны тангенциальные силы, приложенные к ротору.

Кривые В и i₂ относительно статора вращаются с синхронной частотой ω₁. С такой же частотой относительно статора вращается кривая f; относительно ротора она вращается с частотой sω₁.

Среднее значение тангенциальных сил f, необходимое для расчета момента, определяется следующим образом:

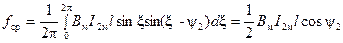. (3-109)

Общую силу F, действующую на ротор, найдем, умножив среднюю силу f_ср на число проводников N₂ обмотки ротора:

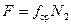. (3-110)

Вращающий момент равен произведению силы F на плечо 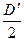, где D'—диаметр ротора:

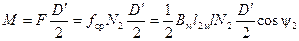. (3-111)

Учитывая, что

; ; ; ,

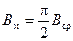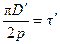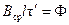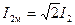получим, Дж:

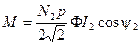. (3-112)

Формула (3-112) справедлива для обмотки ротора, выполненной в виде беличьей клетки. В общем случае для любой обмотки ротора необходимо учесть укорочение шага и распределение по окружности ротора катушек катушечной группы. Для этого нужно ввести в (3-112) обмоточный коэффициент k₀₂, тогда момент, Дж,

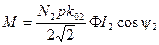(3-113)

или момент, кг.м,

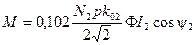. (3-114)

Если помножить (3-113) на ω₁, и при этом учесть, что

; ; ,

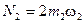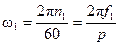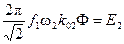то получим выражение для электромагнитной мощности:

.

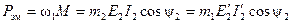Точно такое же выражение для Р_эм мы получили при помощи векторной диаграммы двигателя (§ 3-10).

Формула (3-113) показывает, что М зависит от величин Ф, I₂ и cos 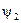, которые в свою очередь зависят от скольжения. Поэтому она не дает в явной форме зависимости М от скольжения или от частоты вращения. Однако вывод выражения (3-113) помогает уяснить физическую картину образования электромагнитного момента М.