А) Однофазная обмотка.

На рис. 3-22,а показаны статор и ротор двухполюсной асинхронной машины с воздушным зазором между ними. который всегда делается равномерным для асинхронных машин. На статоре в пазах помещена только одна катушка, имеющая ширину, равную полюсному делению. Если пропустить по катушке ток, то она создаст двухполюсное магнитное поле, индукционные линии которого показаны на рис. 3-22,а.

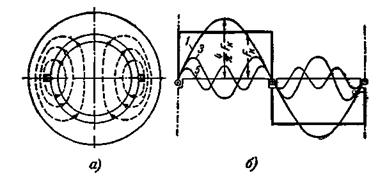
Рис. 3-22. Намагничивающая сила катушки.

Намагничивающая сила, действующая по замкнутому контуру, образованному любой индукционной линией, равна полному току, охваченному этим контуром. Следовательно, все н.с., действующие по пунктирным контурам, будут одинаковы.

Так как обе части машины симметричны относительно плоскости, проходящей через катушечные стороны, то на каждую половину магнитной цепи будет приходиться половина н.с. катушки и ее можно считать за н.с. приходящуюся на полюс.

Развернем внутреннюю окружность статора в прямую линию, как показано на рис. 3-22,б. Здесь жирная линия представляет собой кривую распределения н.с. вдоль окружности статора. Из сказанного следует, что н.с. распределена равномерно. Если пренебречь магнитным сопротивлением стальных участков, то под кривой н.с. можно понимать кривую распределения магнитного напряжения воздушного зазора. Такой же вид в этом случае будет иметь кривая распределения индукции в воздушном зазоре или кривая поля машины.

Если по катушке проходит переменный синусоидальный ток, то поле будет также переменным; оно будет пульсировать по оси катушки.

Намагничивающая сила катушки на полюс при максимальном значении тока 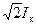равна:

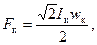(3-32)

где w_к — число витков катушки.

Можно указанную кривую н.с. заменить ее гармониками, из которых на рис. 3-22,б показаны первая, третья и пятая. Амплитуда первой (или основной) гармоники

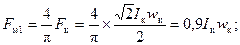(3-33)

амплитуда v-й гармоники

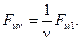(3-34)

Намагничивающая сила катушечной группы, состоящей из q катушек шириной t, вычисленная по первым гармоникам н.с. каждой катушки (рис. 3-23,б),

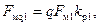(3-35)

где k₀₁ — коэффициент распределения, который рассчитывается, так же как для э.д.с., по (3-18), что следует из сопоставления рис. 3-23,б и рис. 3-9.

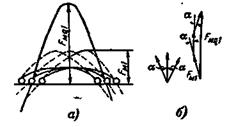
Рис. 3-23. Намагничивающие силы q катушек (а) и векторная сумма н.с. отдельных катушек (б).

Намагничивающая сила той же катушечной группы, но рассчитанная для ν-х гармоник н.с. катушек,

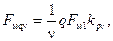(3-36)

где k_pv определяется по (3-28).

При двухслойных обмотках, которые выполняются обычно с укороченным шагом, необходимо при определении н.с. учесть укорочение шага. На рис. 3-24,а показана часть одной фазы двухслойной обмотки с укороченным шагом. Рассматривая токи верхнего и нижнего слоев, можно установить, что верхние и нижние слои как бы образуются из катушек шириной t (см. также рис. 3-15), причем эти катушки образуют группы, оси которых сдвинуты на угол 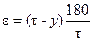эл. град.

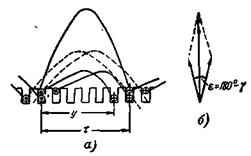
Рис. 3-24. Намагничивающая сила одной фазы двухслойной обмотки.

Следовательно, н.с. одной фазы двухслойной обмотки на один полюс равна:

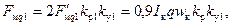(3-37)

где 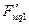— амплитуда н.с. "катушечной группы" верхнего или нижнего слоя;

w_к — удвоенное число витков катушки двухслойной обмотки;

k_у1 — коэффициент укорочения, который рассчитывается по (3-10), как и для э.д.с., что следует из рис. 3-24,б.

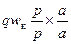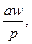Заменяя через где w — число последовательно соединенных витков фазы обмотки, и учитывая, что аI_к = I — ток этой фазы, получим:

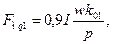(3-38)

где k₀₁=k_р1k_у1 обмоточный коэффициент для первой гармоники н.с.

Для амплитуды n-й гармоники н.с. мы можем написать:

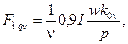(3-39)

где k_0ν — обмоточный коэффициент для ν-й гармоники н.с., который определяется, так же как для ν-й гармоники э.д.с., по (3-26) — (3-28).

Из табл. 3-1 можно видеть, что укорочение шага позволяет значительно снизить амплитуды высших гармоник в кривой н.с. При y = 0,83t наиболее заметно уменьшаются амплитуды пятой и седьмой гармоник, следующие по величине после третьей гармоники, а так как последняя пропадает в н.с. трехфазной обмотки (см. § 3-4,б), то обычно и выбирают указанное значение шага у. Пульсирующую по оси фазы н.с., синусоидально распределенную и имеющую при максимальном токе 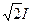амплитуду F_мq1, можно заменить двумя синусоидально распределенными н.с., но вращающимися в разные стороны с одинаковыми частотами и имеющими неизменные амплитуды 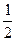F_мq1 что доказывается следующим образом.

Обратимся к рис. 3-25, где показана кривая пульсирующей н.с. с амплитудой F_t1 = F_мq1sinωt, соответствующей моменту t, когда ток в фазе равен 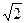Isinωt.

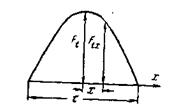
Рис. 3-25. Кривая пульсирующей н.с.

Значение н.с., соответствующей точке окружности статора, сдвинутой на x относительно оси фазы, будет:

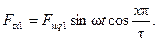(3-40)

Равенство (3-40) согласно известному уравнению

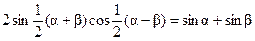
может быть записано в следующем виде:

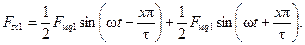(3-41)

Первое слагаемое правой части обозначим через F':

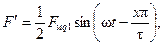(3-42)

Полученное уравнение называется уравнением бегущей волны. Оно показывает, что н.с. 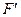является функцией времени t и места х. Если принять, что выражение в скобках равняется постоянной величине с (изменение t компенсируется изменением х), то мы найдем, с какой частотой будет перемещаться н.с. Действительно, дифференцируя уравнение 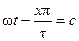по t, получим: 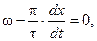а отсюда

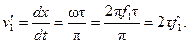(3-43)

С такой частотой будет перемещаться любое значение н.с., а следовательно, и ее амплитуда 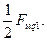Так как при вращательном движении перемещение на 2t соответствует 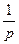части оборота, то частота вращения волны н.с. (ее первой гармоники),об/с,

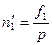
и ─ в об/мин,

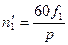. (3-44)

Обозначив второе слагаемое равенства (3-41) через F", мы также получим уравнение бегущей волны:

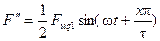. (3-45)

Однако частота ее перемещения и 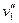, найденная аналогичным образом, будет отрицательной:

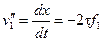, (3-46).

так же как и частота вращения, об/мин,

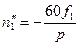. (3-47)

Это значит, что н.с. 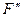перемещается в обратную сторону (положительному приращению dt соответствует отрицательное приращение dx).

Таким образом, мы получили две вращающиеся н.с., которые можно изобразить вращающимися пространственными векторам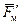и и 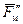(рис. 3-26).

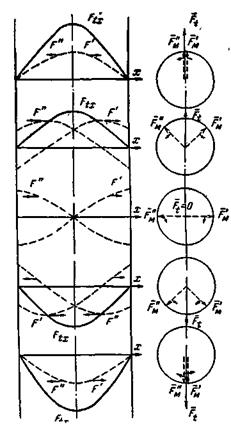
Рис. 3-26. Замена пульсирующей н.с. двумя круговыми вращающимися н.с.

Пространственным вектором заменяется синусоидально распределенная н.с. Его проекция на линию, проведенную через центр внутренней окружности статора и любую ее точку, определяет н.с., соответствующую этой точке.

Пространственный вектор 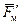или 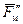при вращении опишет окружность, поэтому соответствующая н.с. называется круговой вращающейся н.с.

Определим значение 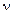-й гармоники н.с. для той же точки х (рис. 3-25). Оно равно:

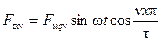, (3-48)

так как теперь тому же сдвигу х относительно оси фазы А будет соответствовать сдвиг 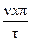в электрических радианах (полюсное деление для 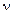-й гармоники равно t/ν). Заменим пульсирующую н.с. F_txν двумя вращающимися:

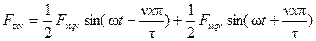. (3-49)

Рассуждая аналогично предыдущему, найдем, что одна из них перемещается со скоростью 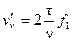или вращается с частотой

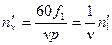, (3-50)

в ν раз меньшей частотой вращения первой гармоники. Вторая н.с. вращается в обратную сторону с той же частотой:

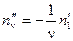. (3-51)