В) Волновая обмотка.

При волновой обмотке второй шаг y₂ делается в ту же сторону, что и первый шаг y₁ (рис. 5-11,б), поэтому шаги обмотки связаны соотношением

y₁ + y₂ = y = y_к. (5-7)

Результирующий шаг у должен быть больше или меньше, чем двойное полюсное деление 2t, чтобы при обходе секций все они были включены в обмотку. Поэтому, делая один обход по окружности якоря, мы попадаем в элементарный паз, сдвинутый вправо или влево от начала обхода на х делений элементарных пазов (рис. 5-11,б). Так как мы должны при этом сделать столько результирующих шагов у, сколько имеется пар полюсов, то yp±x = Z_э = S. Отсюда получаем:

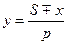(5-8)

Число параллельных ветвей волновой обмотки зависит только от х, оно равно 2а = 2х. В этом можно убедиться, рассматривая схемы обмоток.

Формула для результирующего шага пишется следующим образом

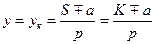. (5-9)

Верхний знак соответствует неперекрещенной обмотке, нижний знак — перекрещенной.

При а = 1 получается простая волновая обмотка или простая последовательная обмотка. При а > 1 получается сложная волновая или сложная последовательная обмотка.

На рис. 5-16 приведена схема-развертка простой волновой обмотки:

2p = 4; Z_э = S = K = 19; 2a = 2;

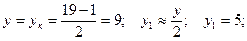
y₂ = y – y₁ = 4.

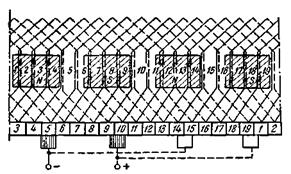
Рис. 5-16. Схема-развертка простой волновой обмотки
Z_э = S = K = 19; 2р = 4; у = y_к = 9; y₁ = 5; y₂ = 4; а = 1.

Радиальная схема той же обмотки приведена на рис. 5-16а.

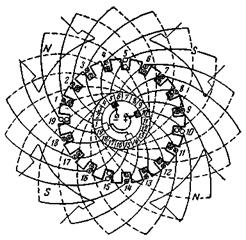
Рис. 5-16а. Радиальная схема простой волновой обмотки (кривые линии вне якоря условно показывают лобовые соединения на задней стороне машины, кривые внутри якоря — лобовые соединения на ее передней стороне (см рис. 5-16).

На рис. 5-17 представлены параллельные ветви обмотки, соответствующие положению якоря и коллектора относительно полюсов и щеток, показанному на рис. 5-16. Получаются две параллельные ветви. Для любой волновой обмотки можно взять только две щетки (заштрихованные на рис. 5-16 и 5-17). Однако в обычных случаях берут число щеток равным числу полюсов, так как в этом случае поверхность коллектора лучше используется и его размеры можно сократить. Выключаемые при этом секции (замкнутые щетками) практически не изменяют (при большом числе секций в параллельной ветви) ее э.д.с.

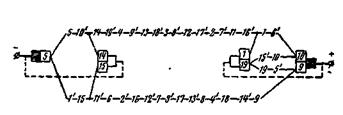
Рис. 5-17. Параллельные ветви простой волновой обмотки (см. рис. 5-16) при двух щетках и при четырех щетках.

Сложную волновую обмотку можно представить себе, как а простых волновых обмоток, уложенных на якоре, имеющем число пазов и число коллекторных пластин в а раз больше, чем это нужно для одной простой волновой обмотки. Сложные волновые обмотки на практике встречаются сравнительно редко.

Простая волновая обмотка находит себе самое широкое применение для нормальных машин небольшой и средней мощности при 2р=4 и 6. Ее преимущество перед простой петлевой обмоткой заключается в том, что она при любом числе полюсов имеет только две параллельные ветви и, следовательно, при 2р>2 требует меньше проводников. При этом сечение проводников должно быть взято больше, чем при петлевой обмотке, но при меньшем числе проводников изготовление обмотки облегчается. Другим важным преимуществом простой волновой обмотки является то, что она не требует уравнительных соединений, тогда как петлевая обмотка при 2р>2 должна быть снабжена уравнительными соединениями.

Число параллельных ветвей волновой обмотки, как отмечалось, зависит только от х коллекторных делений между началом и концом одного обхода по окружности коллектора. Это можно доказать, пользуясь теми же рассуждениями, что и в отношении петлевой обмотки. Для волновой обмотки можно также построить векторные диаграммы э.д.с. — многоугольники э.д.с. обмотки. Здесь сдвиг по фазе э.д.с. секций, следующих одна за другой при обходе обмотки, соответствует их сдвигу в магнитном поле, равному 2t-у (см. рис. 5-11,б). Так как число параллельных ветвей 2а равно общему сдвигу в магнитном поле при обходе всех секций обмотки, т. е. (2t-y)S, поделенному на t, то получим: 2а = (2t-y)S:t. Подставляя сюда (5-8) и t=S/2р, будем иметь:

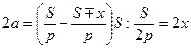(здесь знак минус опускаем, так как 2а — число существенно положительное).