Д) Равносекционные и ступенчатые обмотки.

При выполнении обмотки из проводников небольшого сечения, когда секция состоит из нескольких витков, следует так выбирать шаг y₁, чтобы все секции были одинаковыми по ширине. В этом случае секции могут быть объединены в катушки, хорошо изолированы вне машины и в готовом виде заложены в пазы якоря.

Обмотка с секциями, одинаковыми по ширине, называется равносекционной. Секции этой обмотки представлены на рис. 5-18. Здесь катушка состоит из трех секций; следовательно, она имеет по три конца с каждой стороны, которые присоединяются к коллекторным пластинам в соответствии с шагом по коллектору у_к. Таких катушек должно быть заготовлено столько, сколько пазов имеет якорь.

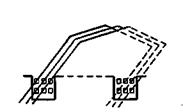
Рис. 5-18. Равносекционная обмотка.

Для равносекционной обмотки ширина секции (шаг у₁) выбирается таким образом, чтобы при положении одной ее стороны в верхнем слое одного паза, например в крайнем левом положении, другая сторона находилась в нижнем слое другого паза, также в крайнем левом положении (рис. 5-18). Следовательно, для равносекционной обмотки y₁/u должно быть равно целому числу (u — число секционных сторон в одном слое паза).

Если y₁/u не равно целому числу, то получается ступенчатая обмотка (рис. 5-19). Такая обмотка применяется при секциях, состоящих из одного витка. Обычно секции ступенчатой обмотки образуются из полусекций (стержней), закладываемых в пазы, путем соединения при помощи хомутиков их концов на стороне, противоположной коллектору. Она применяется для машин большой мощности, так как создает лучшие условия коммутации (см. § 5-7).

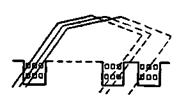
Рис. 5-19. Ступенчатая обмотка.

5-4. Электродвижущая сила

На рис. 5-20 представлена кривая поля машины при холостом ходе (или кривая распределения индукции В в воздушном зазоре вдоль окружности якоря). Допустим, что щетки стоят на геометрической нейтрали. Тогда можем считать, что при y₁ = t все проводники одной параллельной ветви обмотки находятся как бы под одним полюсом, так как в этом случае э.д.с. сторон витка складываются арифметически.

Электродвижущая сила, наводимая в проводнике, движущемся со скоростью v и имеющем активную длину l, равна:

e_x = B_xlv, (5-10)

где В_х— индукция в той точке, где в данный момент находится проводник.

Для определения э.д.с. параллельной ветви Е_a (э.д.с. якоря) нужно просуммировать э.д.с. всех N/2a проводников, составляющих параллельную ветвь (N — общее число проводников обмотки якоря):

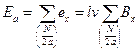. (5-11)

Сумму индукций в правой части формулы (5-11) с большой точностью можно заменить произведением средней индукции В_ср (рис. 5-20) и числа N/2a:

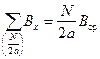. (5-12)

Подставляя в (5-11) 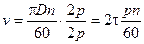и найденное значение суммы индукций, а также учитывая, что

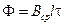, (5-13)

получим искомую формулу для э.д.с.:

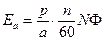, (5-14)

где Ф — магнитный поток, В·с.

Отметим, что под Ф в формуле (5-14) следует понимать магнитный поток, определяемый площадью фигуры, ограниченной кривой поля, осью абсцисс и линиями, проведенными через щетки (рис. 5-20). Если щетки сместить с геометрической нейтрали, то э.д.с. в параллельной ветви уменьшится в соответствии с уменьшением потока Ф, так как последний теперь будет определяться разностью площадей А и В (рис. 5-20).

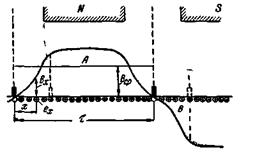
Рис. 5-20. Кривая поля и наведение э.д.с. в параллельной ветви обмотки якоря.

5-5. Магнитная цепь и ее расчет

На рис. 5-21 изображена магнитная цепь машины постоянного тока. Расчет ее заключается в определении н.с., необходимой для создания в воздушном зазоре машины магнитного потока, могущего навести в обмотке якоря заданную э.д.с.

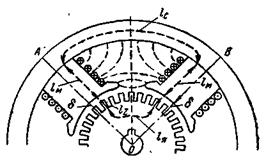
Рис. 5-21. Магнитная цепь машины постоянного тока.

Картина распределения магнитного поля в машине в пределах ее сектора АОВ (рис. 5-21) для всех подобных секторов одинакова. Поэтому для определения н.с., создающей магнитный поток, достаточно ограничиться расчетом магнитного поля в пределах одного сектора, т. е. в пределах одной пары полюсов. Обозначим искомую н.с. через F_цепи. Она, как указывалось, для замкнутого контура магнитной линии (показана жирным пунктиром на рис. 5-21) определяется равенством

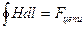, (5-15)

где Н — напряженность поля в направлении dl, правая часть равенства — полный ток внутри рассматриваемого контура, равный н.с.

Интеграл 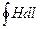заменяют суммой 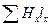и выбирают отдельные участки магнитной цепи таким образом, чтобы H₁, H₂, ... вдоль этих участков можно было считать приблизительно постоянными. При этом (5-15) переходит в

H₁l₁ + H₂l₂ + … + H_nl_n = F_цепи. (5-16)

Левая часть этого равенства представляет собой сумму магнитных напряжений. Перепишем ее в следующем виде:

F₁ + F₂ + … + F_n = F_цепи , (5-17)

где F_x = Н_xl_x, т. е. F_x равно магнитному напряжению какого-либо участка магнитной цепи (х = 1, 2,..., n).

Магнитную цепь машины разбиваем на следующие участки: 1) 2d — воздушные зазоры; 2) 2l_z — зубцы якоря; 3) l_a — сердечник якоря; 4) 2l_м — полюсы; 5) l_с — ярмо статора.

Расчет н.с. F_цепи, производим в таком порядке: по э.д.с. Е_а, которая должна наводиться в обмотке якоря, находим магнитный поток Ф [см. формулу (5-14)]; по размерам машины находим сечение S_x для каждого участка магнитной цепи; затем определяем индукцию

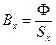; (5-18)

по значению B_x, пользуясь кривыми намагничивания для соответствующего материала, находим Н_х и Н_xl_x; наконец, просуммировав магнитные напряжения всех участков, определяем н.с. цепи F_цепи.

Магнитные напряжения для полюсов (и ярма статора) находятся по потоку Ф_м (и Ф_м/2), который больше потока Ф в воздушном зазоре из-за наличия поля рассеяния. Магнитные линии этого поля в промежутке между полюсами показаны на рис 5-21 тонким пунктиром.

Отношение Ф_м / Ф = s называется коэффициентом рассеяния полюсов.

Таким образом, имеем:

Ф_м = sФ; (5-19)

для нормальных машин постоянного тока

s = 1,12÷1,17.

Задаваясь различными значениями э.д.с. в пределах Е_а= (0,5 ÷ 1,25) U_н и определяя соответствующие значения потока Ф и затем, как указано, F_цепи, можем построить кривую Е_а = f(F_цепи).

На рис. 5-22 представлена кривая Е₀ = f(F_цепи), здесь э.д.с. Е_а обозначена через Е₀, чтобы показать, что мы имеем э.д.с. при холостом ходе машины. Приведенная кривая называется характеристикой холостого хода. Она имеет важное значение при исследовании электрической машины.

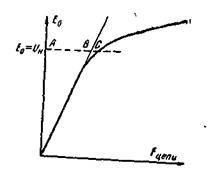
Рис. 5-22. Характеристика холостого хода.

На оси абсцисс можно было бы вместо F_цепи взять ток в обмотке возбуждения I_в, называемый током возбуждения. Он равен I_в = F_цепи /2w_в, где w_в — число витков обмотки возбуждения на одном полюсе.

Начальная часть характеристики идет в виде прямой линии, так как она соответствует ненасыщенному состоянию стальных участков магнитной цепи. Здесь можно считать н.с. F_цепи равной магнитному напряжению воздушных зазоров F_d, a F_d пропорциональна Ф или Е₀. При увеличении э.д.с. Е₀, а следовательно, и потока Ф начинает сказываться насыщение стальных участков магнитной цепи; характеристика холостого хода при этом искривляется.

При E₀ = U_н и при номинальной скорости вращения n_н большая часть F_цепи приходится на воздушные зазоры 2d. Для нормальных машин постоянного тока имеем приблизительно такое соотношение:

F_d / F_цепи = 0,80 ÷ 0,9. На рис. 5-22 это соотношение .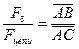

5-6. Реакция якоря

При холостом ходе машины магнитное поле в ней создается только обмоткой возбуждения, так как только по этой обмотке будет проходить ток. При нагрузке ток проходит и по обмотке якоря, н.с. которой изменяет поле машины, на что впервые была указано Э. X. Ленцем.

Воздействие н.с. якоря на поле машины называется реакцией якоря. При помощи рис. 5-23 мы можем выяснить, как изменяется поле машины в результате этого воздействия. На рис. 5-23,а изображено поле машины при ее холостом ходе, когда оно создается только н.с. обмотки возбуждения. На рис. 5-23,б показано поле якоря. Такое поле получается в машине при наличии тока только в обмотке якоря. При этом сам якорь превращается в электромагнит. Его н.с. имеет ось, всегда совпадающую с линией щеток.

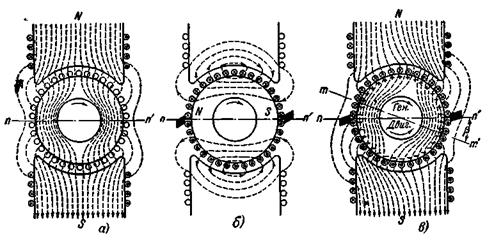
Рис. 5-23. Реакция якоря при положении щеток на геометрической нейтрали.
а — поле при холостом ходе; б — поле якоря, в — поле при нагрузке (nn' — геометрическая нейтраль, mm'—физическая нейтраль)

Мы расположили щетки на геометрической нейтрали, т. е. на линии, перпендикулярной оси полюсов. В этом случае токи в проводниках якоря верхней и нижней его частей имеют противоположные направления. Намагничивающая сила якоря, действующая по линии щеток, будет наибольшей, так как соответствующая магнитная линия охватывает наибольший полный ток. Далее н.с. убывает и под серединой полюса становится равной нулю. Можно приближенно считать, что она убывает по закону прямой линии, как это показано на рис. 5-24, где кривая 2 представляет собой кривую н.с. якоря, ординаты которой равны соответствующей н.с. якоря на половину обхода (на один полюс).

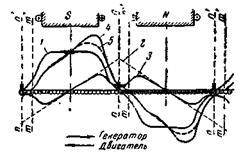
Рис. 5-24. Реакция якоря при положении щеток на геометрической нейтрали.
1 — кривая поля при холостом ходе, 2 — кривая н.с, якоря, 3 — кривая поля якоря, 4 — кривая результирующего поля без учета изменения насыщения, 5 — кривая действительного поля машины при нагрузке (nn' — геометрическая нейтраль, mm' —физическая нейтраль).

На рис. 5-23,е показано поле машины при ее нагрузке. Мы видим, что в результате реакции якоря поле машины, работающей генератором, изменилось: произошло усиление поля под сбегающей половиной полюса и ослабление его под набегающей половиной полюса. Другим следствием реакции якоря является смещение физической нейтрали, т. е. линии, проходящей через точки окружности якоря, где индукция равна нулю.

При холостом ходе физическая нейтраль совпадает с геометрической. При нагрузке она смещается относительно геометрической нейтрали: при работе генератором — в сторону вращения, при работе двигателем — против вращения (при принятых на рис. 5-23,в направлениях поля и токов в обмотке якоря машина при работе двигателем будет вращаться в обратную сторону).

На рис. 5-24 показаны кривые поля машины при холостом ходе и при нагрузке: здесь также приведена кривая поля якоря. Если кривую поля машины при ее нагрузке будем определять, исходя из принципа наложения, т. е. складывая ординаты кривой поля при холостом ходе 1 и кривой поля якоря 3, то получим кривую результирующего поля 4. Однако принцип наложения здесь не может дать точных результатов, так как поле в ферромагнитных телах не является линейной функцией тока. Кривая действительного поля машины при нагрузке 5 отличается от кривой результирующего поля 4. Кривая 5 показывает, что ослабление поля под набегающей половиной полюса будет больше, чем усиление поля под сбегающей половиной полюса (вследствие насыщения главным образом зубцов якоря). В результате получается ослабление общего поля и, следовательно, уменьшение полезного потока Ф, определяющего значение э.д.с. якоря.

Уменьшение э.д.с. якоря при положении щеток на геометрической нейтрали также вызвано смещением физической нейтрали, так как при этом и параллельные ветви будут входить проводники с обратными э.д.с. (см. рис. 5-23,в, где крестами и черточками внутри якоря показаны направления э.д.с., наведенных в проводниках).

В машинах мощностью от 0,3 кВт и выше обычно применяются дополнительные полюсы, о назначении которых сказано в следующем § 5-6. Они помещаются между главными полюсами (рис. 5-1), оси их совпадают с геометрическими нейтралями машины. Их обмотка соединяется последовательно с обмоткой якоря таким образом, чтобы ее н.с. действовала против н.с. обмотки якоря. Действие н.с. дополнительных полюсов ограничивается сравнительно неширокой зоной поверхности якоря, где находятся проводники замыкаемых щетками секций. Щетки при наличии дополнительных полюсов должны стоять на геометрической нейтрали.

В небольших машинах, не имеющих дополнительных полюсов, щетки нужно сдвинуть вслед за физической нейтралью: в генераторе — по вращению, в двигателе — против вращения.

В этом случае для определения влияния реакции якоря его н.с. F_a, действующую по линии щеток, заменяют двумя н.с. F_q и F_d, действующими по продольной и поперечной осям машины и в сумме равным F_a (рис. 5-25,а и б; на рис. 5-25,а стрелки показывают направления н.с.).

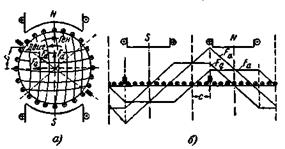
Рис. 5-25. Разложение н.с. якоря F_а на поперечную F_q и продольную F_d н.с.

Поперечная н.с. F_q реакции якоря практически действует так же, как н.с. якоря F_a при положении щеток на геометрической нейтрали, т. е. искажает поле под главными полюсами и несколько уменьшает полезный поток Ф (рис. 5-24).

Продольная н.с. F_d реакции якоря действует против н.с. обмотки возбуждения и, следовательно, уменьшает полезный поток Ф. При сдвиге щеток в обратную сторону от геометрической нейтрали мы получили бы продольную н. с. F_d, действующую согласно с н.с. обмотки возбуждения и, следовательно, увеличивающую полезный поток Ф. Однако такой сдвиг для нормальных машин недопустим, как будет показано в § 5-7, из-за возникающего при этом искрения под щетками.

Поперечная н.с. якоря, как мы видели искажает поле под главными полюсами и вместе с этим уменьшает полезный поток Ф, которым определяется э.д.с. якоря Е_а при данной скорости вращения. Мы можем пренебречь действием н.с. якоря вне полюсной дуги и считать, что поле под полюсами искажается вследствие действия н.с. якоря, равной на полюс b_dА; здесь b_d — длина полюсной дуги (обычно b_d » 0,68t [см]), А/см;

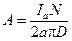, (5-20)

есть линейная нагрузка, условно показывающая нагрузку в амперах, приходящуюся на 1 см длины окружности якоря (I_а/2а — ток в проводнике обмотки).

Рассматриваемая н.с. b_dА действует по обходу, включающему воздушные зазоры, зубцы якоря, пути по ярму якоря и поперек полюса. Последними двумя магнитными сопротивлениями можно пренебречь и считать, что поперечная н.с. якоря изменяет лишь магнитные напряжения воздушных зазоров и зубцов. Поэтому используется "переходная" характеристика (рис. 5-26), представляющая собой зависимость

B_d = f [0,5(F_d + F_z)], (5-21)

где B_d = Ф/ b_d l_d — индукция в воздушном зазоре (расчетная длина по оси 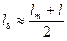, где l_m — длина полюса; l — длина якоря за вычетом радиальных вентиляционных каналов).

Под каждой половиной полюса действует н.с. якоря 0,5b_dA. Отложим 0,5b_dA вправо и влево от н.с., соответствующей индукции B_dE. Последняя определяется по э.д.с. якоря

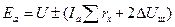. (5-22)

Здесь обозначают: U — напряжение на зажимах машины, I_a — ток якоря;Sr_x — сумму сопротивлений внутренней цепи якоря; 2DU_щ —падение напряжения в переходных контактах щеток, которое практически можно принять постоянным при изменении тока якоря в пределах 0,2—1,5 I_н и приближенно равным 2 В при угольных и графитных щетках. В формуле (5-22) нужно взять знак плюс для генератора, знак минус для двигателя.

Из рис 5-26 видим, что поток, который при холостом ходе можно принять пропорциональным площади прямоугольника ACHF, при нагрузке уменьшается, так как теперь он будет определяться площадью криволинейного четырехугольника ABGF. Уменьшение потока под одной половиной полюса будет больше, чем увеличение потока под другой половиной полюса. При этом мы принимаем, что при холостом ходе машины индукция в воздушном зазоре по длине дуги якоря b_d (практически равной длине дуги полюсного наконечника) распределена равномерно, а при нагрузке она распределена соответственно кривой BEG.

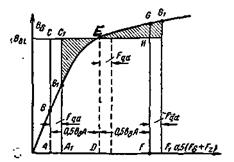
Рис. 5-26. Переходная характеристика (к определению размагничивающей н.с. F_qd обусловленной поперечной реакцией якоря).

Для того чтобы поток при нагрузке остался неизменным, необходимо н.с. обмотки возбуждения увеличить на некоторую величину F_qd, которая находится следующим образом.

Передвинем отрезок 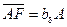вправо настолько, чтобы заштрихованные площади были равны между собой. При этом мы получаем площадь криволинейного четырехугольника A₁B₁G₁F₁ равной площади прямоугольника ACHF. Найденная указанным способом F_qd и представляет собою ту н.с., которую должна добавочно создать обмотка возбуждения, чтобы скомпенсировать размагничивающее действие поперечной н.с. якоря.

Значение нс. F_qd будет, очевидно, зависеть от насыщения машины, т. е. от положения точки Е на переходной характеристике, и от тока якоря I_а. Обе эти зависимости имеют сложный характер и не могут быть точно выражены аналитически. Если принять, что машина (как это обычно бывает) работает при насыщении, соответствующем точке E на переходной характеристике, то можно допустить, что при небольшом отклонении от этой точки, вызванном изменением Е_а из-за изменения внутреннего падения напряжения, н.с F_qd зависит только от I_a. Как показывают опыт и расчеты, для машин, у которых поперечная реакция якоря резко проявляется, зависимость F_qd от I_а может быть приближенно представлена следующим уравнением:

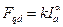, (5-23)

где k — постоянный коэффициент; a » 1,5 ÷ 2 для тока якоря I_а = (0,6 ÷ 1,5) I_н.

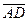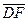Величина F_qd будет относительно тем больше, чем меньше воздушный зазор машины Действительно, при уменьшении воздушного зазора будет уменьшаться F_d и, следовательно, будет уменьшаться масштаб m_а (A/мм) для н.с. на оси абсцисс рис 5-26. Тогда отрезки и , равные 0,5b_dA/m_a [мм], будут увеличиваться, что приведет к возрастанию F_qd.

Для небольших машин (до 30 ÷ 40 кВт) иногда при I_а = I_н отрезок 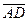получается несколько больше отрезка 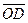. В этом случае под одним краем полюсного наконечника будет иметь место "опрокидывание" поля, т. е. изменение его направления. Для машин средней и большой мощности (примерно свыше 50 кВт) воздушный зазор обычно выбирается таким образом, чтобы при номинальной нагрузке не было опрокидывания поля под одним из краев полюсного наконечника ( < ).

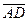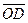При отсутствии дополнительных полюсов, когда для улучшения коммутации (§ 5-7,д) приходится щетки смешать с геометрической нейтрали, необходимо учесть размагничивающую продольную н.с. якоря F_d, которая равна (на один полюс)

F_d = cA, (5-24)

где с (см) — сдвиг щеток относительно геометрической нейтрали (рис 5-25,а). Для малых машин (< 0,5 кВт) можно принять:

c » 0,4 (t-b_d).

Таким образом, размагничивающая реакция якоря (на пару полюсов)

F_р.я. = 2 (F_qd + F_d) (5-25)

и н.с. обмотки возбуждения при нагрузке

F_в = F_E + F_р.я. (5-26)

где F_E — н.с , соответствующая э.д.с. Е_а при нагрузке (определяется по характеристике холостого хода)

5-7. Коммутация

А) Общие сведения.

Под коммутацией в собственном смысле этого слова понимают переключение секции из одной ветви обмотки якоря в другую и происходящее при этом изменение тока в ней с одного направления на другое. Процессы, возникающие при этом в секции и под щеткой, называются коммутационными процессами. Их исследование представляет собой важную задачу, так как от ее правильного решения в большой степени зависит надежность работы коллекторной машины.

Под коммутацией в широком смысле слова понимаются все явления и процессы, возникающие под щеткой при работе машины. Говорят, что у машины хорошая коммутация, если нет искрения под щетками, и плохая коммутация, если под щетками возникает искрение.

Искрение щеток вызывается различными причинами. Оно может быть обусловлено механическими неисправностями: "эллиптичностью" коллектора, плохой стяжкой его пластин, шероховатостью его поверхности, выступанием в отдельных местах слюды над коллекторными пластинами, дрожанием щеткодержателей, щеточных болтов, траверсы и пр.

При указанных неисправностях в отдельные моменты времени будет нарушаться контакт щетки с коллектором и происходить разрыв цепи с током, что и приводит к искрению.

Неправильно подобранные щетки, чрезмерное или слишком слабое нажатие щеток на коллектор, неправильная их расстановка по коллектору также могут послужить причинами искрения под щетками.

Современные способы изготовления коллектора и всей щеточной аппаратуры позволяют получить эти части машины вполне надежными и удовлетворительно работающими в отношении коммутации.

Коммутационные процессы отличаются большой сложностью, так как они протекают под влиянием многочисленных факторов. Их теоретическое исследование встречает большие затруднения и возможно только при ряде допущений. Поэтому здесь важное значение имеют правильно и тщательно поставленные эксперименты.

Много дали для понимания коммутационных процессов теоретические и особенно экспериментальные работы академика К. И. Шенфера, проф. В. Т. Касьянова и других советских ученых.

Затруднения обычно возникают при решении вопросов, связанных с коммутацией в быстроходных мощных машинах [если произведение мощности на скорость вращения близко к предельным значениям: Р·n»(2,5÷3,5)·10⁶ кВт·об/мин]. Однако в настоящее время выводы теории и главным образом большой опыт, накопленный отечественными заводами, позволяют и для таких машин эти вопросы разрешать вполне удовлетворительно.

Рассмотрим вначале изменение тока в секции обмотки якоря при его вращении. Оно представлено кривой на рис. 5-27. Когда секция находится в одной параллельной ветви, то за время прохождения ею полюсного деления ток в ней сохраняет свое значение

.

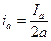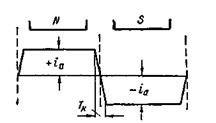
Рис. 5-27. Изменение тока в секции за время прохождения ею двух полюсных делений.

При переходе секции в другую параллельную ветвь ток в ней быстро изменяется с одного направления на другое за время Т_к замыкания ее щеткой и далее имеет то же значение i_a, пока секция не будет снова замкнута теткой. Время Т_к называется периодом коммутации. Обычно оно составляет тысячные доли секунды. Вид кривой изменения тока в секции (рис. 5-27) объясняется тем, что ток в ней, пока она не замкнута щеткой, создается постоянной э.д.с. Е_а всей параллельной ветви, а не э.д.с. одной секции.

Обратимся к рис. 5-28, где изображена секция простой петлевой обмотки, замкнутая щеткой. Будем пренебрегать толщиной изоляционной прослойки между коллекторными пластинами и примем, что ширина щетки равна ширине коллекторной пластины.

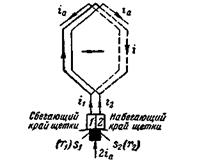
Рис. 5 28. Коммутируемая секция.

Секция, замкнутая щеткой, называется коммутируемой секцией.

В момент, когда набегающий край щетки получит соприкосновение с пластиной 2, имеем начало коммутации. Примем, что конец коммутации получается в момент, когда пластина 1 отойдет от щетки.

Будем пренебрегать сопротивлениями самой секции и соединительных проводников между секцией и коллекторными пластинами. Они незначительны по сравнению с сопротивлениями переходного контакта между щеткой и коллекторными пластинами. Обозначив сопротивления переходных контактов сбегающего и набегающего краев щетки через r₁ и r₂, составим уравнение напряжений для указанного на рис. 5-28 контура:

i₁r₁ – i₂r₂ = Se; (5-27)

здесь Se — сумма э.д.с., наведенных в коммутируемой секции. В эту сумму входят э.д.с. самоиндукции и взаимной индукции (рис. 5-29) и э.д.с. внешнего поля, имеющего место в коммутационной зоне, причем под последней понимается та часть поверхности якоря, где лежат стороны коммутируемых секций.

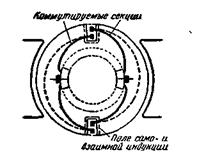
Рис. 5-29. Коммутируемые секции.

Подставив в (5-27) равенства (рис. 5-28)

i₁ = i_a + i; (5-28)

i₂ = i_a - i, (5-29)

получим:

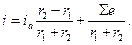(5-30)

Примем, что r₁ и r₂ не зависят от плотности тока и что они обратно пропорциональны площадям соприкосновения соответственно сбегающего края щетки S₁, и набегающего края щетки S₂:

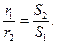(5-31)

Площадь S₂ пропорциональна времени t, протекшему от начала коммутации, а площадь S₁ — времени Т_к - t, оставшемуся до конца коммутации. Поэтому можем написать:

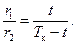(5-32)

В действительности r₁ и r₂ зависят от плотности тока, так как ток проходит не только через точки непосредственного соприкосновения щетки с коллекторными пластинами, но и через тонкие воздушные прослойки между ними, в которые к тому же попадает увлажненный воздух. Следовательно, мы здесь имеем также ионные процессы, в том числе и электролитические, которые не могут быть точна рассчитаны. Кроме того, надо отметить нестабильность контакта щетки с коллекторными пластинами, в особенности ее сбегающего края, что приводит к изменению периода коммутации, отличающегося в действительности от его расчетного значения Т_к. Принятое нами допущение позволяет все же проследить приближенно процессы с их качественной стороны и получить некоторые исходные данные для расчета дополнительных полюсов, которые могут быть уточнены опытной проверкой.