Волновая функция и ее статистический смысл
Экспериментальное подтверждение гипотезы де Бройля о корпус-кулярно-волновом дуализме, ограниченность применения законов классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также невозможность в рамках классической электродинамики объяснить ряд экспериментальных фактов (фотоэффект, эффект Комптона и др.) привело к созданию квантовой механики, описывающей законы движения микрочастиц с учетом их волновых свойств.
Поведение фотона (электромагнитной волны) описывается уравнением:
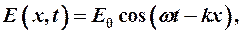
так как
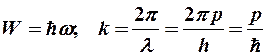 ,
,
тогда
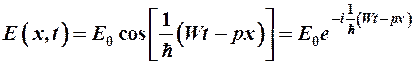 (6-4)
(6-4)
где 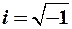 - мнимая единица.
- мнимая единица.
Поведение микрочастицы можно описать аналогично:
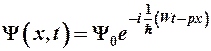 (6-5)
(6-5)
где 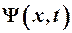 - Пси-функция (или волновая функция) – математическое выражение, описывающее поведение микрочастицы;
- Пси-функция (или волновая функция) – математическое выражение, описывающее поведение микрочастицы;
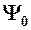 - амплитуда волновой функции;
- амплитуда волновой функции;
W и p – энергия и импульс микрочастицы.
Установим физический смысл волновой функции.
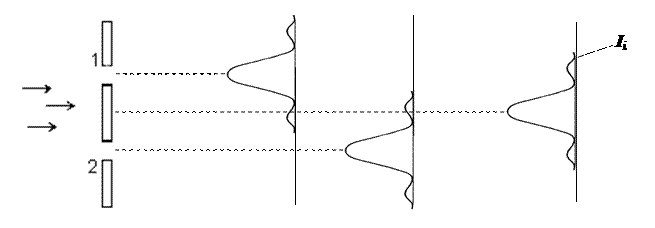 Рассмотрим аналогию между дифракцией света и дифракцией электронов на двух щелях.
Рассмотрим аналогию между дифракцией света и дифракцией электронов на двух щелях.
Для фотонов (электромагнитной волны):
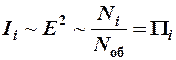 ®
® 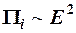
Для электронов:
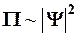 ,
,
так как Y может быть комплексной, а вероятность P всегда действи-тельная величина.
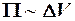 , DV – объем области на экране, куда попадают частицы.
, DV – объем области на экране, куда попадают частицы.
Тогда 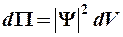
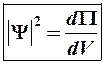 (6-6)
(6-6)
Квадрат модуля волновой функции определяется плотностью вероятности пребывания микрочастицы в элементе объема dV, то есть в объеме с координатами x + dx, y + dy, z + dz.
Таким образом, физическим смыслом обладает не сама волновая функция, а квадрат ее модуля.
И так как 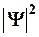 носит вероятностный характер, то волновую функцию
носит вероятностный характер, то волновую функцию 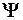 иногда называют амплитудой вероятности.
иногда называют амплитудой вероятности.
(Так как теория вероятностей используется в статистической физике, то формула (6-6) определяет физический или статистический смысл 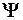 -функции).
-функции).

Из этого определения волновой функции следуют ее свойства:
1) однозначность (вероятность имеет одно значение);
2) конечность (вероятность – конечная величина £ 100%);
3) непрерывность (вероятность не должна иметь точек разрыва);
4) условие нормировки 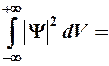 1. ®
1. ® 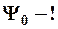
Дата добавления: 2016-01-18; просмотров: 1443;
