Корпускулярно-волновой дуализм вещества
В 1924 г. французский физик-теоретик Луи де Бройль выдвинул гипотезу:
всякая движущаяся частица подобно фотону обладает волновыми свойствами (сама является волной).
Значит, для нее можно вычислить длину волны по аналогии с формулой (5-2) для импульса фотона:
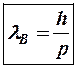, (6-1)
где р – импульс частицы.
В нерелятивистском случае
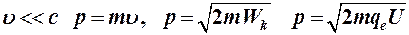
Для больших скоростей
u d с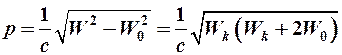 
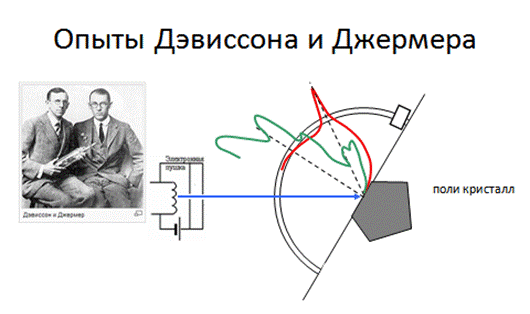
Только спустя 3 года гипотеза де Бройля была экспериментально подтверждена
1927 г. - Джермер и Девиссон
- Томсон и Тартаковский
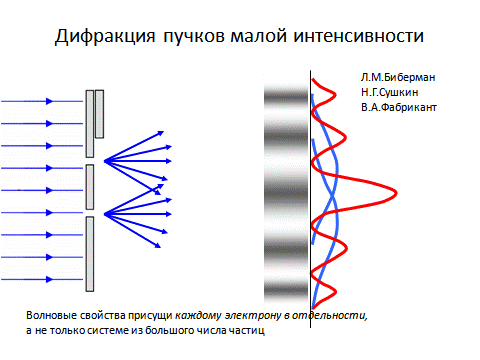
1949 г. - Биберман, Сушкин, Фабрикант
Таким образом, корпускулярно-волновой дуализм вещества предполагает, что у любого объекта есть потенциальная возможность проявить себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом.
Так, например, для частицы массой 1 г, движущейся со скоростью 1 м/с lВ= 6,63×10-31 м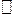 
доступной наблюдению области (таких структур просто не существует).
А вот, например, для электрона (m ~ 10-30 кг), движущегося в атоме со скоростью u ~ 106 м/с получаем l ~ 10-10 м, что соответствует как раз размеру атома, где и «живет» электрон.
Поэтому для того, чтобы определить существенны ли волновые свойства у частицы или нет, нужно вычислить дебройлевскую длину волны этой частицы и сравнить ее с каким-либо характерным размером в задаче L. Если lВ << L,то такая частица практически не проявляет свои волновые свойства и для описания ее поведения можно использовать законы классической или релятивистской механики. А вот если lВ ~ L, тогда для описания поведения такой частицы требуются уже другие законы (законы квантовой (волновой) механики).
Итак, для описания микрочастиц используются то корпускулярные, то волновые представления. Поэтому приписывать частицам все свойства волн или все свойства частиц нельзя. Необходимы ограничения в применении к микрочастицам законов классической механики.
Классическая механика считает, что если частица движется по определенной траектории, то в любой момент времени ее координаты и импульс достаточно точно известны:
.
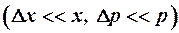Для микрочастиц, из-за наличия у них волновых свойств, неправомерно говорить о точных значениях координаты и импульса (так, понятие «длина волны в данной точке» лишено физического смысла, а так как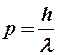 
, то и импульс частицы точно не определен).
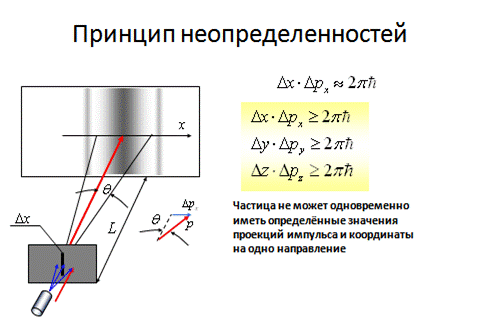
Немецкий физик Гейзенберг в 1927 году сформулировал принцип (соотношение) неопределенностей:
микрочастица не может одновременно иметь и точную координату и точное значение импульса, при этом неопределенности (погрешности) этих величин должны удовлетворять условию:
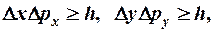DzDpz 
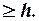(6-2)
то есть произведение неопределенностей координаты на соответствующую ей проекцию неопределенности импульса не может быть меньше величины порядка h.
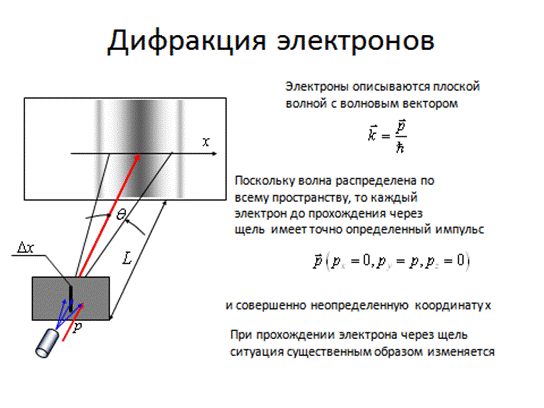
Так как погрешности измерения скорости любой частицы Du << u (предельная Du << c = 3×108 м/с),тогда, например, для электрона(m ~10-30 кг) имеем:
м.
Т. е., например, в ядре атома, размер которого ~ 10-15 м, электрон не может находиться, а вот внутри атома, размер которого ~ 10-10 м, такое возможно (электрон, как раз, и «живет» в атоме!)
В квантовой физике рассматривается также соотношение неопре-деленностей для энергии W и времени t, то есть неопределенности этих величин определяются условием:
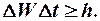(6-3)
где DW - неопределенность энергии некоторого состояния системы;
Dt - промежуток времени, в течение которого это состояние существует.
Дата добавления: 2016-01-18; просмотров: 1705;