Волновая поверхность
Волновое уравнение
Пусть в некоторой области пространства нет частиц, способных переносить заряды (r=0 и 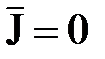 ) и поляризоваться (
) и поляризоваться ( 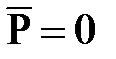 и
и 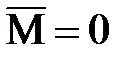 ). Назовем такую среду пустым пространством или вакуумом.
). Назовем такую среду пустым пространством или вакуумом.
Систему уравнений Максвелла для пустого пространства можно записать в очень стройной симметричной форме:
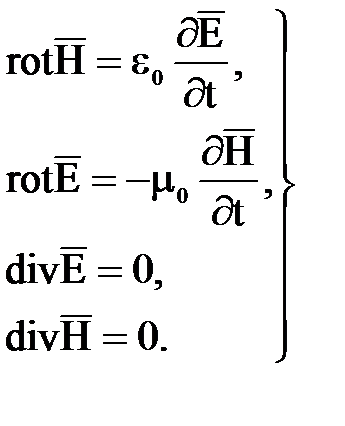 (7.1)
(7.1)
Известно, что основные уравнения поля можно записать через электродинамические потенциалы 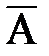 и j. Для области пространства, где нет свободных зарядов (r=0), можно принять j=0. Можно показать, что такой выбор скалярного потенциала не противоречит системе (7.1), но накладывает дополнительное условие на дивергенцию векторного потенциала
и j. Для области пространства, где нет свободных зарядов (r=0), можно принять j=0. Можно показать, что такой выбор скалярного потенциала не противоречит системе (7.1), но накладывает дополнительное условие на дивергенцию векторного потенциала
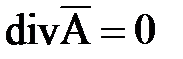 , (7.2)
, (7.2)
вытекающее из уравнения «калибровки» 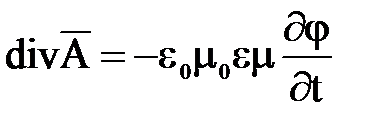 .
.
Выбор j=0 удобен тем, что при этом уравнение для скалярного потенциала 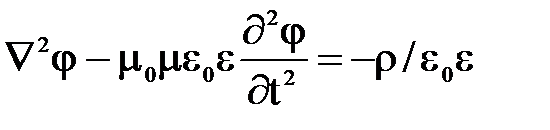 обращается в тождество, а уравнение для векторного потенциала можно записать в такой форме:
обращается в тождество, а уравнение для векторного потенциала можно записать в такой форме:
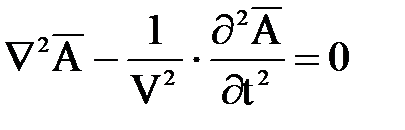 , (7.3)
, (7.3)
где 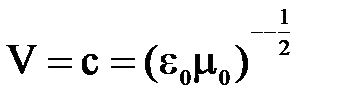 - скорость света.
- скорость света.
Уравнения такой структуры называются волновыми, а их решения волнами.
Если найдено решение для вектора 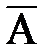 , то нетрудно найти напряженность электрического и магнитного поля.
, то нетрудно найти напряженность электрического и магнитного поля.
Из выражений 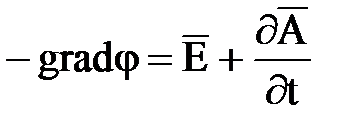 и
и 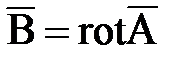 , учитывая, что j=0 и m=1, получим
, учитывая, что j=0 и m=1, получим
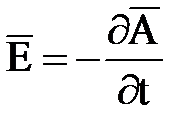 и
и 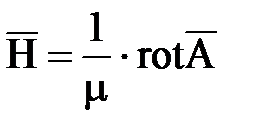 . (7.4)
. (7.4)
В некоторых случаях удобнее искать решения уравнений, непосредственно записанных для векторов 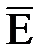 и
и 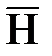 . Такие уравнения можно получить из (7.1), исключив один из неизвестных векторов. Например, если вычислить ротор левой и правой части второго уравнения, получим
. Такие уравнения можно получить из (7.1), исключив один из неизвестных векторов. Например, если вычислить ротор левой и правой части второго уравнения, получим
rot 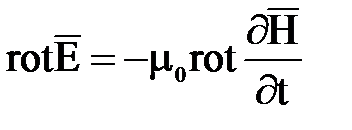 или grad
или grad 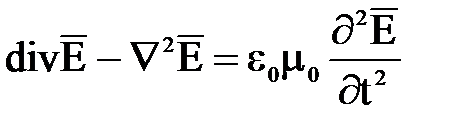 .
.
К левой части применено известное правило векторного анализа (rot 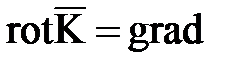
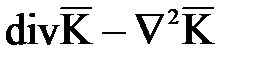 ), a в правой - сделана подстановка значения
), a в правой - сделана подстановка значения  из второго уравнения системы (7.1). Учитывая, что
из второго уравнения системы (7.1). Учитывая, что 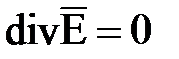 , после элементарных преобразований получим
, после элементарных преобразований получим
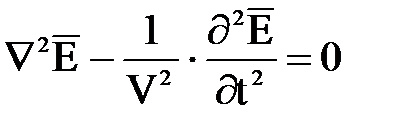 . (7.5)
. (7.5)
Совершенно аналогично можно получить
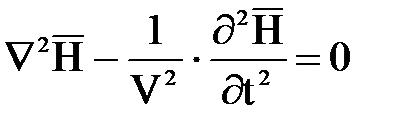 . (7.6)
. (7.6)
В заключение отметим, что электромагнитные волны не могут существовать, если векторы поля не изменяются во времени. Это следует из системы (7.1). Если производные по времени равны нулю, то поле не будет иметь ни вихрей, ни истоков, т. е. тождественно будет равно нулю.
Волновая поверхность
Волновые гармонические процессы характеризуется амплитудой, частотой и фазой. В случае волновых процессов фаза колебания в рассматриваемой точке наблюдения определяется не только временем t , но и удалением этой точки от источника волн или начала отсчета расстояния Z, а также скоростью распространения электромагнитных колебаний.
E=Emcos(wt-w 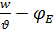 )
)
ϑ- скорость распространения колебания.
Кроме фазы и скорости распространения электромагнитные волны характеризуются длиной, формой волновой поверхности и поляризацией.
Волновой (фазовой) поверхностью называется поверхность во всех точках которой основные векторы поля 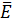 и
и 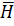 имеют одну и ту же фазу. В которой фиксированной точке пространства E и H применяются во времени, а следовательно волновая поверхность перемещается с некоторой скоростью. Скорость перемещения волновой поверхности называется фазовой скоростью ϑ В зависимости от формы волновой поверхности волны могут быть плоскими, сферическими и цилиндрическими.
имеют одну и ту же фазу. В которой фиксированной точке пространства E и H применяются во времени, а следовательно волновая поверхность перемещается с некоторой скоростью. Скорость перемещения волновой поверхности называется фазовой скоростью ϑ В зависимости от формы волновой поверхности волны могут быть плоскими, сферическими и цилиндрическими.
1. Плоская волна.
C=Cmcos(wt-w 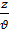 )
)
C=Cmcos*w(t-w 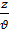 )
)
где C=Cm(z) - амплитуды векторов 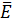 и
и 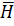 в общем случае, зависящие от Z
в общем случае, зависящие от Z
При заданной частоте и фиксированном моменте времени t=t0 фаза
Φ=w(t0- 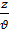 ) если Z=const .
) если Z=const .
Таким образом, волновыми поверхностями волны, определяемой выражением (3) является плоскости Z=const, параллельные координатной плоскости XOY
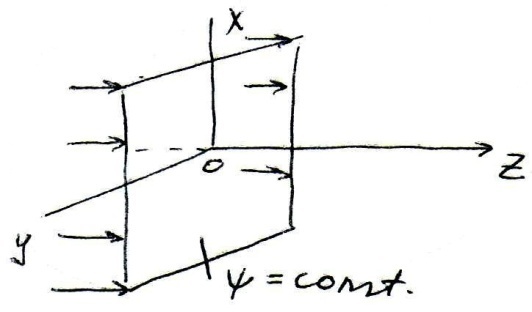
Плоской волне соответствует следующие комплексные выражения:
c(t)=cm 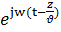 =cm(z)
=cm(z) 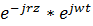
r – волновое число.
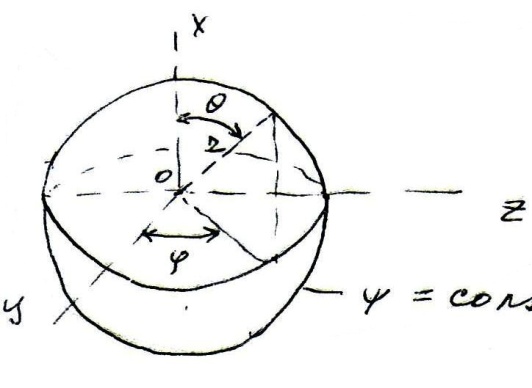
Сферическая волна.
c= 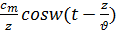
где cm= cm(z,Q,φ)- модуль вектора поля, в общем случае зависящий от сферических координат точки наблюдения.
Поверхностями равных фаз в этом случае являются сферы, так как φ=w(t0- 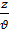 )=const при z=const .
)=const при z=const .
Следовательно сферической электромагнитной волной называется такая волна, поверхностью равной фазы которой является сфера. Сферической волне соответствуют следующие комплексные выражения.
 (t)=
(t)= 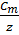
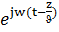 =
= 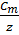
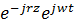
 m=
m= 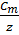
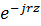
| <== предыдущая лекция | | | следующая лекция ==> |
| Фотохимические реакции. Основные законы фотохимии | | | Общая характеристика и классификация каталитических реакций |
Дата добавления: 2015-12-16; просмотров: 1476;
