Б) Уравнения напряжений.
Будем вначале считать, что потокосцепления обмоток трансформатора пропорциональны их токам и что магнитные потери в сердечнике отсутствуют (такие условия получаются в воздушном трансформаторе). При этом, так же как для двух магнитно связанных контуров, можем написать следующие уравнения напряжений первичной и вторичной обмоток трансформатора:
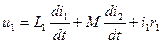 ; (2-20)
; (2-20)
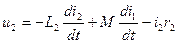 , (2-21)
, (2-21)
где u1 и u2 — мгновенные значения первичного и вторичного напряжений;
L1, L2 и М — полные индуктивности и взаимная индуктивность обмоток;
r1 и r2 — их активные сопротивления.
Первичное напряжение u1 имеет составляющие, уравновешивающие э.д.с. cамоиндукции 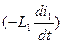 и взаимоиндукции
и взаимоиндукции 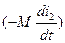 , и составляющую, равную активному падению напряжения i1r1. Вторичное напряжение u2 получается после вычитания из результирующей э.д.с. самоиндукции и взаимоиндукции
, и составляющую, равную активному падению напряжения i1r1. Вторичное напряжение u2 получается после вычитания из результирующей э.д.с. самоиндукции и взаимоиндукции 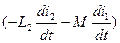 активного падения напряжения i2r2.
активного падения напряжения i2r2.
Полагая, так же как и в предыдущем, что в сердечнике трансформатора имеет место главный поток Ф, который создается результирующей н.с. i0w1 мы можем для токов i1, и i2 согласно (2-14) написать следующие равенства:
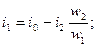 (2-22)
(2-22)
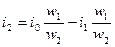 (2-23)
(2-23)
Подставив (2-23) в (2-20) и (2-22) в (2-21), получим:
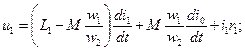 (2-24)
(2-24)
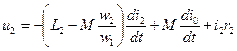 (2-25)
(2-25)
или
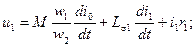 (2-24a)
(2-24a)
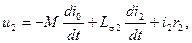 (2-25a)
(2-25a)
где 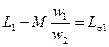 и
и 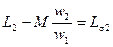 — индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э.д.с. рассеяния:
— индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э.д.с. рассеяния:
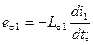 ; (2-26)
; (2-26)
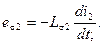 (2-27)
(2-27)
Электродвижущие силы
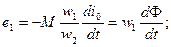 (2-28)
(2-28)
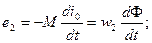 (2-29)
(2-29)
рассматриваются как э.д.с., наведенные главным потоком Ф.
Приведем здесь уравнения, относящиеся к общей теории двух магнитно связанных обмоток. Для потокосцеплении этих обмоток можем написать:
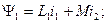 (2-30)
(2-30)
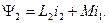 (2-31)
(2-31)
Вычтем и прибавим с правой стороны написанных равенств одни и те же величины:
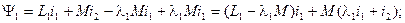
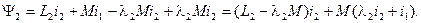
Здесь коэффициенты 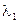 и
и 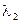 имеют произвольные значения.
имеют произвольные значения.
Будем называть величины
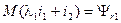 и
и 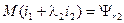
главными потокосцеплениями обмоток, а величины
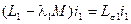 и
и 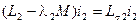
их потокосцеплениями рассеяния.
Главными индуктивностями обмоток назовем величины
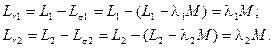
Общий коэффициент рассеяния равен:
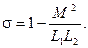 (2-32)
(2-32)
Коэффициенты рассеяния обмоток равны отношениям индуктивностей рассеяния к главным индуктивностям:
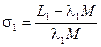 и
и 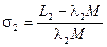 . (2-33)
. (2-33)
Между произвольными значениями коэффициентов λ1 и λ2 можно установить простое соотношение. Для этого примем (с физической стороны это легко себе представить), что общий коэффициент рассеяния стремится к нулю (σ → 0), если при этом индуктивности рассеяния стремятся к нулю. Вводя 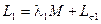 и
и 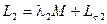 в (2-32) и принимая
в (2-32) и принимая 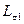 и
и 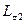 равными нулю, получим для σ → 0:
равными нулю, получим для σ → 0:
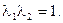 (2-34)
(2-34)
Отсюда имеем: 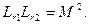
Мы видим, следовательно, что, хотя общий коэффициент рассеяния σ определяется однозначно, отдельные коэффициенты рассеяния σ1 и σ2 являются произвольными, так же как λ1 и λ2.
Подразделяя произведение λ1λ2 любым образом на λ1 и λ2 можно потокосцепления рассеяния приписать одной или другой обмотке или обеим обмоткам. Мы не имеем также достаточно данных, чтобы однозначно определить главный поток, о котором говорилось ранее. Однако внести определенность в понятия индуктивностей рассеяния мы можем только в том случае, если допустим, что в трансформаторе существует главный поток Ф, созданный н.с. обеих обмоток и сцепляющийся со всеми их витками. Такое допущение, очевидно, в большой степени оправдывается в применении к нормальным трансформаторам со стальным сердечником.
Мы можем теперь написать:
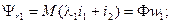
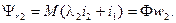
Отсюда получаем:
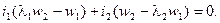
Так как полученное равенство должно быть справедливо при любых значениях 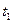 и
и 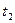 , то выражения в скобках по отдельности должны быть равны нулю; следовательно,
, то выражения в скобках по отдельности должны быть равны нулю; следовательно, 
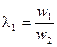 и
и 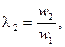 что мы и получили ранее в дифференциальных уравнениях, допустив, что в трансформаторе существует главный поток Ф, созданный результирующей н.с.
что мы и получили ранее в дифференциальных уравнениях, допустив, что в трансформаторе существует главный поток Ф, созданный результирующей н.с. 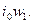
Теория электрических машин также основана, как мы покажем в дальнейшем, на допущении существования главного потока, не зависящего от полей рассеяния.
Считая, что токи и э.д.с. уравнений (2-26)—(2-29) изменяются во времени по закону синуса, мы можем эти уравнения переписать в комплексной форме:
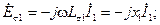
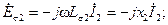
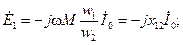 (2-35)
(2-35)
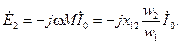
В равенствах (2-35) 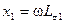 и
и 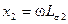 — индуктивные сопротивления рассеяния обмоток, а
— индуктивные сопротивления рассеяния обмоток, а 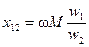 — индуктивное сопротивление взаимоиндукции обмоток.
— индуктивное сопротивление взаимоиндукции обмоток.
Ранее при рассмотрении режима холостого хода мы пренебрегали полем вне сердечника трансформатора. В действительности это поле согласно закону полного тока должно существовать. Оно называется полем рассеяния. Созданные им потокосцепления обмоток малы по сравнению с потокосцеплениями обмоток, созданными главным потоком. С большим приближением к действительным условиям можно считать, что поле рассеяния и поле в сердечнике, соответствующее главному потоку, существуют независимо одно от другого.
На рис. 2-13 представлена приближенная картина поля рассеяния, которую кладут в основу расчета потокосцеплений рассеяния. Здесь пунктирной линией показан путь главного потока Ф, сплошными линиями показаны индукционные линии поля рассеяния. Они могут быть условно разделены на две группы: сцепляющиеся с первичной обмоткой и сцепляющиеся со вторичной обмоткой. Магнитные сопротивления для потоков соответствующих индукционных трубок рассеяния определяются в основном сопротивлениями тех их частей, которые проходят вдоль обмоток и в промежутке между ними Их можно принять постоянными, поскольку потоки трубок проходят по материалам (медь, изоляция, воздух или масло), для которых μ = const. Магнитными сопротивлениями потоков трубок вне обмоток и промежутка между ними можно пренебречь, так как здесь они проходят в основном по стали сердечника.
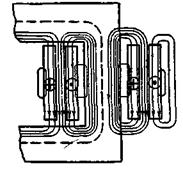
Рис. 2-13. Приближенная картина поля рассеяния трансформатора с концентрическими обмотками, где крестиками и точками условно показаны направления токов в обмотках для рассматриваемого момента времени.
Таким образом, потокосцепления рассеяния и созданные ими э.д.с. рассеяния можно принять пропорциональными н.с. или токам соответствующих обмоток и считать индуктивности Lσ1 и Lσ2, а следовательно 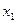 и
и 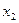 , постоянными величинами. Индуктивное сопротивление взаимоиндукции
, постоянными величинами. Индуктивное сопротивление взаимоиндукции 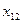 зависит от Ф, однако в пределах небольшого изменения Фм и, следовательно, Е1 можно принять
зависит от Ф, однако в пределах небольшого изменения Фм и, следовательно, Е1 можно принять 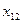 также постоянным.
также постоянным.
С учетом приведенных равенств (2-35) уравнения напряжений (2-24а) и (2-25а) для установившегося режима могут быть написаны в комплексной форме:
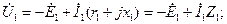 (2-36)
(2-36)
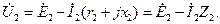 (2-37)
(2-37)
Уравнения (2-36) и (2-37) называются векторными уравнениями напряжений трансформатора (здесь имеются в виду временные векторы напряжений, э.д.с. и токов).
В реальном трансформаторе со стальным сердечником при его работе возникают магнитные потери. Для их учета мы должны считать, так же как при холостом ходе, что ток 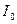 имеет наряду с реактивной составляющей
имеет наряду с реактивной составляющей 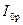 активную составляющую
активную составляющую 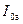 [см. уравнения (2-9) — (2-13)]; однако обе эти составляющие мы должны отнести не к
[см. уравнения (2-9) — (2-13)]; однако обе эти составляющие мы должны отнести не к 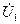 а к
а к 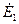 , так как они зависят от Фм.
, так как они зависят от Фм.
Вследствие нелинейной связи между потоком Ф и результирующим током 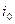 кривая последнего при синусоидальном потоке Ф будет несинусоидальной (§ 2-13). Для облегчения анализа зависимостей, характеризующих работу трансформатора, ток
кривая последнего при синусоидальном потоке Ф будет несинусоидальной (§ 2-13). Для облегчения анализа зависимостей, характеризующих работу трансформатора, ток 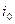 принимается синусоидальным с действующим значением, равным тому же значению действительного тока. Такое допущение не может привести к заметной ошибке из-за относительной малости тока
принимается синусоидальным с действующим значением, равным тому же значению действительного тока. Такое допущение не может привести к заметной ошибке из-за относительной малости тока 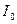 .
.
Дата добавления: 2016-01-29; просмотров: 2342;
