Г) Векторные диаграммы.

Векторные диаграммы наглядно показывают соотношения между токами, э.д.с. и напряжениями обмоток. Они строятся в соответствии с уравнениями (2-19), (2-36) и (2-38).

На рис. 2-14 — 2-16 представлены диаграммы трансформатора, работающего с различными нагрузками.

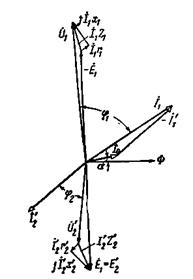
Рис. 2-14. Векторная диаграмма трансформатора работающего с отстающим током.

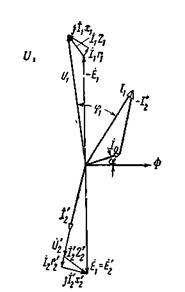
Рис. 2-15. Векторная диаграмма трансформатора, работающего с 1.

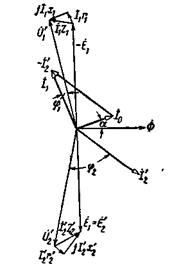
Рис. 2-16. Векторная диаграмма трансформатора, работающего с опережающим током.

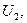
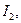
Векторная диаграмма трансформатора, работающего, например, с отстающим током (рис. 2-14), при заданных 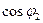может быть построена следующим образом.

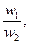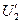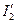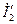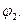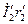Зная найдем и . Построим в выбранном масштабе для токов и напряжений векторы и так, чтобы они были сдвинуты на угол Прибавляя к векторы падений напряжения и 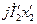найдем э.д.с. 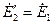(мы предполагаем, что сопротивления 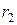и 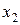, а также 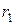и и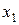звестны). Вектор потока 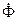опережает э.д.с. 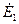на 90°. Ток 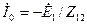опережает поток на угол 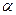. Вторая составляющая 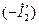первичного тока 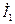равна и противоположна по фазе вторичному току 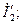следовательно, вектор первичного тока определяется геометрическим сложением: 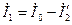. Первичное напряжение 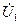, имеет составляющую 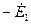, уравновешивающую э.д.с. 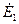, и составляющие 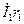и 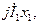равные соответственно активному и индуктивному падениям напряжения в первичной обмотке ( 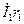совпадает по фазе с током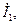 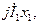опережает ток 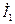на 90°).

Обратная задача, с которой обычно приходится иметь дело на практике, когда заданы 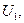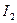и cos φ₂ и требуется найти 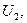решается в большинстве случаев аналитически, как показано в § 2-8.

Диаграммы на рис. 2-14 и 2-15 показывают, что напряжение 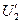при нагрузке меньше, чем напряжение 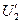при холостом ходе, и тем меньше, чем больше сопротивления обмоток r₁, x₁, r₂, и угол φ₂.

Значение тока 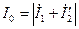зависит от значения э.д.с. 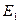; следовательно, оно изменяется с изменением тока нагрузки, если 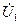= const. Однако это изменение невелико, и при практических расчетах можно принять Ф_м=const и 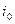=const.

Диаграмма на рис. 2-16 показывает, что при работе трансформатора с опережающим током напряжение 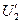на его зажимах может быть выше, чем при холостом ходе, так как в этом случае э.д.с. 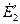возрастает и, кроме того, результирующая э.д.с. 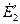+ 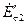больше, чем 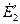( 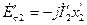― э.д.с. рассеяния вторичной обмотки, приведенная к числу витков первичной обмотки).

Приведенные ранее уравнения напряжений и токов, а также векторные диаграммы относятся к однофазному трансформатору или к одной фазе трехфазного трансформатора. Различие токов холостого хода отдельных фаз трехфазного трансформатора вследствие несимметрии их магнитных цепей не имеет практического значения, так как токи холостого хода составляют обычно небольшую долю номинального тока; параметры же отдельных фаз r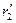₁, , x₁, 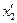можно считать одинаковыми.

2-5. Схема замещения

Расчеты, связанные с исследованием работы трансформатора, можно свести к расчетам простых цепей переменного тока. Для этого заменим трансформатор некоторой схемой, сопротивление которой Z_экв определим; из уравнений напряжений (2-36) и (2-38) и уравнения токов (2-17). Перепишем эти уравнения в следующем виде:

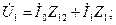(2-40)

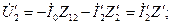(2-41)

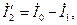(2-42)

где 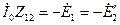[см. уравнение (2-12)];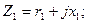

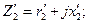
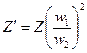― приведенное к числу витков первичной обмотки сопротивление внешней вторичной цепи, падение напряжения 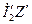в котором, очевидно, и есть .

Подставив в (2-41) значение тока 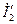из (2-42), найдем:

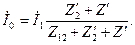
Подставив в (2-40) найденное значение 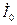, получим:

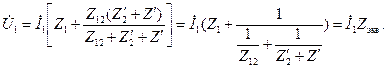(2-43)

Сопротивлению Z_экв соответствует схема, представленная на рис. 2-17. Она называется схемой замещения трансформатора. Здесь ветвь с сопротивлением 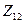может быть названа ветвью намагничивания. Очевидно, что уравнения напряжений и токов, составленные согласно законам Кирхгофа для этой схемы, будут такими же, как и уравнения (2-40) — (2-42).

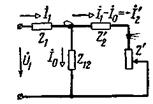
Рис. 2-17. Схема замещения трансформатора.

В схеме замещения переменным параметром является сопротивление 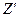; остальные ее параметры можно считать постоянными. Они могут быть определены путем расчета, а также опытным путем. В последнем случае обращаются к данным опытов холостого хода и короткого замыкания.

2-6. Опыт холостого хода

По данным опыта холостого хода определяются коэффициент трансформации 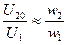, магнитные потери Р_с и параметры ветви намагничивания 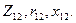Магнитные потери Р_с, как указывалось, могут быть приняты равными мощности Р₀, потребляемой трансформатором при холостом ходе.

При опыте холостого хода собирается схема по рис. 2-18 для однофазного трансформатора или по рис. 2-19 для трехфазного трансформатора. При номинальном напряжении 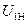(линейном в случае трехфазного трансформатора) измеряют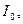 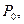и 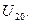Опыт холостого хода должен производиться при синусоидальном напряжении. Если напряжение заметно отличается от синусоидального, то в данные измерений необходимо внести некоторые поправки (согласно ГОСТ). При исследовании малых трансформаторов следует учитывать потери в приборах, так как они могут быть соизмеримы с потерями холостого хода.

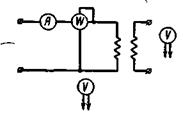
Рис. 2-18 Схема при опыте холостого хода для однофазного трансформатора.

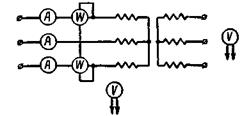
Рис. 2-19. Схема при опыте холостого хода для трехфазного трансформатора.

Измерения U₁ и U₂₀ производятся при помощи вольтметров или при высоком напряжении, при помощи вольтметров и измерительных трансформаторов напряжения. По данным измерений находят коэффициент трансформации: U₂₀/U₁ 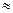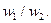По амперметру и ваттметру находят ток 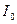и мощность P₀ в случае однофазного трансформатора. В случае трехфазного трансформатора необходимо измерить токи во всех трех фазах, так как вследствие несимметрии магнитных цепей отдельных фаз токи в них будут различны. За ток холостого хода здесь принимается среднее арифметическое токов отдельных фаз, т. е.

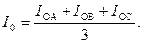(2-44)

Мощности отдельных фаз также различны; поэтому мощность, потребляемую трехфазным трансформатором при холостом ходе, следует измерять двумя ваттметрами по схеме рис. 2-19.

Для нормальных силовых трансформаторов ток холостого хода составляет (0,10—0,04) I_Н при номинальных мощностях от 5 до нескольких тысяч киловольт-Ампер.

Холостому ходу будет соответствовать схема замещения рис. 2-17 при 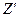=∞. Следовательно, по данным опыта холостого хода получаем:

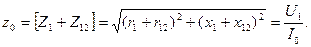
Так как для нормальных трансформаторов r₁₂ больше r₁ и x₁₂ больше х₁ в сотни раз, то можно принять:

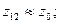
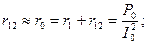
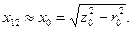
2-7. Опыт короткого замыкания

По данным опыта короткого замыкания определяются потери короткого замыкания Р_к, которые могут быть приняты равными электрическим потерям в обмотках, и параметры трансформатора, к которым приходится обращаться при решении многих практических задач.

Под коротким замыканием трансформатора здесь понимается такой режим его работы, при котором вторичная обмотка замкнута накоротко, а к первичной обмотке подведено напряжение. Этому режиму работы соответствует схема замещения (рис. 2-17) при 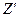=0.

Так как сопротивления z₁ и 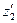в сотни раз меньше сопротивления z₁₂, то при коротком замыкании трансформатора можно пренебречь током в этом сопротивлении, т. е. принять 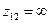. В этом случае получаем схему замещения, представленную на рис. 2-20.

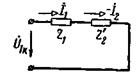
Рис. 2-20. Схема замещения короткозамкнутого трансформатора.

Векторная диаграмма короткозамкнутого трансформатора приведена на рис. 2-21.

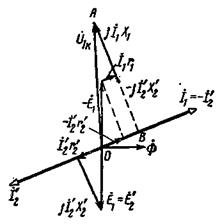
Рис. 2-21. Векторная диаграмма короткозамкнутого трансформатора.

От этой диаграммы мы можем перейти к диаграмме, представленной на рис. 2-22.

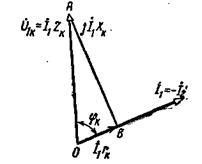
Рис. 2-22. Треугольник короткого замыкания.

Прямоугольный треугольник ОАВ называется треугольником короткого замыкания трансформатора. Один его катет 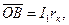другой катет 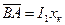и гипотенуза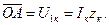

Сопротивления

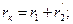
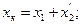
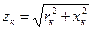
называются соответственно активным, индуктивным и полным сопротивлениями короткого замыкания трансформатора. Параметры короткого замыкания z_к, r_к и x_к определяются по данным опыта короткого замыкания. При этом опыте собирается одна из схем, приведенных на рис. 2-18 и 2-19, но вторичные зажимы замыкаются накоротко. Измеряют U_1к, I₁, P_к. Напряжение U_1к устанавливают такое, чтобы ток 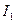был приблизительно равен номинальному току 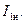Оно для нормальных трансформаторов мощностью от 20 до 10000 кВА составляет от 5 до 10% номинального напряжения 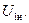В соответствии с указанными значениям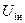и и 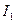подбирают при опыте короткого замыкания измерительные приборы.

Так как при этом опыте 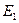а следовательно, и поток Ф (E₁ ≈ 0,5 U_1к, рис. 2-21) составляют всего несколько процентов от их значений при номинальном напряжении (а потери в стали приблизительно пропорциональны Ф²), то магнитными потерями можно пренебречь и считать, что мощность P_к, потребляемая трансформатором при коротком замыкании, идет на покрытие электрических потерь в обмотках трансформатора:

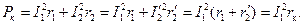(2-45)

Отсюда находим:

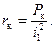(2-46)

Согласно ГОСТ активные сопротивления обмоток трансформаторов, по которым определяются электрические потери и активные падения напряжения, должны быть приведены к температуре 75° С. Это приведение делаем согласно соотношению

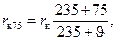(2-47)

где 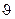— температура обмоток, °С, при опыте короткого замыкания.

Далее определяем:

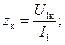
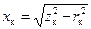
(можно принять, что 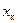от температуры не зависит) и

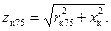
После этого определяем номинальное напряжение короткого замыкания U_к = I_1нz_к75. Оно, очевидно, равно напряжению, которое, будучи приложено к одной обмотке трансформатора при замкнутой накоротко его другой обмотке, создаст в обеих обмотках номинальные токи.

Напряжение U_к = I_1нz_к75 выражается в процентах номинального напряжения той обмотки, со стороны которой производились измерения при опыте короткого замыкания:

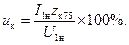(2-48)

Процентное значение номинального напряжения короткого замыкания указывается на щитке трансформатора. Оно для нормальных трансформаторов лежит в пределах 5 — 10%. Также выражаются в процентах номинального напряжения реактивная и активная составляющие напряжения короткого замыкания:

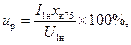(2-49)
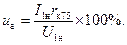(2-50)

Если числитель и знаменатель правой части равенства (2-50) умножить на I_1н и число фаз т, то получим:

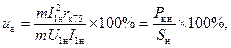(2-51)

т. е. 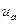в то же время дает процентное значение электрических потерь в обмотках трансформатора или потерь короткого замыкания при номинальных токах.

Значения r₁ и r₂ могут быть измерены при постоянном токе, например при помощи амперметра и вольтметра Полученные при этом сопротивления будут несколько меньше активных сопротивлений обмоток. Активные сопротивления больше сопротивлений, измеренных при постоянном токе, в 1,03 — 1,07 раза вследствие наличия вихревых токов в проводниках обмоток и в других металлических частях трансформатора, вызванных полями рассеяния.

Определить отдельно значения х₁ и x₂ довольно трудно. Практически достаточно найти только х_к.

2-8. Изменение вторичного напряжения

Вторичное напряжение 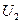при нагрузке в общем случае отличается от вторичного напряжения U₂₀ при холостом ходе. Изменение вторичного напряжения при переходе от холостого хода к нагрузке при 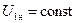принято выражать в процентах номинального напряжения.

Полученное значение

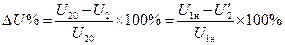(2-52)

называется процентным изменением напряжения трансформатора. Оно может быть найдено при помощи векторной диаграммы, представленной на рис. 2-23 и соответствующей схеме замещения на рис. 2-24.

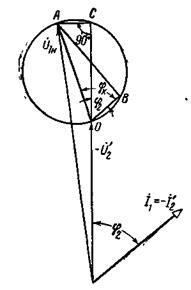
Рис. 2-23. Упрощенная векторная диаграмма трансформатора (для определения изменения напряжения).

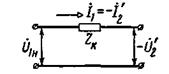
Рис. 2-24. Упрощенная схема замещения (для определения изменения напряжения).

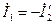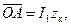
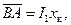
При построении диаграммы мы пренебрегли током I₀, так как он не превышает 5—10% номинального тока (при этом ). На диаграмме ∆ОАВ — треугольник короткого замыкания со сторонами 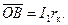Из точки А мы опустили перпендикуляр 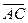на продолжение вектора .

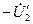Теперь можем написать:

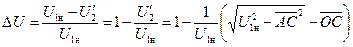(2-53)

или

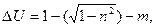(2-54)

где 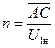и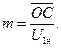

Так как n составляет в обычных случаях небольшую долю единицы, то можно воспользоваться приближенным равенством 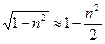. Подставляя в (2-54) приближенное значение радикала, получим: 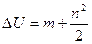или в процентах

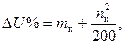(2-55)

где m_к = m·100 и n_к = n·100. Значения m_к и n_к можно найти при помощи графического построения, представленного на рис. 2-25. Здесь 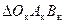— треугольник короткого замыкания, стороны которого выражены в процентах от номинального напряжения:

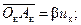
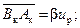
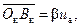(2-56)

где

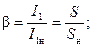(2-57)

значения u_к и u_o и u_а рассчитываются по (2-48), (2-49) и (2-50). На гипотенузе 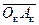как на диаметре построим окружность Проведем линию 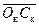под заданным углом 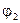к катету 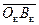до пересечения с этой окружностью. Отсюда найдем искомые значения m_к и n_к:

; .

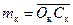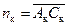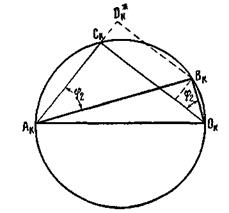
Рис. 2-25 Диаграмма для определения 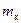и .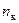

Непосредственное определение 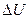из рис. 2-23 не может быть точным, так как отрезки 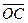, 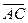во много раз меньше U_1н и 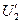. На основе рис. 2-25 может быть получена формула для 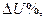рекомендованная ГОСТ на трансформаторы.

Из рис. 2-25 и равенств (2-56) имеем:

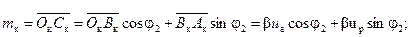(2-58)

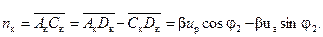(2-59)

Подставляя найденные значения m_к и n_к в (2-55), получим искомую формулу:

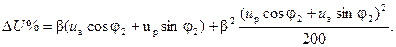(2-60)

При многих практических расчетах можно пренебречь вторым слагаемым, так как оно по сравнению с первым слагаемым незначительно.

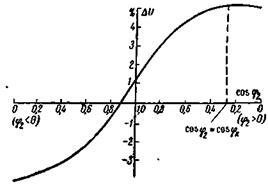
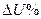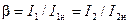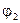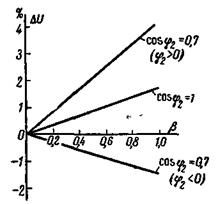
При помощи диаграммы, приведенной на рис. 2-25, или при помощи формулы (2-60) определяются важные в практическом отношении кривые, выражающие зависимости от от cos при 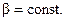Указанные кривые приведены на рис. 2-26 и 2-27.

Рис. 2-26. Кривые U% = f(b) при cosφ₂ = const. Рис. 2-27. Кривая U% = f(cosj₂) при b = const.

Здесь отрицательные значения 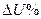при работе трансформатора с опережающим током соответствуют повышению напряжения при переходе от холостого хода к нагрузке (ср. с рис. 2-16).

Наибольшее значение 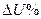получается при cos φ₂ = cos φ_к, что следует из рис. 2-23.

2-9. Потери и коэффициент полезного действия

При работе трансформатора в нем возникают потери — магнитные и электрические.

Магнитные потери, или потери в стали Р_с, принимаются, как отмечалось, равными потерям холостого хода P₀. Они зависят от частоты тока, от индукций В_с в стержне и В_я в ярме сердечника, а также от весов стержней и ярм. Для уменьшения магнитных потерь и реактивной составляю­щей тока холостого хода сечение ярма берут несколько больше (на 5—10%) сечения стержня. Потери P₀ приблизительно пропорциональны квадрату индукции (В²) и частоте тока в степени 1,3 (f^1,3).

Электрические потери, или потери короткого замыкания, пропорциональны квадрату тока.

Коэффициент полезного действия (к.п.д.) трансформатора имеет высокие значения: от 0,96 при S ≈ 5 кВА до 0,995 при номинальной мощности, составляющей десятки тысяч кВА. Поэтому определение его непосредственным методом по формуле

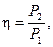(2-61)

где Р₂ — полезная (вторичная) мощность; Р₁ — затраченная (первичная) мощность, практически не может дать точных результатов.

Так как потери в трансформаторе невелики, то следует определять к.п.д. трансформатора косвенным методом и пользоваться при этом формулой

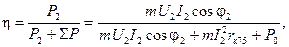(2-62)

где 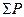— сумма всех потерь в трансформаторе;
m — число фаз;
r_к75 и P₀ — активное сопротивление короткого замыкания при 75°С и потери холостого хода, которые определяются, как указывалось ранее, по данным опытов короткого замыкания и холостого хода. Можно считать в обычных условиях U₂ = U_2н = const, 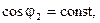P₀ = const.

Тогда, обозначив 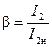, получим:

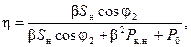(2-63)

где S_н = mU₂I_2н — номинальная мощность; Р_{к н} — потери короткого замыкания при номинальных токах в обмотках трансформатора.

В правой части (2-63) переменной величиной является только 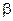. Обычным путем можно найти максимум функции 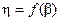. Для этого приравняем ее первую производную нулю:

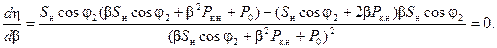
В полученной дроби знаменатель при реальных значениях 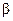не может быть равным бесконечности. Поэтому нужно приравнять нулю числитель. Отсюда найдем, что к.п.д. будет максимальным, когда потери короткого замыкания будут равны потерям холостого хода:

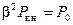, (2-64)

т. е. при равенстве переменных потерь постоянным потерям (при изменении нагрузки практически изменяются только потери короткого замыкания).

Для трансформаторов, выпускаемых заводами Советского Союза, имеем:

P₀ : P_к.н = 0,5÷0,25 ,что дает: 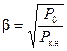= 0,7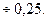

Следовательно, к.п.д. получается максимальным при нагрузке, составляющей 50—70% от номинальной. Такая нагрузка обычно и соответствует средней нагрузке при эксплуатации трансформатора.

При вычислении к.п.д. пользуются формулой

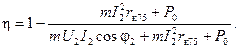(2-62,а)

2-10. Трансформирование трехфазного тока

Для трансформирования трехфазного тока применяются или трехфазные трансформаторы, или «трехфазные группы», состоящие из трех однофазных трансформаторов.

Наибольшее распространение на практике получили трехфазные стрежневые трансформаторы с расположением стержней в одной плоскости.

Сердечник одного из таких трансформаторов показан на рис. 2-28.

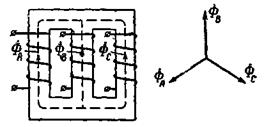
Рис. 2-28. Сердечник трехфазного стержневого трансформатора.

Здесь же указаны потоки (в соответствии с векторным уравнением потоков 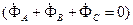, причем за положительное их направление условно принято направление снизу вверх. Очевидно, амплитуда потока в ярме равна амплитуде потока в стержне.

Трехфазная группа, состоящая из трех однофазных трансформаторов, представлена на рис. 2-29.

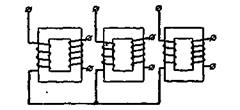
Рис. 2 29. Трехфазная группа.

Одна из ее обмоток соединена в звезду, другая, как правило, соединяется в треугольник (§ 2-13).

На рис. 2-30,а представлен трехфазный броневой трансформатор.

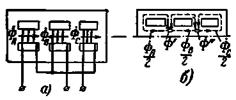
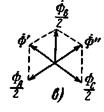
Рис. 2-30. Трехфазный броневой трансформатор и распределение потоков в его сердечнике.

Обычно его стержни располагаются горизонтально с помещенными на них дисковыми чередующимися обмотками (рис. 2-8). Здесь различают продольные ярма, расположенные параллельно стержням, и поперечные ярма, расположенные перпендикулярно стержням. Продольные и поперечные ярма выполняются обычно с сечением, равным примерно половине сечения стержня. В трехфазном броневом трансформаторе средняя фаза первичной и вторичной обмоток должна быть соединена в обратном порядке по сравнению с крайними фазами. На рис. 2-30,а показано соединение обмотки высшего напряжения в звезду. Здесь правый зажим средней фазы принят за начало фазы, а левый — за ее конец в противоположность тому, что принято для крайних фаз. Только в этом случае поток в промежуточных поперечных ярмах равен полусумме потоков соседних стержней (рис. 2-30,б и в).

Неправильным будет соединение, при котором за начало и конец средней фазы приняты такие же зажимы, что и для крайних фаз, так как в этом случае в промежуточных поперечных ярмах поток будет равен полуразности потоков в соседних стержнях, т. е. в 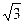раз больше, чем в предыдущем случае.

2-11. Соединения обмоток трансформаторов

Обратимся к однофазному трансформатору, обмотки которого показаны на рис. 2-31.

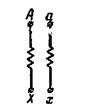
Рис. 2-31. Обозначения зажимов обмоток однофазного трансформатора.

Согласно ГОСТ зажимы обмоток обозначаются так, как указано на этом рисунке. Начало и конец обмотки высшего напряжения обозначаются соответственно прописными буквами А и X. Для обмотки низшего напряжения берутся строчные буквы: а — начало и х — конец обмотки.

Зажимы обмоток трехфазных трансформаторов обозначаются, как указано на рис. 2-32.

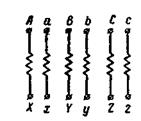
Рис. 2-32. Обозначения зажимов обмоток трех фазного трансформатора.

Зная обозначения зажимов обмоток, мы можем правильно соединить обмотки трехфазного трансформатора и трехфазной группы в звезду или треугольник. Их необходимо также знать при включении трансформаторов на параллельную, работу.

Соединение обмотки, например, высшего напряжения в звезду показано на рис. 2-33.

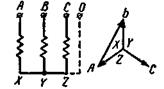
Рис. 2-33. Соединение обмотки в звезду.

Напомним, что в этом случае линейное напряжение в 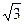раз больше фазного, а линейный ток равен фазному.

На рис. 2-34 показано соединение обмотки в треугольник.

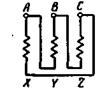
Рис. 2-34. Соединение обмотки в треугольник.

Здесь линейное напряжение равно фазному, а линейный ток в 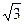раз больше фазного.

Соединение обмоток в звезду и звезду обозначают Y/Y и называют "звезда — звезда" или "игрек — игрек". Соединение обмоток в звезду и треугольник обозначают Y/D и называют "звезда — треугольник" или "игрек — дельта". Если от обмотки, соединенной в звезду, выводится нулевая точка, то такое соединение обозначают Y₀ и называют «звезда с нулем» или «игрек нулевое».

Следует иметь в виду, что отношение линейных напряжений U_л1 и U_л2 трансформатора зависит не только от чисел витков обмоток w₁ и w₂ (на фазу), но и от способов их соединения:

при Y/Y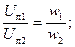

при Y/∆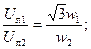

при ∆/Y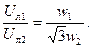

2-12. Группы соединений

В зависимости от сдвига по фазе между линейными первичной и вторичной э.д.с. на одноименных зажимах трансформаторы разделяются на группы соединений, причем каждую группу составляют трансформаторы с одинаковым сдвигом по фазе между указанными э.д.с.

Для обозначения группы соединений выбирается ряд целых чисел от 1 до 12; здесь условно принято, что единица соответствует 30° по аналогии с углами между минутной и часовой стрелками часов в 1, 2,..., 12 ч. При определении группы соединений с вектором э.д.с. обмотки высшего напряжения нужно совместить минутную стрелку, а с вектором э.д.с. обмотки низшего напряжения — часовую стрелку. Отсчет угла производится от минутной стрелки к часовой по направлению их вращения.

Обратимся к однофазному трансформатору, обмотки которого представлены на рис. 2-35.

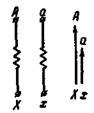
Рис. 2-35. Однофазный трансформатор 1/1-12.

Если они выполнены при одинаковом направлении намотки (например, по часовой стрелке, если смотреть от А к X и от a к х), то наведенные в них э.д.с. изобразятся векторами, направленными в одну и ту же сторону (рис. 2-35). Такой трансформатор принадлежит к группе соединений, обозначаемой числом 12. Его условное обозначение: 1/1-12.

Если тот же трансформатор будет иметь обмотку, например, низшего напряжения, у которой будут переставлены обозначения зажимов по сравнению с предыдущим случаем, то сдвиг между э.д.с. будет равен 180° (рис. 2-36).

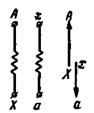
Рис. 2-36. Однофазный трансформатор 1/1-6.

Такой трансформатор принадлежит к группе соединений, обозначаемой числом 6.

Обратимся к трехфазному трансформатору, представленному на рис. 2-37.

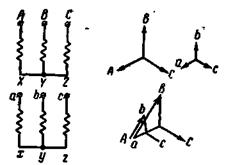
Рис. 2-37. Трехфазный трансформатор Y/Y-12.

Здесь обе обмотки соединены в звезду и намотаны в одинаковом направлении от начал к концам фаз. Векторные диаграммы э.д.с. показывают, что сдвиг между линейными э.д.с. АВ и ab в данном случае равен 0°. В этом мы убеждаемся, совместив при наложении диаграмм точки А и а. Следовательно, рассматриваемый трансформатор принадлежит к группе 12. Его полное обозначение: Y/Y-12.

Если у трехфазного трансформатора группы 12 поменять местами начала и концы фаз, например обмотки низшего напряжения, то получается трансформатор группы 6 (рис. 2-38). Его обозначают: Y/Y-6.

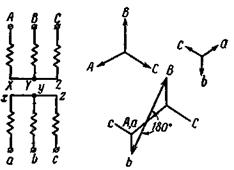
Рис. 2-38. Трехфазный трансформатор Y/Y-6.

Трехфазные трансформаторы с соединением обмоток Y/Y принадлежат к группам 6 и 12, если на каждом стержне сердечника помещены одноименные фазы. Если же у одной из обмоток сделать круговое перемещение обозначений зажимов, например вместо а—b—с сделать с—а—b и затем b—с—а, то при каждом перемещении будем поворачивать звезду вторичных э. д. с. на 120° и, следовательно, переходить от группы 12 к группам 4 и 8, а от группы b — к группам 10 и 2. Таким образом, при соединении обмоток Y/Y можем получить все четные группы соединений 2, 4, 6, 8, 10, 12.

Обратимся к трехфазному трансформатору с соединением обмоток Y/∆ представленному на рис. 2-39.

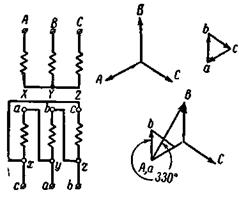
Рис. 2-39. Трехфазный трансформатор Y/∆-5.

Векторные диаграммы э.д.с., приведенные на этом же рисунке, показывают, что сдвиг между линейными э.д.с. здесь равен 330°. Следовательно, трансформатор принадлежит к группе 11. Он обозначается: Y/∆-11.

Если у рассмотренного трансформатора (рис. 2-39) поменять местами начала и концы фаз обмотки низшего напряжения, то получается трансформатор группы 5 (рис. 2-40) со сдвигом между линейными э.д.с., равным 150°. Такой трансформатор обозначается Y/∆-5.

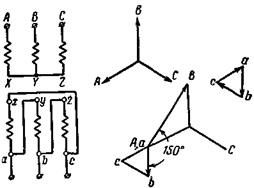
Рис. 2-40. Трехфазный трансформатор Y/∆-5.

Если сделать круговое перемещение обозначений зажимов для обмотки низшего напряжения трансформаторов, представленных на рис. 2-39 и 2-40, то перейдем соответственно от группы 11 к группам 3 и 7 и от группы 5 к группам 9 и 1. Следовательно, при соединении обмоток Y/∆ (или ∆/Y) можем noлучить все нечетные группы 1, 3, 5, 7, 9, 11.

Такое большое разнообразие групп соединений трансформаторов не только не требуется, но вызывало бы большие затруднения на практике, например при осуществлении параллельной работы трансформаторов (§ 2-17).

В СССР стандартизованы только две группы соединений: 12 и 11. Все выпускаемые советскими заводами нормальные однофазные трансформаторы и трехфазные с соединением обмоток Y/Y принадлежат к группе 12, а трехфазные трансформаторы с соединением обмоток Y/∆ — к группе 11.

2-13. Третьи гармоники в кривых тока холостого хода, магнитного потока и электродвижущих сил

Рассмотрим вначале процесс намагничивания однофазного трансформатора. Как отмечалось, вследствие нелинейной связи между потоком Ф в стальном сердечнике трансформатора и создающей его н.с. i₀w₁ кривая i₀ = f(t) отличается от синусоиды. Мы эту кривую найдем, пренебрегая потерями в стали и рассматривая вместо тока i_o намагничивающий ток i_μ, прак­тически равный i₀.

Кривую Ф = f(t) можно принять синусоидальной, если приложенное напряжение u₁ и, следовательно, уравновешивающая его э.д.с. е₁ — синусоидальные функции времени. В этом случае кривая i_μ = f(t) определяется графически, как показано на рис. 2-41.

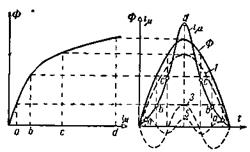
Рис. 2-41. Построение кривой намагничивающего тока i_μ = f(t) однофазного трансформатора при синусоидальном потоке.

Слева мы имеем кривую намагничивания Ф = f(i_μ) (здесь пренебрегаем гистерезисом). Справа для заданной синусоидальной кривой Ф = /(t) мы получаем кривую i_μ = f(t), ординаты которой a, b, с, d и т. д. равны абсциссам кривой Ф = f(i_μ) для соответствующих значений потока Ф.

Мы видим, что кривая тока искажена. Она имеет наряду с первой гармоникой довольно резко выраженные третью и пятую гармоники. Кривая тока построена для нормального трансформатора, имеющего, как это обычно бывает, максимальную индукцию в сердечнике около 14 500 Гс. В этом случае гармоники с номером выше пятого имеют небольшие значения.

Гистерезис мало искажает кривую тока. При разложении на гармоники кривой тока, построенной с учетом гистерезиса, мы получили бы, кроме синусоид, еще косинусоиды с малыми амплитудами. Они дают активную составляющую тока i_о, соответствующую потерям от гистерезиса.

При некоторых схемах соединения обмоток трехфазного трансформатора в кривой намагничивающего тока отсутствуют третья гармоника и гармоники с номером, кратным трем. Если принять кривую i_μ = f(t) синусоидальной, то кривая Ф = /(t) будет отличаться от синусоиды. Из высших гармоник в ней наиболее резко будет выражена 3-я гармоника. На рис. 2-42 приведено построение кривой Ф = /(t) при синусоидальной кривой i_μ = f(t).

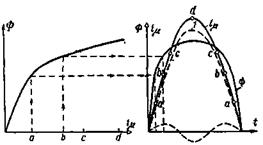Рис. 2-42. Построение кривой Ф = /(t) при синусоидальном намагничивающем токе.

Здесь по абсциссам а, b, с и т. д., равным ординатам кривой i_μ = f(t), найдены соответствующие значения потока Ф.

Обратимся к трехфазному трансформатору с соединением обмоток Y₀/Y. Будем считать, что с первичной стороны трансформатора выведена нулевая точка, которая соединена с нулевой точкой обмотки генератора трехфазного тока рис. 2-43.

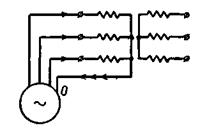
Рис. 2-43. Третьи гармоники намагничивающих токов трехфазного трансформатора при соединении обмоток Y₀/Y.

В этом случае намагничивающие токи фаз будут иметь третьи гармоники. Они совпадают по фазе и, следовательно, будут все направлены или oт генератора к трансформатору, или обратно. По нулевому проводу будет проходить ток, равный тройному значению третьей гармоники тока.

При отсутствии нулевого провода (при Y/Y) в кривых фазных намагничивающих токов третьи гармоники не могут иметь места, так как теперь для них нет замкнутого пути. Следовательно, в кривых фазных потоков появятся третьи гармоники, которые будут наводить в фазах обмотки третьи гармоники э.д.с.

Наиболее резко третьи гармоники будут проявляться в кривых фазных э.д.с. трехфазной группы и трехфазного броневого трансформатора. Здесь магнитное сопротивление для третьей гармоники потока мало, так как она проходит по стальному, сердечнику, как и первая гармоника; поэтому она может достичь относительно больших значений: при обычных насыщениях сердечником указанных трансформаторов амплитуда третьей гармоники фазной э.д.с. достигает 40—50% амплитуды первой гармоники той же э.д.с.

В трехфазном стержневом трансформаторе при соединении обмоток Y/Y в кривых фазных э.д.с. также будут иметь место третьи гармоники. Однако здесь вследствие большого магнитного сопротивления для третьих гармоник потоков фаз они относительно малы: их амплитуда обычно не пре­вышает 5—7% амплитуды первой гармоники фазной э.д.с. Увеличение магнитного сопротивления для третьих гармоник фазных потоков объясняется тем, что они в любой момент времени будут направлены по стержням трансформатора или вверх, или вниз и не могут, следовательно, замыкаться по стальному сердечнику, а принуждены часть пути проходить по воздуху или маслу, как показано на рис. 2-44.

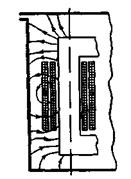
Рис. 2-44. Приближенная картина поля, соответствующего третьим гармоникам фазных потоков.

Из рис. 2-44 также следует, что наличие третьих гармоник в фазных потоках трехфазного стержневого трансформатора несколько повышает потери в стали (в стенках бака, конструктивных деталях трансформатора).

Наличие третьих гармоник в фазных э.д.с. не нарушает необходимого условия работы трансформатора — равновесия приложенного напряжения и наведенной в обмотке э.д.с. Действительно, хотя фазная э.д.с. будет иметь третью гармонику, но междуфазная э.д.с. ее иметь не будет, так как при соединении обмотки звездой третьи гармоники фазных э.д.с. при обходе двух фаз, встречно соединенных, направлены друг против друга.

Если одна из обмоток трехфазного трансформатора соединена треугольником, то третьи гармоники в кривых потоков, а следовательно, и фазных э.д.с. практически пропадают. Это объясняется тем, что в обмотке, соединенной треугольником, третьи гармоники фазных э.д.с. направлены по контуру в одну сторону; они создадут третью гармонику тока, при наличии которой поток становится почти синусоидальным.

Теперь должно быть ясным, почему обмотки трехфазной группы и трехфазного броневого трансформатора выполняются, как правило, с соединением Y/D или ∆/Y. Обмотки трехфазного стержневого трансформатора часто имеют соединение Y/Y. Однако и здесь при большой мощности (больше 1800 кВА) выбирается соединение Y/∆ или ∆/Y.

Ранее иногда, в случае необходимости иметь соединение обеих обмоток мощного трехфазного трансформатора в звезду, снабжали такой трансформатор третьей обмоткой, соединенной треугольником, причем никаких выводов от этой обмотки не делалось, она служила только для компенсации третьей гармоники в кривой фазной э.д.с. Такую обмотку будем называть компенсационной. В настоящее время она используется как третья рабочая обмотка (см. § 2-16).

2-14. Расчет тока холостого хода

Ток холостого хода I_о имеет активную составляющую I_оа и реактивную составляющую I_ор

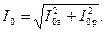
Активная составляющая тока холостого хода, как указывалось, зависит от потерь Р_с в стали сердечника:

для однофазного трансформатора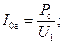

для трехфазного трансформатора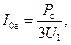

где U₁ — фазное напряжение.

В действительности потери в стали зависят от потока Ф_м и, следовательно, от э.д.с. Е₁; однако практически при определении потерь Р_с можно считать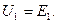

Потери в стали сердечника зависят от: В_с ─ индукции в стержнях, Гс; В_а ─ в ярмах, Гс; веса G_я ─ стержней и Gя ─ ярм, кг; f ─ частоты перемагничивания, Гц. Приближенно можно принять:

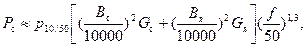Вт, (2-65)

где p_10/50 — удельные потери в листовой стали, Вт/кг, из которой выполнен сердечник трансформатора, при максимальной индукции 10000 Гс и частоте 50 Гц.

Для силовых трансформаторов обычно выбирается сталь марок Э41, Э42 и холоднокатаная Э320 (при толщине листа ∆ = 0,5 или 0,35 мм); для указанных марок стали р_10/50 соответственно равняется 1,6; 1,4 и 1,15 — 1,20 Вт/кг (при ∆ =0,5 мм) и 1,35; 1,2; 0,9—0,95 Вт/кг (при ∆ = 0,35 мм).

Значения индукций определяются по формулам

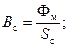
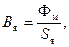
где S_c и S_я — площади сечения стержня и ярма, см² (берется площадь без изоляции между листами); значение Ф_м , мкс, рассчитывается по уравнению

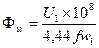. (2-66)

Веса G_c и G_я определяются по геометрическим размерам и удельному весу для листовой стали γ_с = 7,6 кг/дм³.

Из (2-65) следует, что при увеличении частоты f сверх номинальной и при сохранении неизменным номинального первичного напряжения потери Р_с будут уменьшаться, так как при этом согласно (2-66) поток Ф_м, а следовательно, и В изменяются обратно пропорционально f.

Реактивная составляющая тока холостого хода I_0р определяется из расчета магнитной цепи трансформатора следующим образом.

На рис. 2-45,а представлен сердечник однофазного трансформатора.

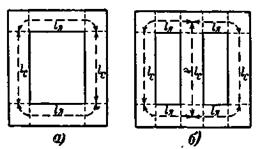
Рис. 2-45. Эскизы магнитных цепей.
а—однофазного трансформатора (п_в = 4); б—трехфазного трансформатора (для крайних фаз п_в = 3; для средней n_в=1).

Здесь жирным пунктиром показан путь главного потока Ф. Согласно закону полного тока н.с. 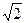I_0рw₁, необходимая для создания в сердечнике потока Ф_м, определяется из уравнения
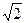I_0рw₁ = 2H_cl_c + 2H_яl_я + 0,8B_cn_вδ_в, (2-67)
где H_с и Н_я — напряженности поля в стержне и ярме, А/см, которые определяются по кривым намагничивания (рис. 2-46) соответственно для индукций В_с и В_я;
n_в — число зазоров, которое принимается равным четырем для однофазного трансформатора при сборке его сердечника «внахлестку»;
δ_в ≈ 0,0035 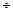0,005 см — зазор при той же сборке сердечника.

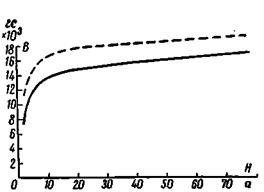
Рис. 2-46. Кривые намагничивания трансформаторной листовой стали: сплошная — для Э41 и Э42; пунктирная — для Э320.

Из (2-67) реактивная составляющая тока холостого хода, А:

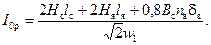(2-68)

На рис. 2-45,б представлен сердечник трехфазного стержневого трансформатора. При расчете I_0р такого трансформатора сначала определяется I_0р(кр) для крайних фаз по формуле

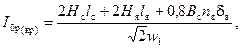
где n_в = 3; затем для средней фазы по формуле

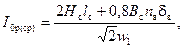
где n_в = 1. Ток I_0р принимается равным среднему арифметическому:

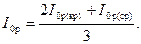
При расчете I_0р мы пренебрегаем высшими гармониками тока i_0р 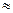i_μ, так как они при обычных значениях индукций мало влияют на действующее значение I_0р.

Из кривых намагничивания рис. 2-46 мы видим, как сильно влияет насыщение стали (значение В) на Н, а следовательно, и на I_0р. Обычно при стали Э41 и Э42 значения B_с = 10000 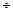14500 Гс и при стали Э320 В_с = 13000 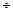16500 Гс, В_я = (0,90 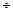0,95) В_с для масляных трансформаторов мощностью от 5 до 100000 кВА; для сухих трансформаторов они снижаются на 10 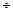20%. При таких индукциях ток I_0р (I_0р 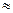I₀) составляет от 10 до 4% номинального тока I_1н.

2-15. Определение параметров трансформатора расчетным путем

Расчет активных сопротивлений r_j и r_2, Ом, может быть произведен, если известны сечения проводников обмоток s₁ и s₂, мм², число витков w_l и w₂ и средние длины витков l_ср1 и l_ср2, м. Тогда имеем:

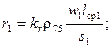
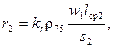
где k_r = 1,03 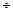1,05 — коэффициент, учитывающий потери, вызванные полями рассеяния обмоток;

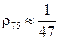— удельное сопротивление меди при 75° С;

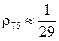— тоже для алюминия.

Активное сопротивление короткого замыкания

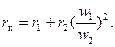
Потери в обмотках при номинальных токах (сюда же относятся и потери, вызванные полями рассеяния), Вт

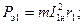
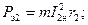
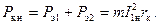
Формулы для потерь можно преобразовать следующим образом:

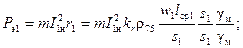
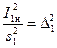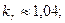
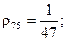
подставив ─ квадрат плотности тока первичной обмотки, А/мм²; 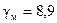─ удельный вес меди; 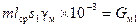─ вес меди первичной обмотки, кг, получим:

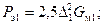(2-69)

аналогично будем иметь.

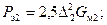(2-70)

при алюминиевых обмотках (γ_а 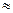2,65)

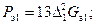
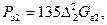
где G_al и G_a2 — веса обмоток, кг.

Расчет индуктивных сопротивлений рассеяния х₁ и х₂ может быть произведен только приближенно, так как не представляется возможным точно установить распределение поля рассеяния. Мы рассмотрим метод расчета х₁ и х₂ для цилиндрических обмоток. Они в разрезе с одной стороны стержня показаны на рис. 2-47. Здесь же показана часть стержня, на котором помещены обмотки.

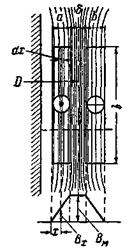
Рис. 2-47. К расчету х_к = х₁ + х'₂ (см. рис. 2-13).

Мы считаем, что поле рассеяния создается н.с. i₁w₁ и равной ей н.с. i₂w₂ = 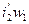(пренебрегаем при этом н.с. i₀w₁) и что индукционные линии этого поля направлены, как показано на рис. 2-47, параллельно стенкам обмоток, равным по высоте. Примем, что магнитные сопротивления индукционных трубок поля обусловлены только их частью вдоль обмоток и промежутка между ними. Магнитным сопротивлением остальных частей индукционных трубок пренебрегаем. Кривая н.с., создающей поле рассеяния, в этом случае изобразится трапецией, а так как μ для воздуха (или масла), меди и изоляции — величина постоянная, то кривая распределения индукции вдоль пунктирной линии также изобразится трапецией.

Найдем индуктивность рассеяния первичной обмотки:

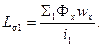
Будем условно считать, что потокосцепление, определяющее L_σ1 создается индукционными линиями, находящимися слева от штрихпунктирной линии, разделяющей промежуток δ пополам. Оно рассчитывается следующим образом.

Поток в промежутке 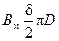сцепляется со всеми w₁ витками (здесь для определения площади, через которую проходит поток, нужно было бы взять средний диаметр 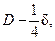а не D, но в дальнейшем при определении потока промежутка, сцепляющегося со вторичной обмоткой, мы возьмем также D, а не 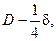что до некоторой степени компенсирует допущенную ошибку). Индукционные линии, проходящие вдоль обмотки, дают различные сцепления с витками обмотки. Поток в стенке цилиндра с толщиной dx равен B_xdxπD (здесь также приближенно взят постоянный диаметр D), где 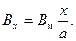Он сцепляется с 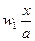витками. Следовательно, полное потокосцепление первичной обмотки

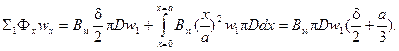(2-71)

Аналогично определяется потокосцепление 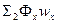вторичной обмотки, от которого зависит индуктивность рассеяния L_σ2:

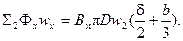(2-72)

Индукция в промежутке между обмотками, В·с/см²,