Безразмерная величина

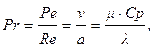(2.13)

где µ - коэффициент динамической вязкости жидкости, представляет собой новый критерий, называемый критерием Прандтля. Критерий Прандтля целиком составлен из физических параметров, а поэтому и сам является физическим параметром.

Полученные критерии (числа) можно разделить на два вида:

определяемые критерии – это критерии, в которые входят искомые зависимые переменные; в рассматриваемом случае зависимыми переменными являются a, J, W_x, W_y, W_z и Р, следовательно, определяемыми являются критерии Nu,q, W_x, W_y, W_z и Eu;

определяющие критерии – это критерии, которые целиком составлены из независимых переменных или постоянных величин, входящих в условия однозначности; в рассматриваемом случае определяющими являются критерии X, Y, Z, Re, Pe(Pr) и Gr. В зависимости от условий задачи определяющие критерии могут стать определяемыми, и наоборот.

Условия подобия физических процессов можно сформулировать в виде трех правил:

1. Подобные процессы должны быть качественно одинаковыми, т.е. иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями.

2. Условия однозначности подобных процессов должны быть одинаковыми во всем, кроме численных значений постоянных, содержащихся в этих условиях.

3. Одинаковые определяющие критерии подобных процессов должны иметь одинаковую численную величину.

Первое условие говорит, что подобные процессы должны относиться к одному и тому же классу физических явлений. Помимо одинаковой физической природы, подобные процессы должны характеризоваться одинаковыми дифференциальными уравнениями.

Второе условие подобия требует, чтобы условия однозначности подобных процессов были одинаковыми во всем, кроме численных значений постоянных, содержащихся в этих условиях, т.е. подобные процессы должны принадлежать к одной и той же группе явлений.

Первых двух условий недостаточно для установления физического подобия. Нужно добавить условие, что одноименные определяющие критерии подобных процессов должны иметь одинаковую численную величину.

Три условия подобия составляют содержание теоремы Кирпичева-Гухмана.

2.1.2 Теплоотдача при вынужденном продольном обтекании плоской
поверхности

Будем полагать, что плоская поверхность омывается потоком жидкости, скорость и температура которого вдали от твердого тела постоянны и равны соответственно W₀ и t₀. Поток направлен вдоль стенки.

Около стенки образуется гидродинамический пограничный слой. В пределах слоя скорость жидкости изменяется от нуля до скорости невозмущенного потока.

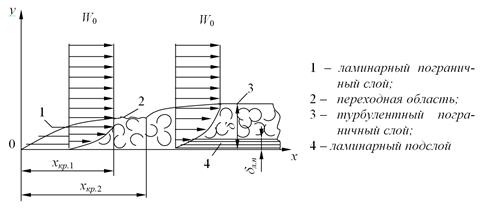
Рисунок 2.2 - Схема пограничного слоя

Течение в пограничном слое будет ламинарным и турбулентным. Однако и при турбулентном слое у стенки образуется весьма тонкий слой жидкости, называемый ламинарным или вязким подслоем, в котором течение подчиняется закономерностям ламинарного движения.

Опыт показывает, что переход из ламинарной формы течения в турбулентную происходит не в точке, а на некотором участке. Течение на этом участке имеет нестабильный характер и называется переходным.

О режиме течения в пограничном слое судят по критической величине критерия Рейнольдса:

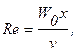
где х – продольная координата, отсчитываемая от передней кромки.

Согласно /14/ переход ламинарного режима в турбулентный происходит при Re =1×10⁴¸4×10⁶.

При наличии теплообмена, кроме гидродинамического, образуется также и тепловой пограничный слой. В пределах теплового слоя температура жидкости изменяется от значения, равного температуре поверхности стенки t_W , до значения, равного температуре жидкости вдали от пластины t₀.

Определяющими параметрами процесса конвективного теплообмена являются определяющий размер и определяющая температура.

За определяющий размер принимают тот размер, от которого процесс теплообмена зависит в большей степени и который в большей степени отвечает физическому существу процесса.

За определяющую температуру принимают ту температуру, при которой проводят вычисления физических параметров, составляющих критерии подобия.

Для расчета теплоотдачи при ламинарном режиме

(где ℓ₀ – длина пластины) могут быть рекомендованы следующие формулы:

для локальной теплоотдачи (формула (3-9) /27/):

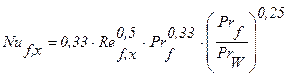; (2.15)

для средней теплоотдачи (формула (3-10) /27/):

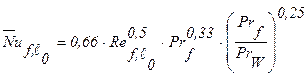. (2.16)

Здесь за определяющую температуру принята температура набегающей на тело жидкости t₀, что отмечено индексом f (исключение составляет величина Pr_W, выбираемая по температуре стенки). За определяющие размеры берутся величины x, ℓ₀, отсчитываемые от начала пластины.

Для расчета теплоотдачи при турбулентном режиме (Re_f,ℓ0³4×10⁶) рекомендуются формулы:

для локальной теплоотдачи (формулы (7-35)/14/, (3-11) /27/):

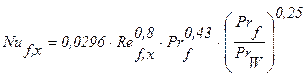; (2.17)

для средней теплоотдачи (формула (3-12), /27/):

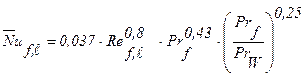. (2.18)

2.1.3 Теплоотдача при вынужденном течении жидкости в трубах

Течение жидкости в трубах может быть ламинарным и турбулентным. О режиме течения судят по величине критерия:

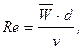(2.19)

где 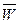– средняя скорость жидкости, d – внутренний диаметр трубы.

Если Re<Re_кр.1»2000, то течение является ламинарным. Развитое турбулентное течение в технических трубах устанавливается при Re>Re_кр.2»10⁴. Течение при Re»2×10³¸10⁴ называется переходным. Ему соответствует и переходный режим теплоотдачи.

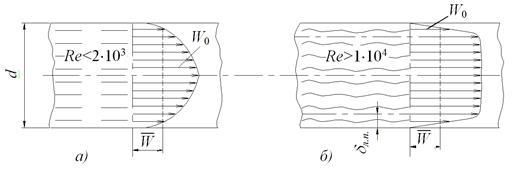
Рисунок 2.3 - Распределение скорости по сечению при ламинарном (а) и турбулентном (б) режимах изотермического течения жидкости в трубах

При ламинарном течении жидкости, Re_f,d < 2×10³, для определения среднего коэффициента теплоотдачи рекомендуется следующая расчетная формула (формула (3-33) /27/):

(2.20)

При развитом турбулентном режиме , Re_f > 10⁴, расчетная формула имеет следующий вид (формула (3-28) /27/)

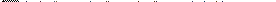(2.21)

В качестве определяющих величин были приняты: диаметр трубы d, определяющая температура t_f, средняя скорость жидкости W.

Для воздуха эти формулы упрощаются и принимают следующий:

; (2.22)

. (2.23)

Приведенные формулы (2.20) – (2.23) применимы к трубам любой формы поперечного сечения – круглого, квадратного, прямоугольного, треугольного, кольцевого (d₂/d₁=1¸5,6), щелевого(a/b=1¸40, a и b – размеры щели), а также для продольно омываемых пучков труб при 1/d_эк>50.

В этих случаях за определяющий размер надо принимать эквивалентный диаметр d_эк, равный учетверенной площади поперечного селения канала, деленной на его полный (смоченный) периметр, независимо от того, какая часть этого периметра участвует в теплообмене. Для круглых труб эквивалентный диаметр равен геометрическому.

При 1/d< 50 значение коэффициента теплоотдачи выше, поэтому полученное значение a умножается еще на поправочный коэффициент e_e>1(таблицы 8-1, 8-2 /14/).

2.1.4 Теплоотдача при поперечном омывании одиночной трубы

Омывание трубы поперечным потоком жидкости характеризуется рядом особенностей. Плавное безотрывное обтекание цилиндра, которое имеет место при 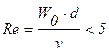(W₀ – скорость набегающего потока, d– внешний диаметр), при Re >5 меняется.

Пограничный слой, образующийся на передней половине трубы, в корневой части отрывается от ее поверхности, и позади цилиндра образуются два симметричных вихря.

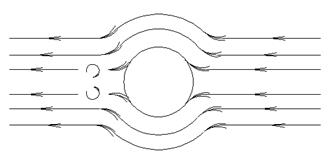
Рисунок 2.4 - Омывание цилиндра с отрывом от пограничного слоя

При дальнейшем увеличении критерия Рейнольдса вихри вытягиваются по течению все дальше и дальше от цилиндра. При Re³10³ вихри периодически отрываются от трубы и уносятся потоком жидкости, образуя за цилиндром вихревую дорожку.

При обработке и обобщении опытных данных по теплоотдаче при поперечном обтекании труб в качестве определяющих принимаются следующие величины: скорость W₀, температура t_f набегающего потока и диаметр трубы d.

Для одиночного цилиндра расчетные формулы для определения среднего по окружности цилиндра коэффициента теплоотдачи имеют следующий вид:

При Re_f = 5¸1×10³ (формула 9-1 /14/):

. (2.24)

При Re_f =1×10³ ¸ 2×10⁵ (формула 9-2 /14/):

. (2.25)

Формулы (2.24) и (2.25) справедливы для любых жидкостей. Для воздуха эти закономерности упрощаются и принимают вид:

; (2.26)

(2.27)

2.1.5 Теплоотдача при свободном движении жидкости

Свободное движение возникает за счет изменения в рассматриваемой жидкости массовых (объемных) сил. Такими силами являются сила тяжести, центробежная сила и силы за счет наведения в жидкости электромагнитного поля высокой напряженности.

В уравнении движения (2.4а) гравитационные силы учитываются членом rgJ. Произведение rg имеет размерность силы, отнесенной к единице объема. При теплообмене температура жидкости переменна. Вследствие этого возникает разность плотностей и, как следствие, разность гравитационных сил, представляющих собой подъемную силу.

Рассмотрим теплоотдачу при свободном гравитационном движении.

При рассмотрении теплоотдачи при свободном движении жидкости в большом объеме предполагается, что объем жидкости настолько велик, что свободное движение, возникающее у других тел, расположенных в этом объеме, не сказывается на рассматриваемом течении. Как и при вынужденной конвенции, свободное движение жидкости может быть как ламинарным, так и турбулентным.

2.1.5.1 Теплопередача при свободном ламинарном движении вдоль вертикальной пластины

Пусть вертикальная пластина с неизменной температурой поверхности t_W, находится в жидкости или газе. Жидкость вдали от пластины неподвижна (вынужденное течение отсутствует), температура жидкости вдали от пластины постоянна и равна t₀. Примем, что t_W> t₀. При этом у пластины появляется подъемное движение нагретого слоя жидкости. Вдали от пластины скорость по- прежнему равна нулю.

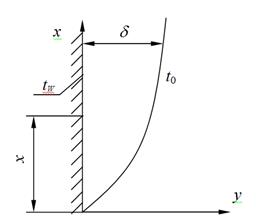
Рисунок 2.5 - К выводу формулы для коэффициента теплоотдачи при свободной конвенции. δ - толщина движущегося слоя жидкости.

Толщина движущегося слоя жидкости переменна по высоте и связана со скоростью движения в этом слое.

Текущее значение критерия Нуссельта аналитически получено в виде:

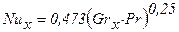, (2.28)

где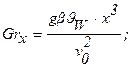

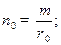
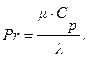
Здесь 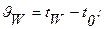b - коэффициент объемного расширения жидкости;

m - коэффициент динамической вязкости,

λ – коэффициент теплопроводности,

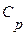- удельная теплоемкость жидкости в движущемся слое.

Средняя теплоотдача вертикальной пластины при t_W=const в ламинарном течении:

. (2.29)

Произведение критериев Gr_ℓ∙Pr часто называют критерием Рэлея и обозначают Ra.

Для расчета местных коэффициентов теплоотдачи при свободном ламинарном течении вдоль вертикальных стенок можно использовать формулу:

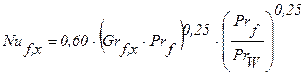. (2.30)

Здесь определяющей является температура жидкости за пределами движущегося слоя. Pr_W выбирается по местной температуре стенки. Определяющий размер – продольная вдоль потока координата, отсчитываемая от места начала теплообмена. Формула (2.30) получена при условии, что q_W=const.

Расчетная формула для средних коэффициентов теплоотдачи:

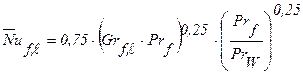. (2.31)

Здесь определяющей температурой по-прежнему является температура жидкости за пределами движущегося слоя, определяющий размер – длина пластины, отсчитываемая от начала теплообмена. Формула (2.31) получена для теплоносителей с числами Прандтля 0,7-3×10³. Ею следует пользоваться при 10³ <Gr_f,x×Pr_f <10⁹.

2.1.5.2 Теплоотдача при свободном турбулентном движении вдоль вертикальной пластины

Развитое турбулентное течение наступает при числах Gr_f,x×Pr_f ³ 6×10¹⁰.

Для местных коэффициентов теплоотдачи предложена формула:

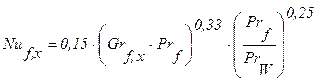. (2.32)

Определяющие температура и линейный размер выбраны так же, как и в формуле (2.31).

Линейный размер входит в критерии Nu и Gr:

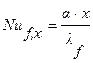и .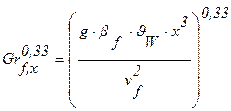

Отсюда следует, что при развитом турбулентном течении коэффициент теплоотдачи не зависит от линейного размера и, следовательно, местный коэффициент теплоотдачи равен среднему:

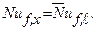
Описанная картина свободного движения вдоль вертикальной стенки типична также и для свободного движения у наклонной стенки, шаров, горизонтальных круглых и овальных труб.

2.1.6 Теплоотдача жидких металлов

Расплавленные металлы применяют в тех случаях, когда необходимо обеспечить интенсивный отвод тепла от поверхности нагрева или когда при низком давлении требуется иметь высокую температуру рабочей жидкости. Наиболее приемлемыми теплоносителями являются щелочные и тяжелые металлы и их сплавы: натрий, калий, натриево-калиевый сплав, литий, висмут, ртуть и т.д. Физические свойства жидких металлов существенно отличаются от свойств обычных теплоносителей – воды, масла и т.д. У металлов больше плотность и коэффициент теплопроводности; значение же теплоемкости ниже, особенно мала величина критерия Прандтля (Pr» 0,005 – 0,05). Кроме того, у тяжелых и щелочных металлов физические параметры слабо зависят от температуры.

Для расчета теплоотдачи при турбулентном течении (Re_d >2000) в прямой круглой трубе для гидродинамически и термически стабилизированного течения и q_W= const в характерном для жидких металлов интервале чисел в /14/ рекомендуется формула:

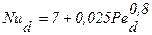, (2.33)

где 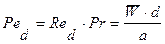– число Пекле.

При q_W =const критерий Nu_d в области стабилизированного ламинарного течения не зависит от Pe_d и равен постоянному значению:

Nu_d = 4,36. (2.34)

2.1.7 Теплоотдача при течении газа с большими скоростями

При течении газа с большими скоростями гидродинамические и тепловые процессы непрерывно связаны. Течение характеризуется взаимным преобразованием внутренней и кинетической энергии потока и расширением газа. Для характеристики газовых потоков скорость их движения сопоставляется со скоростью распространения звука в этой среде. Это отношение обозначают буквой М и называют числом Маха. Если М <1, то поток называется дозвуковым, если М =1 – звуковым и если М >1 – сверхзвуковым.

В реальных условиях частицы газа, непосредственно прилегающие к поверхности теплоизолированного тела, будут иметь температуру, превышающую температуру газа вдали от тела. Эта температура называется собственной, адиабатической или равновесной. Собственная температура (иногда ее называют также температурой восстановления) определяется из уравнения:

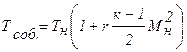, (2.35)

где Т – температура незаторможенного потока (термодинамическая температура);
к – показатель адиабаты ( 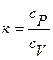– соотношение удельных теплоемкостей при постоянных давлении и объеме); М_н – число Маха набегающего потока.

Для продольно обтекаемой пластины при ламинарном течении 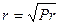, при турбулентном течении .

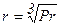Уравнение теплоотдачи при течении газа с большими скоростями принимает вид (формула (11-32) /14/):

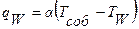, (2.36)

где α – коэффициент теплоотдачи

Местные коэффициенты теплоотдачи при продольном омывании пластины турбулентным пограничным слоем рассчитываются по формуле (формула (11-34) /14/):

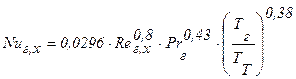. (2.37)

Здесь Т_г – температура газа вдали от стенки, Т_Т – температура торможения.

Для ламинарного пограничного слоя может быть рекомендовано выражение (формула (11-35) /14/):

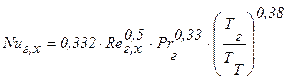. (2.38)

В формулах (2.37), (2.38) в качестве определяющей температуры при определении коэффициентов теплоотдачи используется значение температуры Т_г.

Температура торможения равна

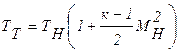. (2.39)

Поэтому 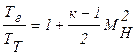. (2.40)

В случае движения тела со сверхзвуковой скоростью (W_Н>a_Н) перед ним возникает ударная волна (скачок уплотнения). W_Н, a_Н – соответственно, скорости набегающего потока и скорость звука перед скачком уплотнения.

В случае, когда фронт волны составляет прямой угол с направлением распространения, волна называется прямой ударной волной, или прямым скачком уплотнения. Скачки уплотнения удобно наблюдать в сверхзвуковых аэродинамических трубах при обтекании воздухом неподвижных твердых тел.

Остановив ударную волну встречным потоком газа, получим некоторую неподвижную поверхность, пересекая которую все элементарные струйки газа одновременно претерпевают скачкообразные изменения скорости движения, плотности, давления и температуры (рисунок 2.6).

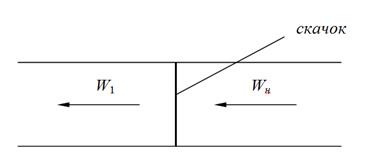
Рисунок 2.6 - Скачок уплотнения

В прямом скачке уплотнения всегда сверхзвуковая скорость газа переходит в дозвуковую.

Косой скачек получается в том случае, когда, пересекая фронт скачка, газовый поток должен изменить свое направление (рисунок 2.7). Например, при сверхзвуковом обтекании газом клиновидного тела, которое отклоняет поток от начального направления на угол w, перед телом образуются косые скачки уплотнения. Если до встречи струи с фронтом косого скачка вектор скорости W_н составляет с ним угол a, то после пересечения фронта струя отклоняется на угол w, а угол между вектором скорости и фронтом скачка становится равным

b = a - w.

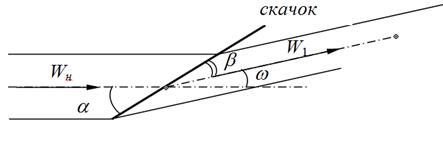
Рисунок 2.7 - Схема косого скачка уплотнения

2.1.8 Элементы расчета теплообменников

Теплообменники – это устройства, в которых тепло переходит от одной среды к другой.

Рекуперативные теплообменные аппараты представляют собой устройства, в которых две жидкости с различными температурами текут в пространстве, разделенном твердой стенкой.

Если тепло Q первого (горячего) теплоносителя воспринимается вторичным (холодным), то уравнение теплового баланса без учета потерь тепла запишется в виде:

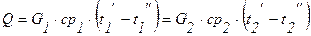. (2.41)

Здесь G – расход массы, кг/с; C_р – средняя теплоемкость, 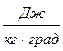; t – температура теплоносителя, С°. Индекс 1 означает, что данная величина отнесена к горячей жидкости, 2 – к холодной. Обозначение (¢) соответствует данной величине на входе в теплообменник, (²) – на выходе.

Величину С = G×С_p, Вт/град называют водяным эквивалентом.

Из уравнения (2.41) следует, что

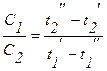. (2.42)

Тогда

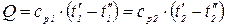. (2.43)

Характер изменения температур теплоносителей вдоль поверхности будет определяться схемой движения и водяными эквивалентами.

Уравнение теплопередачи служит чаще всего для определения поверхности теплообмена F и может быть записано в виде:

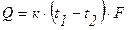, (2.44)

где к – коэффициент теплопередачи, t₁ и t₂ – соответственно средние температуры первичного и вторичного теплоносителей.

Для определения средней разности температур теплоносителей на участке поверхности F воспользуемся соотношением

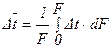, (2.45)

где Dt – местное значение температурного напора (t₁-t₂), относящееся к элементу поверхности теплообмена.

Если усреднение температурного напора проводится по всей поверхности теплообмена, то

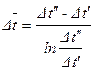, (2.46)

где Dt² = t₁² - t₂²; Dt¢ = t₁¢ - t₂¢.

Полученная средняя разность температур называется среднелогарифмическим температурным напором. Формула (2.46) справедлива для простейших схем теплообменников (прямоток, противоток) при условии постоянства массового расхода теплоносителей и коэффициента теплоотдачи вдоль всей поверхности теплообмена.

В этом случае уравнение (2.44) может быть записано в виде:

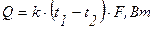. (2.47)