Примеры решения задач. Определить средний коэффициент теплоотдачи a и полную теплоотдачу для плоской пластины шириной b = 0,5 м и длиной l = 0,72 м
Задача 2.1
Определить средний коэффициент теплоотдачи a и полную теплоотдачу для плоской пластины шириной b = 0,5 м и длиной l = 0,72 м. обдуваемой воздухом со скоростью W = 30 м/с, если температура пластины tW = 100°С и температура воздуха tf = 20°С. Параметры воздуха при температуре 20°С:
коэффициент температуропроводности af = 21,4×10-6 м2/с;
коэффициент теплопроводности lf = 0,0261 Вт/м×град;
коэффициент кинематической вязкости nf = 15,06×10-6 м2/с.
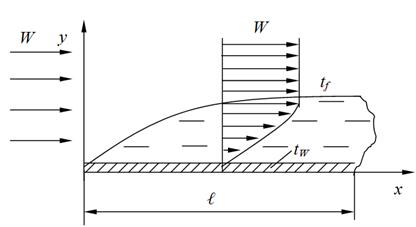
Рисунок 2.8
Решение
Определяем значение критерия Рейнольдса для пластины при х = ℓ (индекс «f» означает, что в качестве определяющей температуры берется температура набегающего потока, т.е. tf =20°С):
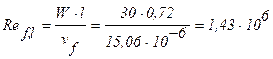 .
.
Значение критерия Ref =1,43×106, соответствует значению критерия Ref=4×106в режиме перехода ламинарного течения в турбулентное.
Считая, что на пластине развивается режим турбулентного движения, будем иметь (формула 2.18):
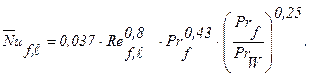
Значение критерия Прандтля для воздуха при температуре 20°С:
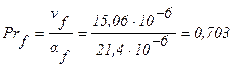 .
.
Параметры воздуха при температуре 100°С:
коэффициент температуропроводности aW=33,64×10-6 м2/с;
коэффициент кинематической вязкости nW=23,13×10-6 м2/с.
Значение критерия Прандтля для воздуха при температуре 100°С:
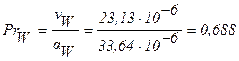 .
.
Тогда:
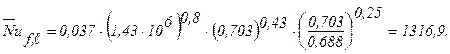
Коэффициент теплоотдачи будет равен:
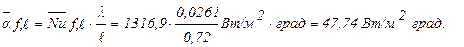
Полная теплоотдача будет равна:
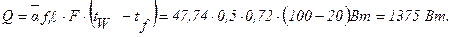
Задача 2.2
Тонкая пластина длиной ℓ0 =2 м и шириной b=1,5 м обтекается продольным потоком со скоростью W0=0,1 м/с и температурой t0=20°С. Температура поверхности пластины tW =160°С. Определить средний по длине коэффициент теплоотдачи и количество тепла, отдаваемое пластиной воздуху.
Вычислить толщину гидродинамического пограничного слоя и значения местных коэффициентов теплоотдачи на различных расстояниях от передней кромки пластины х=0,1ℓ0; 0,2ℓ0; 0,5ℓ0; ℓ0. Построить график зависимости толщины гидродинамического слоя и коэффициента теплоотдачи от относительного расстояния х/ℓ0.
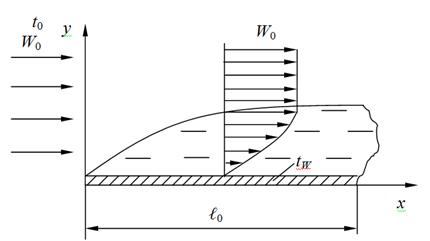
Рисунок 2.9
Решение
Параметры воздуха при температурах 120; 160°C определяем по таблице
П-3 /27/.
Определим значение критерия Рейнольдса для пластины:
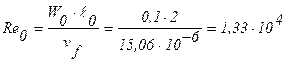
Критические значения критерия Рейнольдса при переходе от ламинарного потока к турбулентному составляют 1×104 - 4×106.
Принимаем, что пограничный слой на пластине ламинарный.
Критерий Прандтля будет равен:
при температуре tf =20°C:
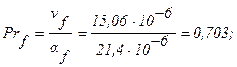
при температуре tf =160°C:
 .
.
Среднее значение числа Nuf,ℓ0 для пластины длиной ℓ0 будет равно (формула 2.16):
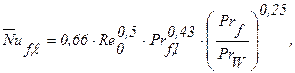
где 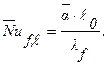
Тогда:
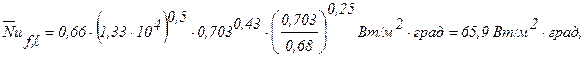
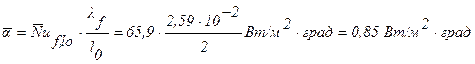
Количество передаваемого тепла с обеих сторон пластины
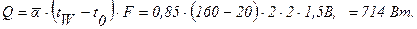
Толщина ламинарного пограничного слоя dл и коэффициент теплоотдачи aх на расстоянии х от передней кромки пластины определяются выражениями:
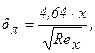 (формула 7-10 /14/),
(формула 7-10 /14/),
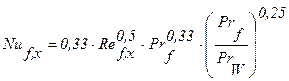 (формула 7-5¢ /14/),
(формула 7-5¢ /14/),
где 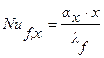 ;
; 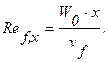
На расстоянии х = 0,1ℓ0
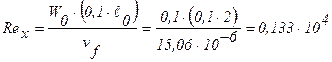 ;
;

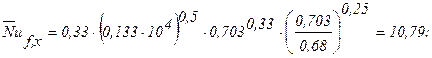
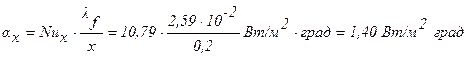 .
.
Результаты расчетов dл и aх в зависимости от относительного расстояния х/ℓ0 приведены в таблице:
| х/ℓ0 | 0,1 | 0,2 | 0,5 | 1,0 |
| dl×103, м | 26,5 | |||
| aх, Вт/м2×град | 1,40 | 0,99 | 0,63 | 0,44 |

Рисунок 2.10 – График функции dл= f (  )
)
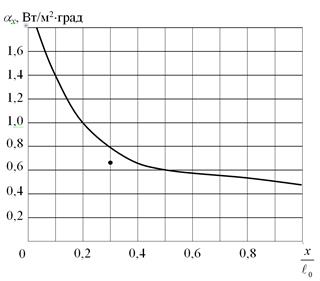
Рисунок 2.11 – График функции αх= f (  )
)
Задача 2.3
Найти поверхность теплообмена для гетерогенного реактора с графическим замедлителем. Мощность реактора Q =800 МВт. Температура стенок трубок
tW =950°С, диаметр 20мм. В качестве охладителя использован гелий. Температура гелия на входе в реактор t1 =150°С, на выходе t2 =750°С, давление 10 бар. Поток нейтронов предполагается равномерным. Активная зона реактора имеет форму куба со стороной 3,0 м. Живое сечение для прохода гелия составляет 1/3 от всего сечения активной зоны.
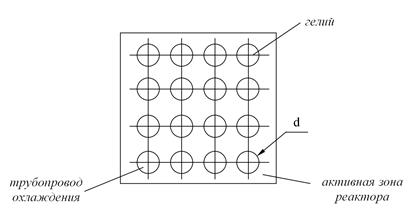
Рисунок 2.12
Теплоемкость гелия сp=5192 Дж×кг/град при t=0-100°С, Р=1-200 бар.
Решение
Расход гелия на охлаждение будет равен:
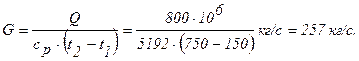
Площадь живого сечения для прохода гелия:
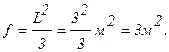
Скорость гелия в реакторе:
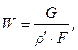
где ρ´ - плотность гелия, подсчитываемая при средней температуре охладителя и давлении 10 бар, т.е.:

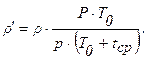
Здесь ρ – плотность гелия при нормальных условиях (р=1,02 бар, Т0=273 К), 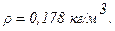
Тогда:
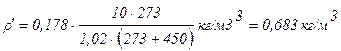 .
.
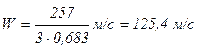 .
.
Для вычисления коэффициента теплоотдачи a определим режим движения в трубопроводе охлаждения по величине критерия Re. В качестве определяющей температуры принимаем среднюю температуру гелия tср = 450°С.
Параметры гелия при tср = 450°С, Р = 10 бар:
ср =5192 Дж/кг∙град, m = 3,6∙10-5 кг/м×с, l =0,215 Вт/м∙град.
Параметры гелия при 950°С:
ср =5192 Дж/кг∙град, m = 5,1∙10-5 кг/м×с, l =0,3 Вт/м∙град, Рr=0,882.
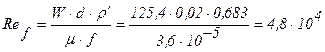 ;
;
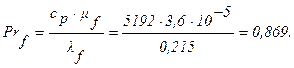
Значение критерия Ref >104. Принимаем течение в трубах турбулентным. Поэтому расчет коэффициента теплоотдачи будем проводить по формуле 2.21:
Тогда:
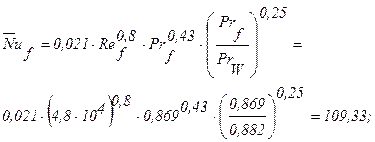
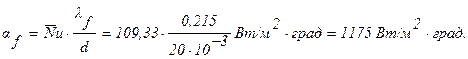
Поверхность теплообмена:
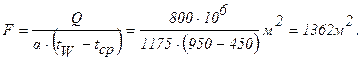
Количество труб для прохода гелия:
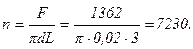
Задача 2.4
Сопло жидкостного ракетного двигателя (ЖРД) охлаждается одним из компонентов топлива – азотной кислотой, которая подается вдоль кольцевого канала. Суммарный (лучистый и конвективный удельный тепловой поток, поступающий в стенку сопла на участке между сечениями 1-1 и 2-2, равен 6 МВт/м2. Массовый расход охлаждающей жидкости равен 10 кг/с. Площадь поверхности участка сопла, через которую происходит теплообмен, - 0,01 м2. Средняя температура жидкости в сечении 1-1 равна 40°С. Внутренний и внешний диаметры охлаждающего тракта на участке 1-2 равны, соответственно, 120 мм и 124 мм. Определить подогрев охлаждающей жидкости и температуру стенки сопла со стороны жидкости на участке
1-2. Физические параметры азотной кислоты при 40°С: сf=1890 Дж/кг∙град, mf=0,75∙10-3 Н×с/м2, lf=0,328 Вт/м∙град, rf =1430 кг/м3.
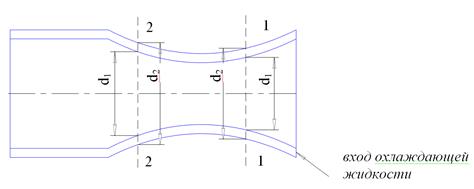
Рисунок 2.13
Решение.
Тепловой поток, образующийся при сгорании компонентов топлива в камере сгорания ЖРД, через стенки камеры идет на нагрев охлаждающей жидкости на участке сопла 1-2 от температуры t1 до температуры t2. Тогда:
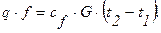
Здесь:
q – удельный тепловой поток, Вт/м2; f – поверхность теплообмена, м2;
сf – удельная теплоемкость охлаждающей жидкости (азотной кислоты), Дж/кг×град; G – массовый расход, кг/с.
На участке 1-2 жидкость нагревается до температуры:
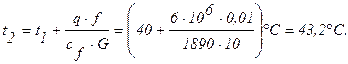
Перегрев охлаждающей жидкости, таким образом, составляет 3,2°С.
Средняя температура жидкости на участке 1-2:
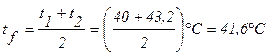 .
.
Температура стенки сопла со стороны жидкости равна:
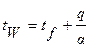 ,
,
где tf - средняя температура жидкости; a - коэффициент теплоотдачи от внутренней стенки к жидкости.
Для определения режима течения в кольцевом канале определяем значение критерия Рейнольдса.
Плоскость поперечного сечения канала
 .
.
Здесь d1, d2– внутренний и внешний диаметры канала.
Скорость охлаждения жидкости
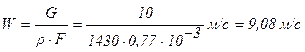 .
.
Критерий Рейнольдса равен:
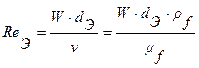 .
.
Здесь dЭ – эквивалентный диаметр поперечного сечения (кольцевого канала).
Для кольцевого канала dЭ= d2 - d1.
Откуда:
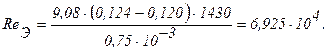
Критерий ReЭ>1×104. Принимаем течение в кольцевом канале турбулентным /27/.
Средний коэффициент теплоотдачи на внутренней стенке при турбулентном течении газов и капельных жидкостей в кольцевых каналах можно рассчитать по уравнению (2-21):
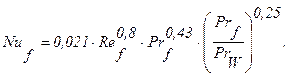
Принимаем в первом приближении tW=40°C. Тогда из условий задачи будем иметь:
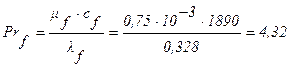 ;
;
PrW = Prf .
Откуда:
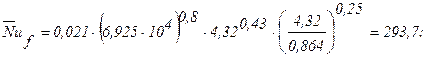

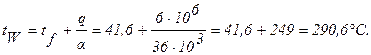
Более точное значение температуры стенки может быть получено путем последовательного уточнения физических параметров охлаждающей жидкости.
Задача 2.5
Определить коэффициент теплоотдачи в первой ступени теплообменного аппарата атомного реактора. Средняя скорость теплоносителя (Na-25%, K-75%) W=5м/с, средняя температура t=400°С. Диаметр трубы, по которой течет теплоноситель, равен d=30мм. Тепловой поток по длине трубы принять постоянным.

Рисунок 2.14
Решение
Определяем режим течения в трубе при средней температуре теплоносителя
tf =400°С. Параметры теплоносителя : lf =20 Вт/м×град; nf = 30,8×10-8 м2/с;
af = 0,35×10-4 м2/с (см. табл. 17 /20/).
Тогда:
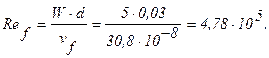
Принимаем режим течения теплоносителя турбулентным.
Для жидких металлов для определения коэффициента теплообмена в цилиндрических трубах при турбулентном течении используется выражение (формула (2.33)):

где: 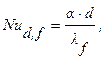
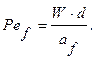
Определяем значение критерия Pef :
 .
.
Откуда:
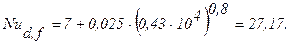
Коэффициент теплоотдачи
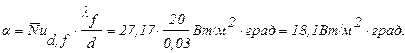
Задача 2.6
Железный электропровод диаметром d = 10 мм охлаждается поперечным потоком воздуха, скорость и средняя температура которого, соответственно, равны
W = 2м/с, tf= 15°С. Определить коэффициент теплоотдачи от поверхности электропровода к воздуху и допустимую силу тока в электропроводе при условии, что температура электропровода не должна превышать tW = 95°С. Удельное электросопротивление электропровода r = 0,98 Ом×мм2/м. Параметры воздуха при tf = 15°С: коэффициент теплопроводности lf = 2,552×10-2 Вт/м×град, коэффициент кинематической вязкости nf = 14,64×10-6 м2/с.

Рисунок 2.15
Решение
Критерий Рейнольдса при поперечном обтекании одиночного цилиндра (трубы):
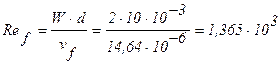 .
.
При обтекании одиночной трубы воздухом применяются следующие упрощенные зависимости для расчета среднего значения коэффициента теплоотдачи (формулы 2.26 и 2.27):
при Ref = 5¸1×103 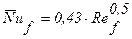 ;
;
при Ref = 1×103¸2×105 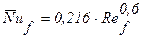 .
.
Тогда:
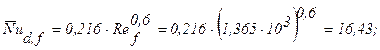
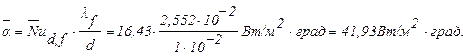
Допустимый ток в электропроводе определяется из уравнения:
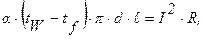
где R – электрическое сопротивление электропровода длиной ℓ, т.е.:
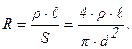
Здесь S –поперечное сечение электропровода.
Тогда:
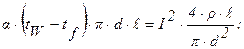

Задача 2.7
Определить коэффициент теплоотдачи и тепловой поток на единицу длины в поперечном потоке воздуха для трубы d =36 мм, если температура ее поверхности tW = 80°С, температура воздуха tf = 20°С и скорость W = 5 м/с. Параметры воздуха при tf = 20°С: коэффициент теплопроводности lf = 2,593×10-2 Вт/м×град, коэффициент кинематической вязкости nf = 15,06×10-6м2/с.
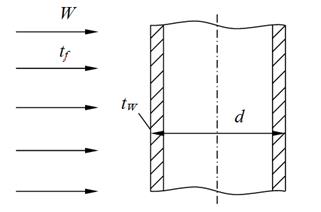
Рисунок 2.16
Решение
Критерий Рейнольдса при обтекании равен:
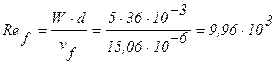 ;
;
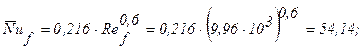
Коэффициент теплоотдачи:
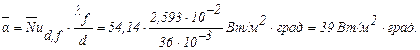
Тепловой поток на единицу длины:
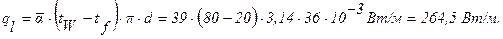
Задача 2.8
Для теплообменного устройства определить коэффициент теплоотдачи от горячего воздуха, протекающего по коробу квадратного сечения (ℓ =500 мм), к стенкам труб, по которым протекает вода. Средняя по длине температура воздуха в устройстве tf = 600°С, длина устройства 4 м, средняя скорость воздуха W= 18 м/с, расстояние между центрами труб S1 = S2 = 150 мм, диаметр трубы d = 75 мм, количество труб – 9.
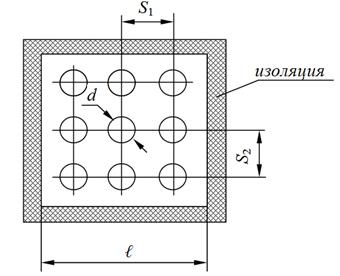
Рисунок 2.17
Решение
Определяем режим течения воздуха в коробе по значению критерия Рейнольдса ReЭ:
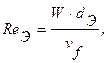
где dЭ – эквивалентный диаметр короба, равный 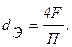
Здесь F – сечение канала короба, по которому протекает воздух, П – полный периметр сечения F;
nf – коэффициент кинематической вязкости.
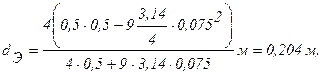
При t = 600°С nf = 96,89×10-6м2/с.
Тогда:
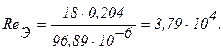
Принимаем режим движения в коробе турбулентным, поэтому для определения коэффициента теплоотдачи a от воздуха к стенкам труб можно использовать следующую формулу для продольного омывания пучков труб:
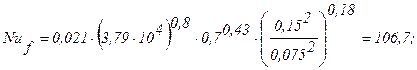
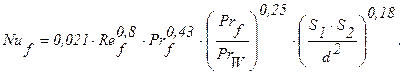
Из условий задачи (рабочая среда – воздух) можно принять, что 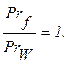
Тогда:
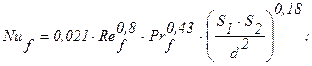
Prf = 0,70;
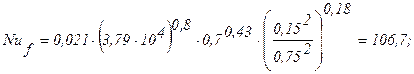
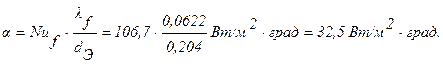
Задача 2.9
Определить потерю тепла путем конвекции вертикальным изолированным паропроводом диаметром d = 100 мм и высотой ℓ = 4 м, если температура наружной стенки tW = 180°С, а температура среды (воздуха) tf = 30°С.
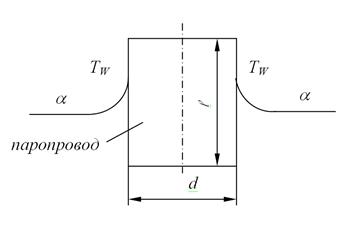
Рисунок 2.18
Решение
Определяем режим течения воздуха у паропровода.
При tf = 30°С параметры воздуха равны: rf = 1,165 кг/м3; ;nf = 16×10-6 м2/с;
Сpf = 1,005 кДж/кг×град; lf = 2,67×10-2Вт/м×град; af = 22,9×10-6 м2/с; Prf = 0,701;
mf = 18,6×10-6 Н×с/м2.
При tW = 180°С параметры воздуха равны: rf = 0,779 кг/м3; ; Prf = 0,681;
Сpf = 1,022 кДж/кг×град; lf = 3,78×10-2Вт/м×град; af = 47,5×10-6 м2/с; nf = 32,49 м2/с;
mf = 25,3×10-6 Н×с/м2.
Коэффициент объемного расширения:
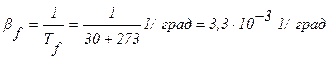 .
.
Критерий Gr f ,ℓ равен:
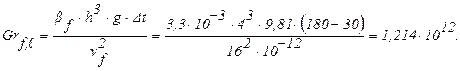
Тогда 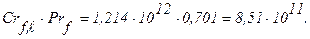
В условиях свободной конвекции при 103 <Crf × Pf < 109 – ламинарный режим течения для вертикальных поверхностей (трубы, пластины) и при Crf × Pf >109 – турбулентный режим.
Используя формулу (2.32) получим:
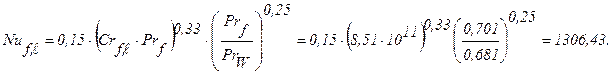
Откуда
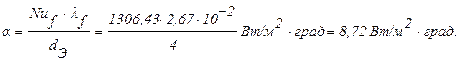
Искомая потеря тепла
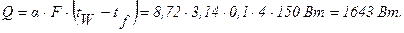
Убеждаемся, что для воздуха в пределах температур 30¸180°С
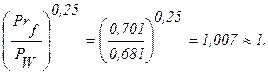
Задача 2.10
Сверхзвуковой самолет летит на высоте Н=15 км со скоростью Мн=1,8 (где число Мн – число Маха, равное 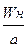 (Wн – скорость набегающего потока, а – скорость звука); крыло самолета имеет тонкий симметричный профиль с хордой b = 1,2 м. Определить удельные тепловые потоки аэродинамического нагрева в отдельных точках профиля крыла, расположенных от передней кромки на расстоянии
(Wн – скорость набегающего потока, а – скорость звука); крыло самолета имеет тонкий симметричный профиль с хордой b = 1,2 м. Определить удельные тепловые потоки аэродинамического нагрева в отдельных точках профиля крыла, расположенных от передней кромки на расстоянии 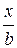 =0,05; 0,1; 0,5; 0,9, если в данный момент температуры в этих точках tW =+23; +3; -17; -37°С и полет совершается с нулевым углом атаки.
=0,05; 0,1; 0,5; 0,9, если в данный момент температуры в этих точках tW =+23; +3; -17; -37°С и полет совершается с нулевым углом атаки.
Указание: при решении задачи такое симметричное крыло можно рассматривать как тонкую пластину, пренебречь влиянием возможных скачков уплотнения у передней кромки и принять параметры воздуха на внешней границе пограничного слоя как в невозмущенном потоке.
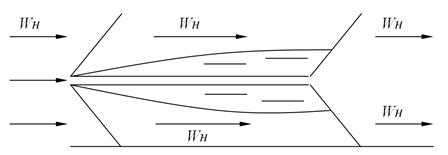
Рисунок 2.19
Решение
1.Определяется температура восстановления по выражению (2.35):
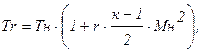
где r = 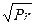 – для ламинарного пограничного слоя;
– для ламинарного пограничного слоя;
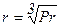 для турбулентного пограничного слоя.
для турбулентного пограничного слоя.
Для воздуха Pr=0,7; к = 1,4; Тн =216,5К (Н=15 км), отсюда Tr = 335 и 342 К соответственно для ламинарного и турбулентного пограничных слоев.
2. Определяющая температура Тэф вычисляется по выражению (/14/, стр.241):
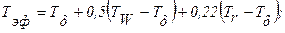
в данном случае Тd = Тн =216,5 К (согласно указанию).
Результаты расчета и соответствующие этим температурам теплофизические свойства воздуха сведены в таблицу.
| tW, °C | Tэф, К | tэф, °С | m, 10-6 ×Н×с/м2 | l, 10-2× ×В/м×град | Ср кДж/кг× ×град | Р |
| +23 | +10 | 17,66 | 2,51 | 1,005 | 0,705 | |
| +3 | 17,17 | 2,44 | 1,005 | 0,707 | ||
| -17 | -10 | 16,68 | 2,36 | 1,009 | 0,712 | |
| -37 | -20 | 16,19 | 2,28 | 1,009 | 0,716 |
3. Скорость набегающего потока воздуха:
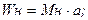
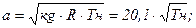 а = 295 м/с;
а = 295 м/с;
Wн = 1,8×296 м/с = 533 м/с.
4. Расчет теплоотдачи в точке 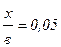 с температурой
с температурой
tW = +23°С:
при rн = 0,196 кг/м3 (Н=15км) и х = 0,05в =0,05×1,2= 0,06 м имеем:
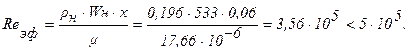
При ламинарном пограничном слое значение коэффициента теплоотдачи вычисляется по формуле (2.38):
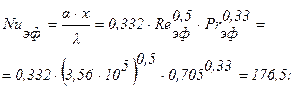
a = 74,1 Вт/м×град;
q = a×(Tr -TW) = 74,1×(335-296) Вт/м2 = 2,88×103 Вт/м2.
5. При турбулентном пограничном слое местное значение коэффициента теплоотдачи вычисляется по формуле (2.37):
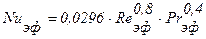
Результаты расчета получаются следующими:
Nuэф = 1243;
a = 253,5 Вт/м2×град
q = 16,7×103 Вт/м2.
6. Расчет теплоотдачи в остальных двух точках можно вести по данным, полученным для предыдущей точки, так как в этих точках пограничный слой тоже турбулентный и отличается только своим расположением и температурой tW (или tэф):
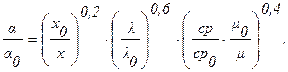
Для точки 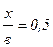 с tW = -17°C:
с tW = -17°C:
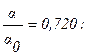 a = 253,5 × 0,720 Вт/м2×град = 182,6 Вт/м2×град, q =15,7 ×103Вт/м2.
a = 253,5 × 0,720 Вт/м2×град = 182,6 Вт/м2×град, q =15,7 ×103Вт/м2.
Для точки 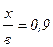 с tW = -37°:
с tW = -37°:
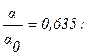 a = 253,5 × 0,635 = 161,1 Вт/м2×град; q =17,1 ×103 Вт/м2.
a = 253,5 × 0,635 = 161,1 Вт/м2×град; q =17,1 ×103 Вт/м2.
Задача 2.11
Определить удельный тепловой поток аэродинамического нагрева в тех же точках профиля крыла, которые рассматриваются в задаче 2.10, если самолет летит на той же высоте со скоростью Мн =1,5 и с углом атаки крыла y = 10° (рисунок 2.20).
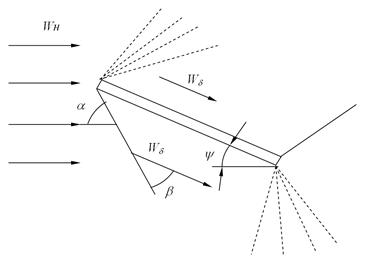
Рисунок 2.20
Указание: Профиль крыла рассматривается как тонкая пластина, параметры воздуха на внешней границе пограничного слоя рассчитываются снизу как за косым скачком уплотнения, а сверху как параметры воздуха после обтекания тупого угла потоком со сверхзвуковой скоростью.
Решение
На высоте Н = 15 км Тн= 216,5 К и rн = 0,196 кг/м3 (см /13/, приложение VI, /19/, приложение)
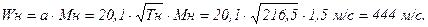
Параметры потока воздуха за косым скачком уплотнения, обтекающего крыло снизу (с индексом d)определяется следующим образом:
1 Пользуясь графиком из /13/, приложение ХХI, находят угол наклонения фронта косого скачка a к направлению набегающего потока; если угол отклонения потока w =10° (равен углу атаки крыла y) и Мн = 1,5, то a = 58°, sina = 0,847,
sin2a = 0,715;
2.  ;
;
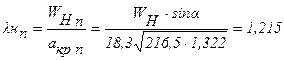 .
.
3. 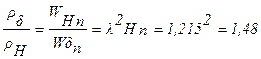 ;
;
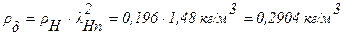 .
.
4. 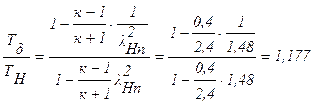 ;
;
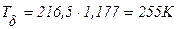 .
.
5. 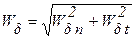 ,
,
где 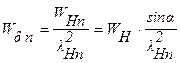 ;
;
 ;
;
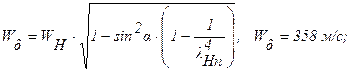
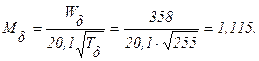
Параметры потока со сверхзвуковой скоростью воздуха над крылом после обтекания тупого угла (с индексом d) определяются следующим образом:
1. 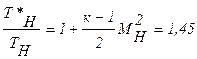 ;
;
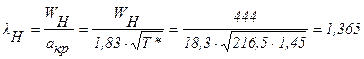 ;
;
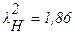 .
.
2. Пользуясь графиком приложения XXI, /13/, находим значение приведенной скорости после обтекания тупого угла 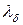 ; если
; если 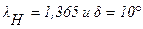 , то
, то 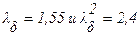 ;
;
3. 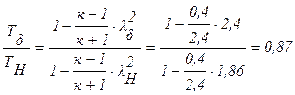 ;
;
4. 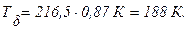
5. 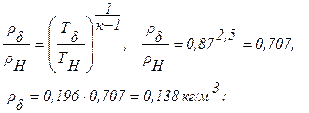
6. 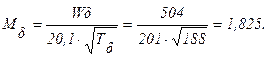
Для определения коэффициентов теплоотдачи и удельного теплового потока как снизу, так и сверху крыла используется метод, изложенный в задаче 2.10
Результаты расчета сведены в таблицу.
| х/в | tW , °С | Tr | a | q | Tr | a | q |
| К | Вт/м2×град | Вт/м2 | К | Вт/м2×град | Вт/м2 | ||
| снизу крыла | сверху крыла | ||||||
| 0,05 | +23 | 71,4 | 117,2 | 58,6 | |||
| 0,10 | +3 | 9,01×103 | 182,0 | 437×103 | |||
| 0,05 | -17 | 180,8 | 10,14×103 | 131,8 | 580×103 | ||
| 0,09 | -37 | 161,1 | 12,21×103 | 117,1 | 750×103 |
Задача 2.12
В теплообменном аппарате жидкость с водяным эквивалентом
С1= 116 Вт/град охлаждается от t1¢= 120°C до t1²= 50°С водой при температуре t2¢=10°С для которой С2=584 Вт/град. Определить потребную поверхность нагрева при схеме прямотока и противотока, если коэффициент теплопередачи к=2336 Вт/м2×град.

Рисунок 2.21 Схемы движения теплоносителей в теплообменниках
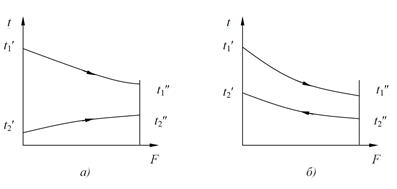
Рисунок 2.22 Характер изменения температуры теплоносителей при
прямотоке (а) и противотоке (б) при  , F - поверхность теплообмена.
, F - поверхность теплообмена.
Решение
Конечная температура воды определяется соотношением (формула(2.42)):
 .
.
Откуда:
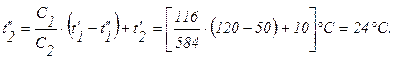
а) при прямотоке:
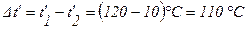 ;
;
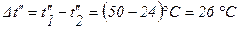 ;
;
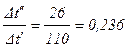 .
.
Среднелогарифмический напор (формула (2.46)):
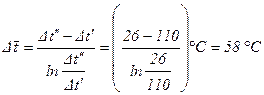 .
.
Потребная поверхность нагрева при прямотоки равна:
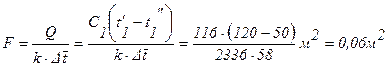
б) при противотоке:
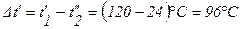 ;
;
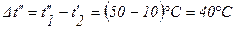 .
.
Среднелогарифмический напор :
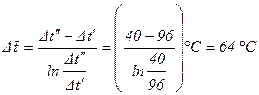 .
.
Потребная поверхность нагрева при прямотоки равна:
 .
.
Дата добавления: 2015-12-26; просмотров: 21924;
