Основные термодинамические сведения

3.1.1 Излучение абсолютно черного тела

Переход теплоты в энергию излучения в телах связан с внутриатомными процессами, обусловленными температурными влияниями. Энергия излучения тела может поглощаться другими телами и вновь трансформироваться в теплоту.

Передача теплоты излучением происходит в видимой (длина волны излучения l = 0,4¸0,76 мкм) и в инфракрасной (l = 0,76¸1000 мкм) областях спектра. При температурах в реальных теплотехнических процессах основная доля энергии излучается в ближайшей инфракрасной области (l =0,76-25 мкм). Излучение в видимой области спектра имеет существенное значение только при очень высоких температурах.

Различают монохроматическое, или спектральное, и интегральное излучения.

Спектральным (монохроматическим) излучением называется излучение в узком интервале длин волн от l до l + dl. Все описывающие его величины относятся к интервалу длин волн dl (или частот dn) и обозначаются индексом l (или n).

Интегральным называется суммарное излучение во всем интервале длин волн от l = 0 до l = ¥.

Абсолютно черным телом называется тело, которое полностью поглощает все падающее на него излучение, независимо от направления его распространения, спектрального состава и состояния поляризации.

Излучение, испускаемое в любом направлении, характеризуется интенсивностью излучения.

Спектральная интенсивность изучения (рисунок 3.1) определяется как энергия излучения, испускаемая в единицу времени, в единице узкого интервала волн dl, включающего длину волны l, единицей площади проекции элемента поверхности dАр, перпендикулярной направлению (b, Θ), в единице элементарного телесного угла dw, осью которого является выбранное направление (b, Θ).

Здесь b, Θ соответственно, полярный и азимутальный углы. Угловое положение Θ=0 произвольное.

Рисунок 3.1 - Спектральная интенсивность излучения абсолютно черной поверхности

Спектральная и интегральная интенсивности излучения абсолютно черного тела связаны между собой интегральным соотношением:

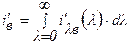. (3.1)

Здесь индексы: ′ – величина, имеющая направление; в – абсолютно черное тело.

Энергия излучения, испускаемая единицей площади элшемента абсолютно черной поверхности dA в единицу времени, в единице бесконечно малого интервала длин волн dl, включающего длину волны l,в единицу элементарного телесного угла dω, осью которого является направление (b, Θ), называется направленной спектральной силой излучения абсолютно черной поверхности е'_l(l, β, Θ).

Для абсолютно черной поверхности

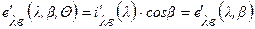. (3.2)

Уравнение (3.2) известно как закон Ламберта. Поверхности, излучающие по закону Ламберта, называются идеально диффузными поверхностями.

Энергия излучения, испускаемая единицей площади поверхности dA в единицу времени, в единице интервала длин волн dl, включающего длину волны l, называется полусферической спектральной поверхностной плотностью потока излучения поверхности е'_l(l).

Для абсолютно черного тела

. (3.3)

Энергия излучения в телесном угле, ограниченном пределами β₁ и β₂, а также Θ₁ и Θ₂, равна:

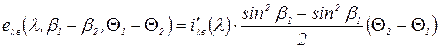. (3.4)

Закон спектрального распределения поверхностной плотности потока излучения Планка (излучение в вакууме) определяется выражением:

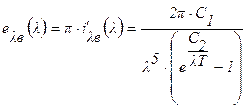, (3.5)

где С₁ и С₂ – постоянные: С₁= h×с₀² = 0,59544×10^-16 Вт×м², h – постоянная Планка, h = 6,626×10^-34 Дж×с, с₀ – скорость распространения электромагнитного излучения в вакууме, с₀ =2,9979×10⁸ м/с; , к – постоянная Больцмана, к = 1,38×10^-23Дж/К; Т – температура тела.

Длина волны l_max, которой соответствует максимум поверхностной плотности потока излучаемой энергии е_lв(l), определяется законом смещения Вина:

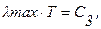(3.6)

где С₃ –постоянная, С₃ = 2,8978×10^-3 м×К

Полусферическая интегральная поверхностная плотность потока излучения равна:

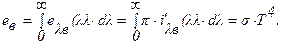(3.7)

Это соотношение известно как закон Стефана-Больцмана,
σ = 5,6693×10^-8 Вт/м²×К⁴ (расчетное значение)

Доля полусферической интегральной поверхностной плотности потока излучения, испускаемого в полосе спектра l₁ - l₂, определяется соотношением:

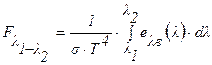(3.8а),

или

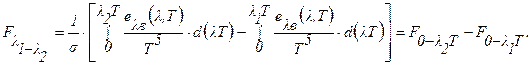(3.8б).

Имеются составленные таблицы значений 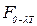/13/. В /13/ для расчетов 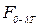рекомендуется использовать следующие полиномы:

(3.9);

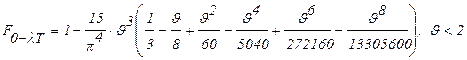(3.10),

где , С₂ – постоянная в уравнении Планка.

3.1.2 Определение радиационных свойств нечерных поверхностей

Степенью черноты e называется отношение энергии, излучаемой телом при температуре Т, к энергии излучения абсолютно черного тела при той же температуре. Излучательная способность тела зависит от температуры тела, длины волны, которой соответствует испускаемое излучение, и угла, под которым испускается излучение.

Попадая на какие либо тела, тепловое излучение может отражаться, поглощаться или пропускаться этими телами. Падающее излучение имеет свойства, присущие излучению источника. Отношения энергий поглощенного, отраженного и пропущенного телом излучения к энергии падающего на тело излучения называются, соответственно, поглощательной (a), отражательной (r) и пропускательной (d) способностями.

Для спектрального и интегрального излучений различают направленные и полусферические степени черноты и поглощательные способности, двунаправленные, полусферические, направленно-полусферические и полусферически-направленные отражательные способности.

Закон Кирхгофа устанавливает связь между способностями тела излучать и поглощать энергию:

(3.11)

Указанное равенство справедливо без ограничений для случая термодинамического равновесия в изотермической замкнутой полости /13/.

Нечерными называются тела, коэффициенты поглощения которых менее 1. Все нечерные тела могут быть разделены по характеру спектра излучения на серые тела и тела с селективным излучением. Серым называется тело, которое поглощает одну и ту же долю падающего на него излучения во всем интервале длин волн. Серые тела обладают сплошным спектром излучения, подобным спектру излучения абсолютно черного тела, а их поглощательная способность во всем интервале длин волн в одинаковое число раз меньше, чем у абсолютно черного тела.

В отличие от серых тел, тела с селективным излучением могут излучать и поглощать энергию лишь в определенных, характерных для каждого тела областях спектра.

3.1.3 Определение радиационных свойств с помощью классической электромагнитной тории

Классическая электромагнитная тория с использованием решений уравнений Максвела устанавливает связь между радиационными, электрическими и магнитными свойствами вещества. Для спектральной степени черноты металлов в направлении нормали предложена формула, известная как формула Хагена – Рубенса:

(3.12),

где п – показатель преломления металла; l₀ – длина волны излучения в вакууме, мкм; r_e – удельное электрическое сопротивление, Ом×см.

3.1.4 Равновесная температура

Общим критерием, определяющим свойства данной селективной поверхности, является отношение направленной интегральной поглощательной способности поверхности a ¢(b, q, Т), подвергаемой воздействию падающего солнечного излучения, к полусферической интегральной степени черноты этой поверхности e (Т). Отношение a ¢/e для падающего солнечного излучения является критерием, определяющим теоретическую максимальную температуру, которая может быть достигнута некоторой изолированной от других воздействий поверхностью при падении на нее солнечного излучения:

(3.13)

где Т_равн – достигнутая равновесная температура; q_i = 1394 Вт/м² – поверхностная плотность потока солнечного излучения; b - угол падения солнечного излучения.
3.1.5 Теплообмен излучением между изотермическими поверхностями

Доля энергии излучения, испускаемого одной поверхностью и достигающего другой поверхности, определяется как угловой коэффициент между двумя поверхностями и зависит от геометрической ориентации поверхностей относительно друг друга.

Рисунок 3.2 - Теплообмен излучением между двумя элементарными
площадками

Угловые коэффициенты для расчета теплообмена между двумя элементарными площадками dA₁ и dA₂, между элементарной площадкой dA₁ и поверхностью конечных размеров А₂, между двумя поверхностями конечных размеров А₁ и А₂ определяются, соответственно, соотношениями:

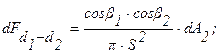(3.14)

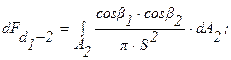(3.15)

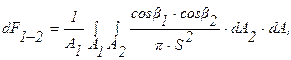(3.16)

где b₁ и b₂ – углы между нормалями к площадкам и линией S, соединяющей их.

Угловые коэффициенты dF_{d2- d1}, F_{2- d1}, F_2-1 определяются в соответствии с соотношениями взаимности:

(3.17)

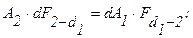(3.18)

(3.19)

Уравнение для определения потока результирующего излучения записываются в виде:

(3.20)

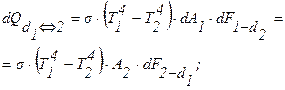(3.21)

(3.22)

3.1.6 Теплообмен излучением между поверхностями конечных размеров

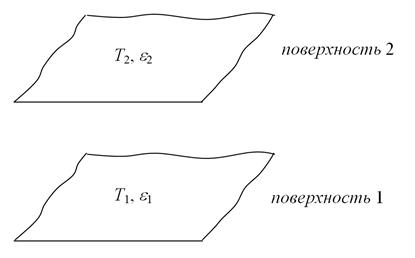
Рисунок 3.3

Плотность теплового потока между двумя серыми пластинами (рисунок 3.3) будет равна:

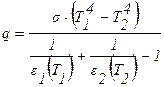, (3.23)

где e₁, e₂, Т₁, Т₂, соответственно, степени черноты и температуры пластин 1 и 2.