Примеры решения задач. Абсолютно черное тело при Т = 1110К излучает в космосе.
Задача 3.1
Абсолютно черное тело при Т = 1110К излучает в космосе.
а) Каково отношение спектральных интенсивностей излучения абсолютно черного тела при l1= 1 мкм и l2 = 5 мкм?
Решение
Из закона спектрального распределения поверхностной плотности потока излучения Планка (формула 3.5) будем иметь:
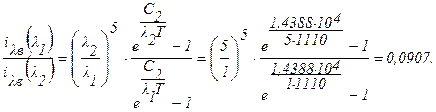
Здесь принято С2 = 1,4388 × 10-2 м × К = 1,4388 × 104 мкм × К.
б) Какая доля полусферической поверхностной плотности потока излучения приходится на область от 1 до 5 мкм?
Решение
Обозначим: l1 = 1 мкм, l2 = 5 мкм.
Доля полусферической интегральной поверхностной плотности потока излучения, испускаемого в полосе спектра l1-l2, определяется формулой:

Решения, которые могут быть получены путем непосредственного интегрирования интегралов F0 -lT, не рассматриваем.
Решение с использованием таблиц, содержащих значения F0 -lT (см., например, таблица А-5, приложения А/13/):
l1Т = 1 × 1110 мкм ×К = 1110 мкм ×К = 0,111×10-2 м ×К;
l2Т = 5 × 1110 мкм ×К = 5550 мкм ×К = 0,555×10-2 м ×К;
F0 -l2T = F0 – 0,555 × 10-2 =0,69655;
F0 -l1T = F0 – 0,111 × 10-2 = 0,00101;
Fl2 -l1 = F0 -l2T - F0 -l1T = 0,69655 - 0,00101=0,69554 » 0,696.
3. Решение с помощью полиномов(/13/, приложение А):



Так как J1 и J2 более 2, то для вычисления функций F0 -lT применим следующий полином (формула 3.9):

Откуда, при m = 1 будем иметь:

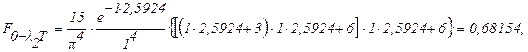
Fl2 -l1 = F0 -l2T - F0 -l1T = 0,68154 - 0,0010 » 0,68054.
С точностью до 2% решения, полученные с помощью таблиц (Fl2 -l1 = 0,69554) и полиномов (даже при m = 1) совпадают.
в) Какой длине волны соответствует максимум в спектре излучения этого абсолютно черного тела?
Из закона смещения Вина (формула 3.6) будем иметь
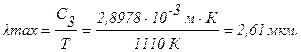
г) Какова плотность потока излучения (кВт/м2), испускаемого этим телом в диапазоне 1 £ l £ 5 мкм?
Используем закон Стефана-Больцмана (формула (2.23) /13/):
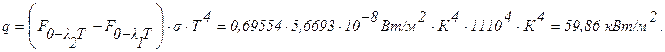
Задача 3.2
Источником абсолютно черного излучения является отверстие в печи с температурой 1390 К. Какая часть излучения задержится кольцевым диском? Какая часть пройдет через отверстие в диске?

Рисунок 3.6
Решение
а) Какая часть излучения задержится кольцевым диском?
Полусферическая интегральная поверхностная плотность потока излучения равна (формула (3.3):

Интегральная поверхностная плотность потока излучения в телесном угле, ограниченном пределами b1 и b2 и Q1 и Q2, равна (формула (3.4):
 .
.
Кольцевым диском задержится следующая часть потока излучения:

Углы b1 и b2 определяются из рассмотрения прямоугольных треугольников, содержащих эти углы:
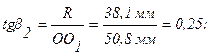
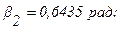
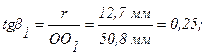



б) Какая часть излучения пройдет через отверстие в диске?

В этом случае:
b1 = 0;
b2 = 0,2449 рад;

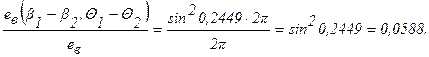
Задача 3.3
Направленная степень черноты серой поверхности изображена на графике. Свойства изотропны относительно азимутального угла Q.

Рисунок 3.7
а) Чему равна полусферическая степень черноты этой поверхности?
Решение
Полусферическая интегральная степень черноты определяется выражением (3.6б /13/):

где e¢(b,Q, ТА) – направленная интегральная степень черноты; ТА – температура поверхности; dw – телесный угол излучения, 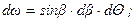 Ç – интегрирование по полусфере.
Ç – интегрирование по полусфере.
По условию задачи, степень черноты серой поверхности не зависит от температуры поверхности ТА, т.е.:
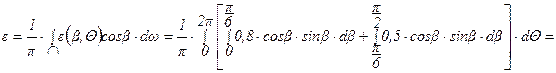
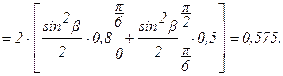
б) Если поток падающего черного излучения при температуре 93°С равномерно распределяется по всем направлениям, то какая доля падающей энергии будет поглощаться этой поверхностью?
Решение
В нашем случае (черный излучатель) интенсивность падающего излучения не зависит от угла падения, следовательно:
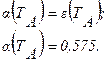
в) Если эту поверхность поместить в окружающую среду с температурой 0 К, то каким должен быть поток энергии, подводимой к 1 м 2 этой поверхности, чтобы ее температура оставалась равной 556 К?
Решение
Поток энергии, подводимой к поверхности, должен быть равным потоку излучения:
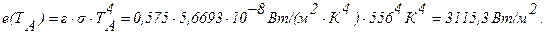
Задача 3.4
Спектральная поглощательная способность al(l) селективной поверхности SiO – Al может быть приближенно представлена графиком, приведенном ниже (рисунок 3.8). Поверхность находится на земной орбите вокруг Солнца, и на нее в направлении нормали падает поток солнечного излучения qi=1393 Вт/м2. Какова равновесная температура поверхности при условии, что al не зависит от угла и температуры поверхности.

Рисунок 3.8
Решение
Так как перенос тепла осуществляется только изучением, то энергии поглощаемого и испускаемого излучения будут равны:

где Qа – энергия поглощения поверхности площадью А; a¢n – направленная по нормали интегральная поглощающая способность; a0-1,5 , a1,5-¥ - полусферическая поглощательная способность в диапазоне длин волн Dl = (0 – 1,5) мкм и Dl = (1,5 – ¥) мкм соответственно; F0 – 1,5(TR), F1,5 – ¥ (TR) – доля интегрального потока падающего солнечного излучения в диапазоне длин волн, соответственно,
Dl = (0 – 1,5) мкм и Dl = (1,5 – ¥) мкм; TR – температура источника (Солнца),
TR = 5556 К.

где Qе – энергия излучения поверхности площадью А; e – полусферическая интегральная степень черноты; e0-1,5 , e1,5-¥ - полусферическая степень черноты в диапазоне волн Dl = (0 – 1,5) мкм и Dl = (1,5 – ¥) мкм соответственно;F0 – 1,5(TR), F1,5 – ¥ (TR) – доля интегрального потока излучения поверхности в диапазоне длин волн, соответственно, Dl = (0 – 1,5) мкм и Dl = (1,5 – ¥) мкм; Tе – равновесная температура поверхности.
Ввиду независимости интенсивности падающего излучения (источник: абсолютно черное тело (Солнце) с температурой Т = 5556 К) от направления, будем иметь равенство полусферических степени черноты и поглощательной способности, т.е.:

Полусферические интегральные в диапазоне волн Dl = (0 – 1,5) мкм и
Dl = (1,5 – ¥) мкм значения степени черноты и поглощательной способности будут равны:

Приравнивая Qa и Qе будем иметь:


Значения выражений F0 – 1,5(5556 К) и F1,5 – ¥ (5556 К) определяются по таблицам /13/
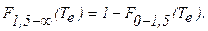
Значение Те определяется методом последовательных приближений:
Те = 665 К.
Задача 3.5
Диэлектрик с коэффициентом преломления n = 1,8 излучает в воздух. Какова направленная степень черноты в направлении, нормальном к поверхности, и в направлении, составляющем b =85° с нормалью?
Решение
Степень черноты при излучении диэлектрика в воздух в направлении нормали равна (см. формулу 4.51 /13/:
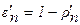 ;
;
 .
.
Из формулы Френеля (формула 4.48 /13/) будем иметь:

где c - угол преломления.
Для диэлектриков (формула 4.43, /13/):
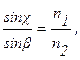
где п1 -коэффициент преломления воздуха, п1 = 1; п2 -коэффициент преломления диэлектрика, п2 = 1,8.
 c = 33,6°;
c = 33,6°;

Задача 3.6
Оцените спектральную отражательную способность алюминия в направлении нормали при температуре 293 К для длин волн l0 равных 5, 10, 20 мкм.
Решение
Из формулы Хагена-Рубенса для спектральной отражательной способности в направлении нормали будем иметь (формула 4.77 /13/). Размерности принимать: для l0 – в микрометрах, rе – в Ом×см.
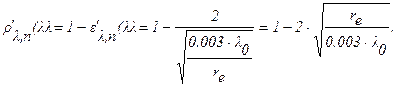
Из таблицы (4.3 /13/) для удельного электрического сопротивления алюминия можно принять rе = 2,82 × 10-6 Ом×см.
Тогда для r¢l,п(l) последовательно для l0 = 5, 10, 20 мкм будем иметь:
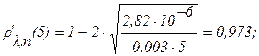

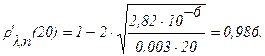
Задача 3.7
На полированное золото при температуре ТА = 30°С падает излучение от серого источника в направлении нормали при температуре ТR = 540°C. Найти поглощательную способность a¢п.
Решение
Направленная интегральная поглощательная способность равна (формула 3.14а /13/):
 .
.
здесь i – индекс для падающего излучения.
Для серого тела:

Тогда

Из закона Кирхгофа (формула 3.12 /13/) имеем:
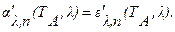
Поэтому

Из формулы Хагена-Рубенса (формула 4.77 /13/) следует, что изменение rе с температурой приводит к изменению  , пропорциональному
, пропорциональному 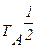 .
.
Тогда:
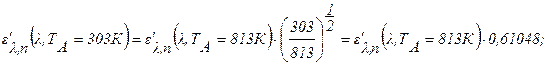

Имеем (формула 4.81б /13/):
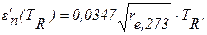
Размерность rе,273 в Ом×см, размерность ТR в К.
re равно (таблица 4.3 /13/):

Из формулы (4.80 /13/):
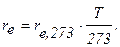
Тогда:

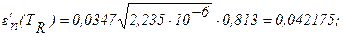

Задача 3.8
Свойства некоторой серой поверхности зависят от направления, как показано ниже (рисунок 3.9). Величина a¢ изотропна относительно угла Q.

Рисунок 3.9
а) Чему равно отношение a¢ (b = 0)/e (отношение направленной поглощательной способности к полусферической степени черноты) для этой поверхности?
Решение
По условию задачи имеем: a¢ (b =0) = 0,9; a¢ (b =0) =a¢п.
Из формулы (3.6б /13/):





б) Чему равна равновесная температура тонкой пластины, обладающей указанными выше свойствами, если она находится на земной орбите вокруг Солнца, и на нее действует поток солнечного излучения с поверхностной плотностью q=1394 Вт/м2? Принять, что пластина ориентирована перпендикулярно солнечным лучам и идеально изолирована со стороны, противоположной Солнцу.
Решение
Из формулы 3.13 при b = 0 имеем:
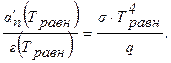

в) Чему равна равновесная температура, если пластина расположена под углом 60° к солнечным лучам?

Рисунок 3.10
Решение
Из формулы 3.13 при b = 60° имеем:
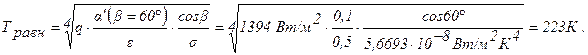
г) Чему равна равновесная температура, если пластина расположена перпендикулярно солнечным лучам, но не изолирована? Принять, что пластина очень тонкая и имеет с обеих сторон одинаковые направленные характеристики.
Количество поглощаемой энергии будет равно:

где А – площадь одной стороны пластины.
Количество излучаемой энергии:



Приравнивая энергии поглощаемого и испускаемого излучений, получим:


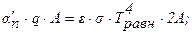

Задача 3.9
Вывести выражение для углового коэффициента  между элементарной площадкой, расположенной над центром диска, и диском радиуса R.
между элементарной площадкой, расположенной над центром диска, и диском радиуса R.

Рисунок 3.11
Решение
Угловой коэффициент  равен (формула3.15):
равен (формула3.15):
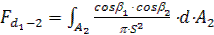
 .
.
Площадь dA2 выражается через локальный радиус диска r и угол Q:
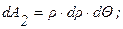
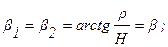

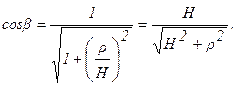
Q изменяется в пределах: 

r изменяется в пределах: 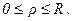

 .
.
Тогда:
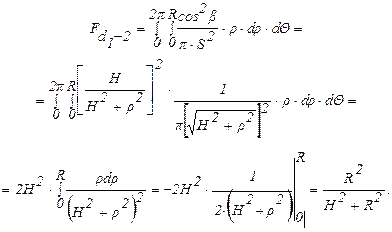
Задача 3.10
Каков поток результирующего излучения между двумя черными поверхностями dA1 и A2?
Условия задачи:
поверхности – поверхности задачи 3.9;
dA1=12,7´12,7 мм2;
Н=0,6096 м=609,6 мм;
Т1=1666 К;
Т2=555К;
R=152,4 мм.
Решение
Поток результирующего излучения (формула 3.21) равен:
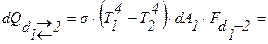


Задача 3.11
Две бесконечные параллельные серые пластины разделены тонким серым экраном.

Рисунок 3.12
а) Чему равна температура экрана ТS?
Решение
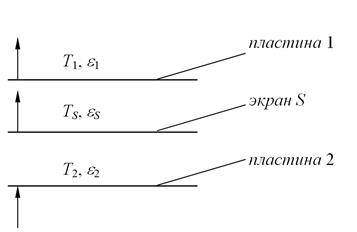
Рисунок 3.13
Теплообмен идет от поверхности 2 к поверхности 1; q2 – плотность потока, подводимого к поверхности 2, чтобы компенсировать поток результирующего излучения и тем самым поддержать заданную температуру поверхности. Тепло, подводимое к поверхности 2, отводится от поверхностей 3 и 1, т.е.
q2 = q3 = q1.
Тогда (формула 3.23):

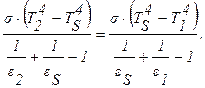
Обозначая и вычисляя:
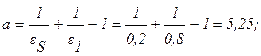
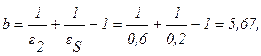
получим:

б) Какова плотность потока результирующего излучения от пластины 2 к пластине 1?
Решение

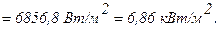
в) Каково отношение потоков излучения, передаваемых от пластины 2 к пластине 1, в присутствии экрана и без него?
Решение
Поток излучения, передаваемый от пластины 2 к пластине 1, в присутствии экрана, равен q2=6,86 кВт/м2. Результирующий поток излучения от пластины 2 к пластине 1 без экрана равен:
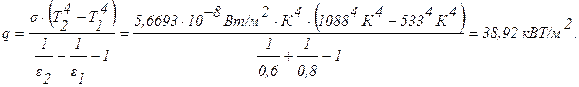
Отношение потоков, передаваемых от пластины 2 к пластине1, в присутствии экрана и без него:

Задача 3.12
Цилиндрический сосуд для хранения жидкого кислорода выполнен c двойными стенками, покрытыми слоем серебра, полусферическая интегральная степень черноты которого e1 = e2 =0,02. На наружной поверхности внутренней стенки температура равна t1 = -183°С, а температура на внутренней поверхности наружной стенки t2 =20°C. Расстояние между стенками мало, и поверхность А1 можно считать равной поверхности А2.
Вычислить тепловой поток, проникающий в сосуд через стенки путем лучистого теплообмена, если теплоотдающая поверхность А1 =А2 =А =0,157 м2.
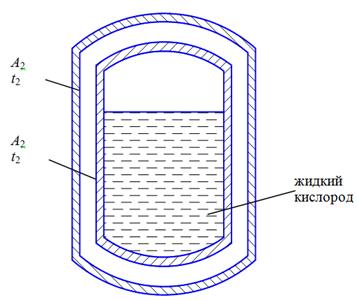
Рисунок 3.14
Решение
Ввиду примерного равенства поверхностей А1 и А2 для решения задачи можно применить формулу 3.23, используемую для расчета теплообмена излучением между двумя параллельными (зеркальными или диффузными) пластинами в виде:

Тогда:
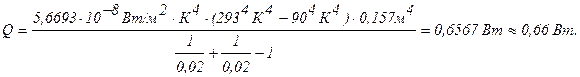
Задача 3.13
В канале, по которому движется горячий газ, температура газа измеряется при помощи термопары. Показание термопары t1=300°С, а температура стенки при установившемся тепловом режиме tW=200°С. Вычислить ошибку в измерении температуры газа, которая получается за счет лучистого теплообмена между горячим спаем термопары и стенкой канала, и истинную температуру газа. Степень черноты горячего спая термопары принять e1=0,8, а коэффициент теплоотдачи от газа к поверхности горячего спая a=58,2 Вт /м2×град.
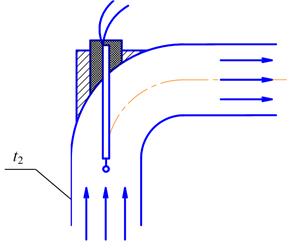
Рисунок 3.15
Решение
Составим уравнение теплового баланса для горячего спая термопары. Горячий спай термопары отдает тепло за счет излучения:

где Т1, ТW – соответственно, температуры горячего спая термопары и стенки канала; А1 – площадь горячего спая; Fd1-2 – угловой коэффициент между горячим спаем и стенкой канала.
Горячий спай получает тепло за счет конвенции:

где a - коэффициент теплоотдачи; t2 – температура горячего газа.
При установившемся режиме:
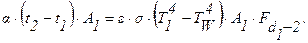
Ошибка в измерении температуры газа будет равна:
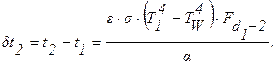
Практически все тепло с горячего спая падает на стенки канала, следовательно, Fd1-2=1. Тогда
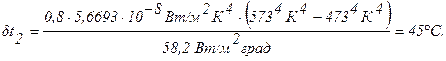
Истинная температура газа равна:

Задача 3.14
Показано, что в качестве первого приближения можно считать, что поглощательная способность СО2 при температуре Тg=833К и давлении 1,01 МН/м2 может быть представлена четырьмя полосами с вертикальными границами при длинах волн 1,8 и 2,2; 2,6 и 2,8; 4,0 и 4,6; 9 и 19 мкм соответственно. Какова интегральная степень черноты очень толстого слоя газа при той же температуре?
Направленная спектральная степень черноты объема однородного газа при длине пути излучения S (формула 13.42 /13/):
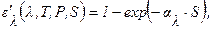
где al - коэффициент поглощения; Т, Р – температура и давление газа, соответственно.
При очень большой толщине слоя газа e¢l ®1 в полосах поглощения. Следовательно, газ будет излучать подобно черному телу в полосах поглощения. На непоглощающих участках между полосами el = 0.
Направленная интегральная степень черноты объема однородного газа при длине пути излучения S:

Следовательно, степень черноты есть доля излучения твердого тела, приходящаяся на интервалы полос поглощения, которая может быть определена с помощью коэффициентов F0-lTg /л. 13, таблица А5 приложения/.
Для данного случая они равны:
| l, мкм | lТg, мкм×К | F0-lTg | l, мкм | lТg, мкм×К | F0-lTg |
| 1,8 | 0,01285 | 4,0 | 0,34734 | ||
| 2,2 | 0,04338 | 4,6 | 0,44977 | ||
| 2,6 | 0,09478 | 9,0 | 0,83435 | ||
| 2,8 | 0,12665 | 0,97302 |
Тогда интегральная степень черноты будет равна:

Подставляя числовые значения, получим:
e¢=(0,04338-0,01285)+(0,12665-0,09478)+(0,44977-0,34734)+
+(0,97302-0,83435)=0,304.
Задача 3.15
Внутренние стенки печи прямоугольного сечения с размерами 0,305×0,305×1,22 м3 покрыты сажей и могут считаться черными. Печь заполнена продуктами сгорания при температуре 1950 К состава: 40 об.% СО2, 30 об.% водяного пара, остальное – азот.
Полное давление равно 0,202 МПа (2 атм). Используя график интегральной степени черноты СО2 и Н2О, рассчитать поток излучения, исходящий от газа на стенки.
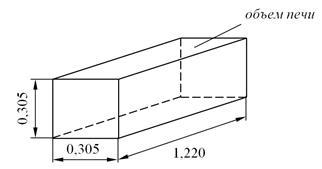
Рисунок 3.16
Решение
(Используется методология монографии /13, гл.17/.
Соотношение сторон объема печи: 0,305:0,305:1,22=1:1:4.
Средняя длина пути луча с учетом конечного значения оптической толщины Lе (/13/, таблица 17.1)
Lе= 0,81 × x,
где x – наименьшее ребро, х = 0,305 м.
Тогда:
Lе= 0,81 × 0,305 м = 0,247 м.
Учитывая, что двухатомный газ азот имеет низкое значение спектрального коэффициента поглощения, и потому он практически прозрачен для теплового излучения, для степени черноты смеси СО2, водяного пара и азота (непоглощающего газа) будем иметь:
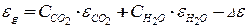 ,
,
где  - интегральные степени черноты углекислого газа и водяного пара в смеси непоглощающего газа при полном давлении 0,101 МПа (1 атм) (таблицы 17.11, 17.13 в /13/):
- интегральные степени черноты углекислого газа и водяного пара в смеси непоглощающего газа при полном давлении 0,101 МПа (1 атм) (таблицы 17.11, 17.13 в /13/):
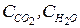 -поправки на давление к интегральной степени черноты, соответственно, СО2 и водяного пара (рисунки 17.12, 17.14 в /13/);
-поправки на давление к интегральной степени черноты, соответственно, СО2 и водяного пара (рисунки 17.12, 17.14 в /13/);
De - поправка к интегральной степени черноты в случае перекрывания полос, когда в смеси присутствуют СО2 и водяной пар (рисунок17.15 в /13/).
Полное давление смеси: Р=0,202 МПа.
Парциальные давления компонентов смеси:

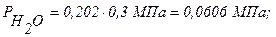

Вычисление параметров:


 ;
;
 .
.
Из рисунка 17.11:  .
.
Из рисунка 17.13:  .
.
Из рисунка 17.12:  .
.
Из рисунка 17.14: 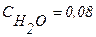 .
.
Из рисунка 17.15:  .
.
Тогда:

Поток излучения Q, падающий на всю поверхность стенок А, определяется выражением:
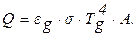
Площадь стенок равна:
А = [2×(0,305 ×0,305)+4×(0,305×1,22)]м2=1,674м2 .
Откуда:

Дата добавления: 2015-12-26; просмотров: 5992;
