Задачи для самостоятельного решения. 3.1 Поверхность Солнца имеет эффективную температуру абсолютно черного тела 5780 К

3.1 Поверхность Солнца имеет эффективную температуру абсолютно черного тела 5780 К. Какой процент энергии излучения Солнца приходится на видимую область спектра (от 0,4 до 0,7 мкм)? Какой процент приходится на ультрафиолетовую область спектра (0,02 – 0,4 мкм)? Каким длине волны и частоте соответствует максимум энергии излучения? Каково максимальное значение полусферической спектральной поверхностной плотности потока излучения?

3.2 Листовое кварцевое стекло пропускает 92% падающего излучения в диапазоне длин волн от 0,35 до 2,7 мкм и в основном непрозрачно для излучения, соответствующего более коротким и более длинным волнам. Какой процент солнечного излучения пропускает стекло? (Принимать Солнце за абсолютно черное тело, имеющее температуру 5780 К). Если растения в оранжерее излучают подобно абсолютно черному телу при 38°C, то какой процент этого излучения пропускает такое стекло?

3.3 Белая керамическая поверхность имеет распределение полусферической спектральной степени черноты при температуре 1667 К, изображенное ниже. Чему равна ее полусферическая интегральная степень черноты?

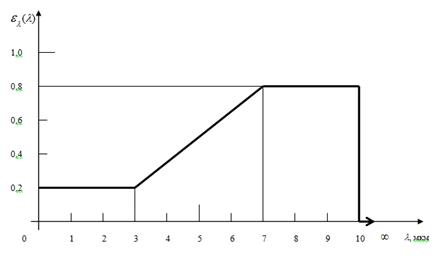
3.4 Поверхность при температуре 333К имеет следующие значения полусферической спектральной степени черноты:

а) Какова полусферическая интегральная степень черноты поверхности при температуре 60°C?

б) Какова полусферическая интегральная поглощательная способность поверхности при температуре 60°C, если источником падающего излучения является серая поверхность (степень черноты 0,8) при температуре 1110 К? Излучение распространяется равномерно при всех углах падения.

3.5 Удельное электрическое сопротивление металлов при температуре 300К равно: 1,65×10^-6 Ом×см для серебра, 11,0×10^-6 Ом×см для платины и
20,8×10^-6 Ом×см для свинца. Каковы теоретические значения полусферической интегральной степени черноты этих металлов и как они согласуются с табличными данными для чистых неокисленных полированных поверхностей?

3.6 Полированная платиновая поверхность поддерживается при температуре Т_А= 222 К. На поверхность падает излучение, испускаемое абсолютно черной полостью, охватывающей эту поверхность при температуре T_i=444 К. Определить полусферически - направленную интегральную отражательную способность в направлении нормали к поверхности.

3.7 На некоторую идеальную селективную поверхность падает по нормали поток излучения, соответствующий по величине среднему значению солнечной постоянной q_i, равной 1394 Вт/м². Тепло к поверхности или от нее передается только излучением. Определить максимальную равновесную температуру Т_равн, соответствующую пороговой длине волны l_с= 1 мкм. (Принять, что спектральное распределение энергии солнечного излучения, падающего на данную поверхность, пропорционально распределению энергии в спектре абсолютно черного тела при температуре 5556 К).

3.8 Используя метод натянутых нитей, вывести выражение для углового коэффициента F_1-2 между бесконечно длинной пластиной и цилиндром, показанными ниже (в сечении).

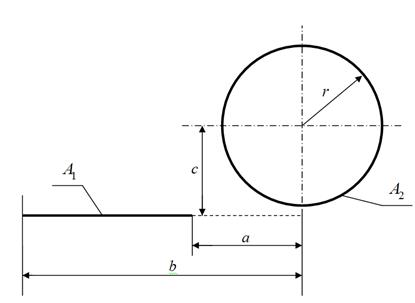
Рисунок

3.9 Заготовка из углеродистой стали размером 1,22´0,61´0,61 м первоначально находится при температуре 1111К и затем поддерживается в таком режиме, что теряет тепло излучением со всей своей поверхности в окружающую среду с температурой 294К (предполагается, что окружающая среда обладает свойствами черного тела). Также предполагается, что теплопроводность стали – бесконечно большая величина. Пренебрегая конвективными тепловыми потерями и предполагая, что заготовка излучает как черное тело, определить, сколько времени потребуется, чтобы заготовка остыла до 555К. Удельная теплоемкость стали
с_р=0,67 кДж/кг×град.

3.10 Определить результирующий тепловой поток с 1м длины при теплообмене излучением между двумя бесконечными параллельными полосами, расстояние между которыми h₁= 3 м. Ширина полос одинакова а₁ = а₂ = 2 м. Интегральная степень черноты полос e₁= e₂ = 0,8, а температуры их поверхностей
t₁ = 500°C и t₂=200°C. Как изменяется угловой коэффициент и тепловой поток, если полосы установить на расстоянии h₂ =1,5 м и h₂ =6 м? Построить графические зависимости значений угловых коэффициентов и тепловых потерь от расстояния между полосами.

3.11 Каково влияние одного тонкого экрана на поток результирующего излучения между двумя концентрическими сферами? Предполагаем, что поверхности сферы и экрана диффузионно-серые со степенями черноты, не зависящими от температуры. Обе стороны экрана имеют одинаковую степень черноты e_s, а внутренняя и наружная сферы имеют соответственно степени черноты e₁ и e₂.

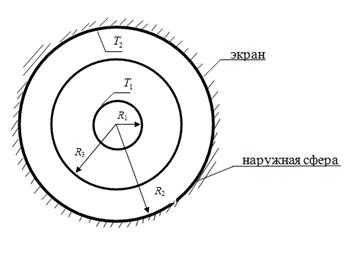
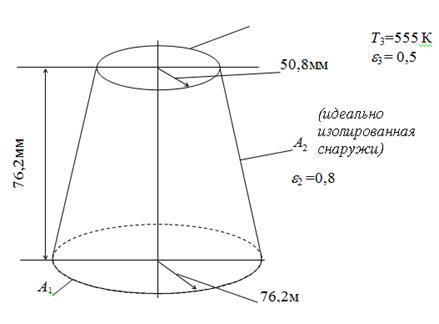
3.12 К нижнему основанию усеченного конуса подводится тепло, как показано на рисунке. Верхнее основание поддерживается при температуре 555 К, а боковая поверхность идеально изолирована. Все поверхности диффузно-серые. Какова температура поверхности 1 в результате теплообмена излучением внутри замкнутой системы? (Для простоты не делить поверхность на участки.)

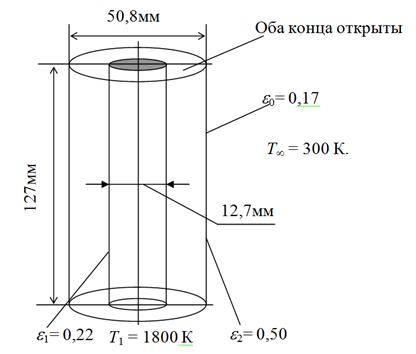
3.13 Стержень диаметром 12,7 мм и длиной 127 мм находится при температуре Т₁ = 1800 К и имеет интегральную степень черноты e₁= 0,22. Стержень расположен внутри тонкостенного концентрического цилиндра диаметром 50,8 мм и той же длины. Степень черноты внутренней поверхности цилиндра e₂= 0,50, а наружной e₀= 0,17. Все поверхности серые. Система подвешена в большой вакуумной камере, где Т_¥ = 300 К. Какова температура Т₂ цилиндрической оболочки? ( Для простоты не делить поверхность на участки. Указание: F_2-1=0,225,
F_2-2=0,617.)

3.14 Пучок монохроматического излучения с длиной волны l = 2,5 мкм и интенсивностью 9462 Вт/м²×мкм падает на слой газа толщиной 0,203 м. Газ имеет температуру 1110 К, его коэффициент поглощения равен
а_{2,5 мкм}=6,56 м^-1. Какова интенсивность пучка на выходе из слоя газа? Пренебречь рассеянием, но учесть собственное излучение.

3.15 Излучение с длиной волны 1,5 мкм проходит через газ с температурой 10000К. Каково отношение истинного коэффициента поглощения к коэффициенту поглощения?

3.16 Внутренний объем печи имеет форму куба с размером ребра 0,61м и заполнен смесью СО₂ и N₂ в соотношении 1 : 1 . Температура газа постоянна и равна 1670 К, а стенки охлаждены до 1110 К. Внутренние поверхности стенок черные. Какой поток результирующего излучения, подводимого к газу (и снимаемого со стенок), необходим для сохранения этих температур?