Основные теоретические сведения. Ранее были рассмотрены условия распространения тепла при стационарном режиме, когда температурное поле во времени не менялось

Ранее были рассмотрены условия распространения тепла при стационарном режиме, когда температурное поле во времени не менялось, оставаясь постоянным. Такие процессы теплопроводности, когда поле температуры в теле изменяется не только в пространстве, но и во времени, называются нестационарными.

Среди практических задач нестационарной теплопроводности важное значение имеют две группы процессов:

а) тело стремится к тепловому равновесию;

б) температура тела претерпевает периодические изменения.

К первой группе относятся процессы нагрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием.

Ко второй группе относятся процессы в периодически действующих подогревателях.

В условиях передачи тепла через стенку при внезапном изменении температуры одного из теплоносителей не все тепло будет передаваться через стенку: часть его уйдет на изменение внутренней энергии самой стенки (ее температуры), и только при наступлении стационарного процесса все тепло будет передаваться через стенку от одной жидкости к другой.

При внесении тела в среду с постоянной температурой по мере нагрева (охлаждения тела) температура в каждой точке тела будет асимптотически приближаться по времени к температуре окружающей среды.

Эти примеры указывают на то, что нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества. Так как скорость изменения энтальпии прямо пропорциональна способности материала проводить тепло (т.е. коэффициенту теплопроводности λ) и обратно пропорциональна его аккумулирующей способности (т.е. объемной теплоемкости с_ρ ), то в целом скорость теплового процесса при нестационарном режиме теплопроводности определяется значением коэффициента температуропроводности 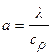, который здесь имеет такое же важное значение, как и коэффициент теплопроводности при стационарном режиме распространения тепла.

Рассмотрим лишь несколько важных задач, относящихся к процессам, в которых тело стремится к тепловому равновесию. Для более широкого ознакомления с решениями большого круга задач нестационарной теплопроводности как в случаях стремления температуры тела к состоянию равновесия, так и ее периодического изменения, следует обратиться к специальной литературе /2, 4, 10, 14, 15, 21-28, 30, 32, 33/.Ниже в таблице приведены постановка и решения задач нестационарной теплопроводности для полуограниченного тела (задачи 1-3), неограниченной пластины (задачи 4-9), неограниченного цилиндра (задачи 10-12) и шара (задачи 13-15).

Дифференциальные уравнения теплопроводности в предложенных задачах имеют вид:

для полуограниченного тела и неограниченной плоской пластины:

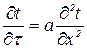; (4.1)

для неограниченного цилиндра:

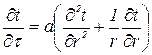; (4.2)

для шара:

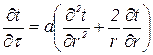. (4.3)

В выражениях (4.1 ÷ 4.3) t – температура тела, x, r – координаты распространения тепла, τ – время процесса. Условия однозначности, тепловые схемы и решения задач в критериальном виде приведены также в этой таблице.

Относительно решения задач нестационарной теплопроводности следует отметить, что после выбора тепловой схемы задачи и назначения начальных и граничных условий требуемая задача может быть решена аналитически (или графически /30/) по предложенным выражениям.

В полученных решениях критерий Фурье 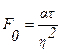представляет собой относительное безразмерное время процесса. В нем сопоставлено текущее время τ и группа величин 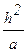, имеющая размерность времени и характеризующая скорость перестройки температурного поля в теле. Отношение 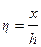является безразмерной координатой.

В задачах с граничными условиями третьего рода, кроме Fo и h , добавляется еще одна независимая переменная – критерий Био 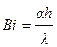. Здесь a –коэффициент теплообмена внешней среды и тела, λ - коэффициент теплопроводности тела, h – определяющий размер тела: для пластины - толщина, для полуограниченного тела – глубина и т.д. Отношение внутреннего и внешнего тепловых сопротивлений, соответственно 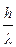и , называется критерием Вi:

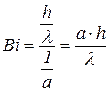. (4.4)